1.4. Общие замечания об измерении информации

1. Возможно большое количество определения и способов измерения информации.

2. Во всех определениях имеет место оценка неопределенности, неожиданности, многообразия, характеризуемая либо вероятностью, либо какой-либо другой мерой сложности.

3. Современные меры информации в значительной мере опираются на субъективные предпосылки.

4. После формализации понятия информации появляется возможность ее использования в ситуациях, для которых понятие информации по человеческим понятиям неприменимо. Это объясняется тем, что теория информации – математическая дисциплина и, например, физическое содержание вероятности в теории Шеннона в принципе может быть любым.

5. Вводимые определения информации могут быть беднее по смыслу того, что имеет в виду человек.

1.5. Энтропия непрерывных сообщений

Исходные данные часто представляются в виде непрерывных величин, например, температура воздуха или морской воды. Поэтому представляет интерес измерение количества содержащейся в таких сообщениях информации.

Как было сообщено выше, средняя энтропия дискретного сообщения, входящего в полную группу из m независимых сообщений, находится по формуле: .

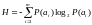Эта формула справедлива, в частности, для сообщений, состоящих из конечного числа букв (в нашем случае m штук).

Если рассматривать попадание значения непрерывного сообщения в определенный интервал, как появление определенной буквы, то непрерывное сообщение можно рассматривать как предельный случай дискретного если число букв устремить к бесконечности (рис. 1.3).

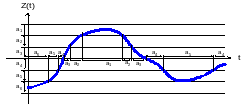
Рис. 1.3. Представление непрерывного процесса в виде дискретной последовательности букв.

Для вычисления энтропии дискретного сообщения необходимо было знать множество букв и вероятности их появления. Аналогом набора вероятностей букв в непрерывном сообщении является плотность вероятностей f(a) распределения значений непрерывного сообщения (рис. 1.4).

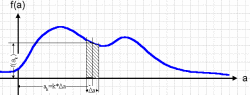
Рис. 1.4. Вычисление вероятности попадания значений непрерывного процесса в некоторый интервал шириной ∆a.

Непрерывную величину можно считать предельным случаем квантованной по уровню, если размер шага квантования ∆a устремить к нулю.

Зная плотность распределения вероятности (дифференциальный закон распределения) и предполагая независимость соседних значений случайной величины, можно найти, используя известную формулу, среднюю энтропию одного ее значения:

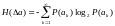, где a_k=k*∆a

Из теории вероятностей известно, что вероятность попадания случайной величины в некоторый интервал находится через дифференциальный закон ее распределения по формуле:

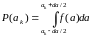
При достаточно гладкой функции P(a) и малом ∆a можно считать, что

.

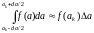Поэтому

.

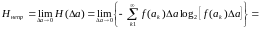
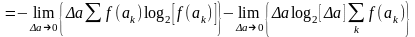Первое слагаемое в пределе превращается в интеграл:

.

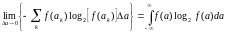Во втором слагаемом тоже образуется интеграл. Это определенный интеграл от дифференциального закона распределения с бесконечными пределами, который, как известно, равен 1. В результате получаем:

.

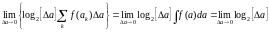Ясно теперь, что первое слагаемое – конечное число, а второе - бесконечное. Как и следовало ожидать, энтропия непрерывного сообщения в математическом смысле бесконечно велика, что означает, что непрерывный сигнал несет в себе бесконечно большое количество шенноновской информации. Однако в реальной жизни это не так. Любое непрерывное сообщение, например показания термометра за окном или пружинных весов, человек так или иначе подвергает квантованию, что приводит к уменьшению количества информации по шеннону.

Таким образом, в математическом смысле непрерывные сигналы-сообщения не имеют абсолютной меры энтропии. Поэтому для них вводится понятие относительной энтропии. Это понятие подразумевает наличие эталона, с которым сравнивается энтропия непрерывного сообщения. В качестве такого эталона выбирается также непрерывное сообщение-сигнал, имеющий равномерный закон распределения в интервале ε (эпсилон). График равномерного закона приведен на рис. 1.5.

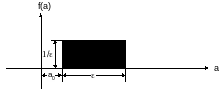
Рис. 1.5. График равномерного закона распределения.

Абсолютная энтропия такого эталонного сообщения равна:

.

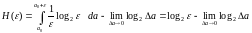Из-за второго члена H(ε) также бесконечно велика.

Относительная энтропия непрерывного сообщения в данном случае определяется как разность между абсолютной энтропией H_непр этого сообщения и абсолютной энтропией H(ε) эталонного сообщения. Ее принято называть дифференциальной эпсилон-энтропией непрерывного сообщения. Она обозначается H_ε и вычисляется по формуле:

.

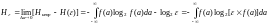Если положить ε=1, то дифференциальная энтропия (слово эпсилон часто не произносится) запишется в виде:

.

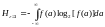Видим, что формула дифференциальной энтропии похожа на формулу энтропии дискретного источника, но следует помнить, что она описывает не абсолютное, а относительное значение энтропии, когда за стандарт взята случайная величина, равномерно распределенная на единичном интервале.

Дифференциальная энтропия позволяет сравнивать различные непрерывные источники сообщений по степени информативности.