I. Теоретические вопросы:

Представление данных в виде числовых массивов.

Алгоритмы обработки числовых массивов.

Представление массивов в памяти компьютера.

Действия над матрицами.

Практическое значение матричного представления данных.

II. Задачи для самостоятельного решения:

1. Даны матрицы А и В размера k×m и m×l соответственно. Найти произведение АВ.

2. Дана квадратная матрица порядка n. Получить матрицу А².

3. Даны квадратные матрицы Аи В порядка n. Получить матрицу АВ-ВА.

4. Дана квадратная матрица А порядка n. Получить матрицу АВ; элементы матрицы В вычисляются по формуле:

а) ;

б)

в)

(i, j = 1, …, n).

5. Даны квадратная матрица А порядка n и вектор b с n элементами. Получить вектор:

а) ;

б) ;

в) где Е – единичная матрица порядка n.

6. Дана квадратная матрица А порядка n. Получить вектор , где b – вектор, элементы которого вычисляются по формуле:

а) ;

б)

(i = 1, …, n).

7. Даны квадратная матрица А порядка n, векторы x и y с n элементами. Получить вектор .

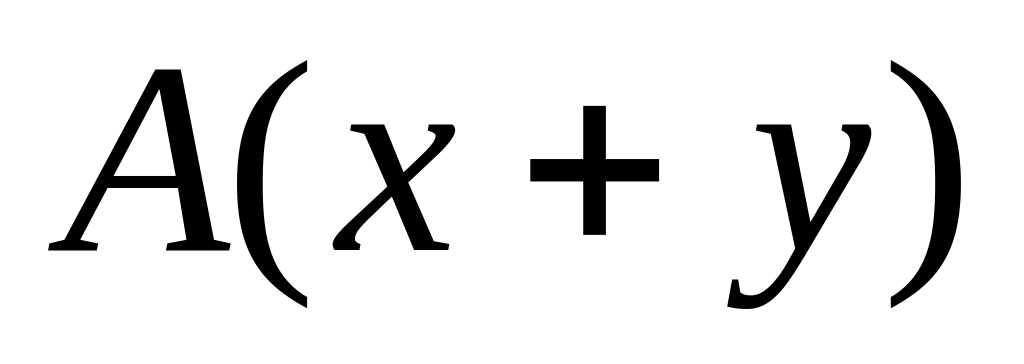8. Даны квадратные матрицы А, В и С порядка n. Получить матрицу .

9. Даны квадратные матрицы А и В порядка n. Получить матрицу , где Е – единичная матрица порядка n, а элементы матрицы С вычисляются по формуле

.

10. Пусть даны квадратная матрица А порядка m и натуральное число n; требуется найти 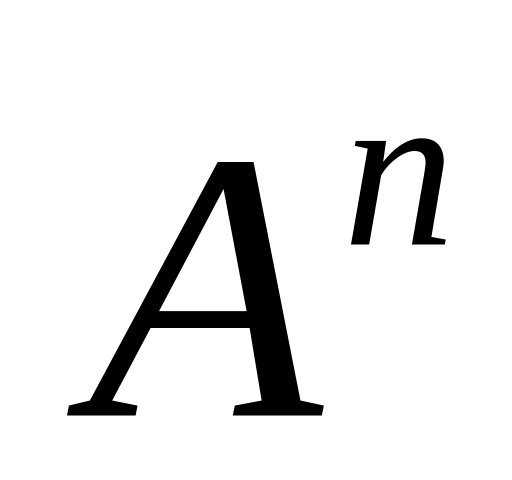. Алгоритм, основанный на непосредственном применении формулы 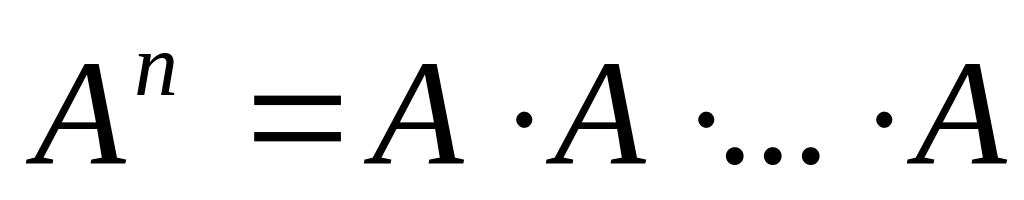(n сомножителей), слишком разорителен. Например, экономичнее вычислять как 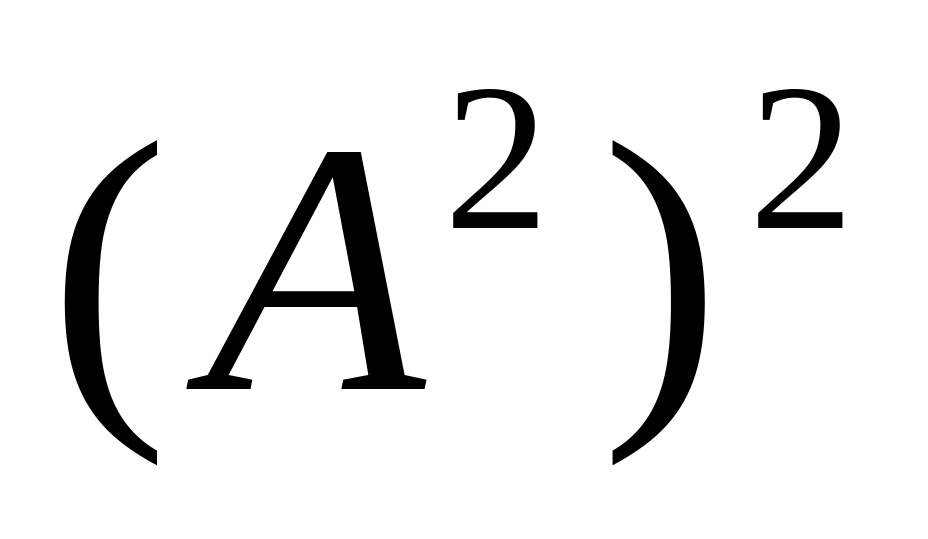. Идея одного достаточно экономного алгоритма вычисления заключена в следующем: если , то 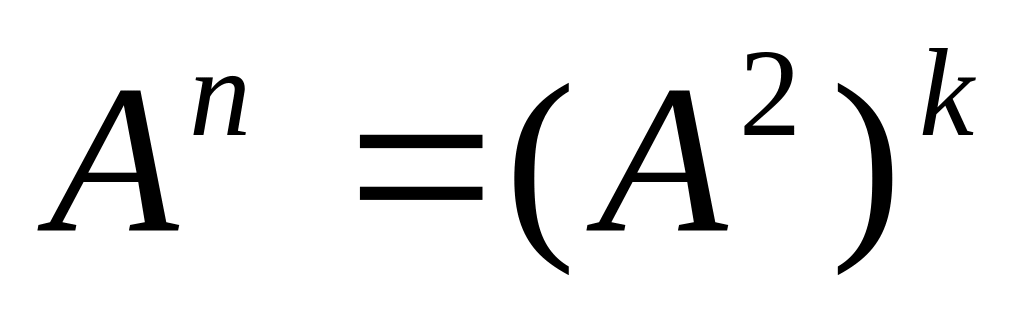, если же 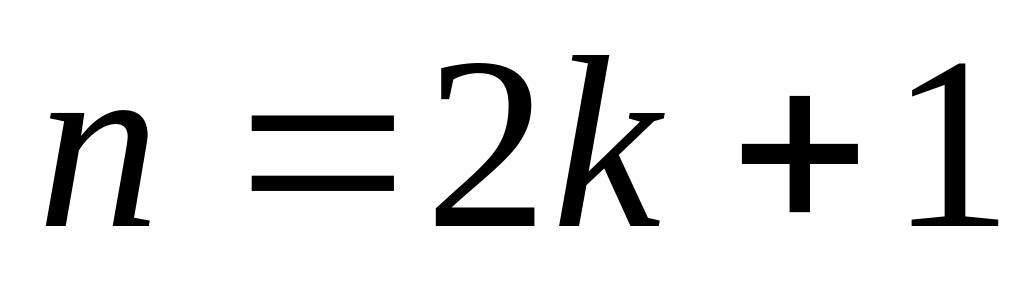, то 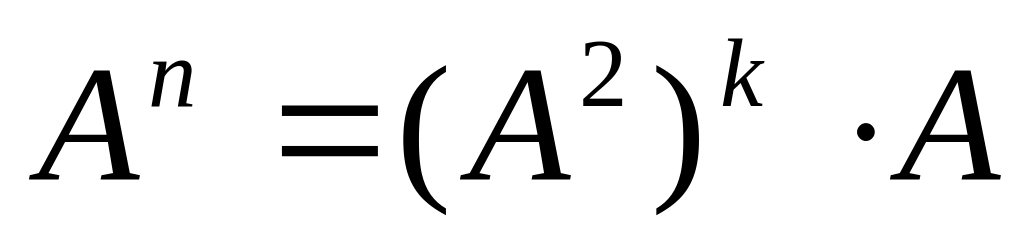. Степень с показателем k вычисляется с учётом этих же соображений. Итак, надо разделить n на 2 с остатком: 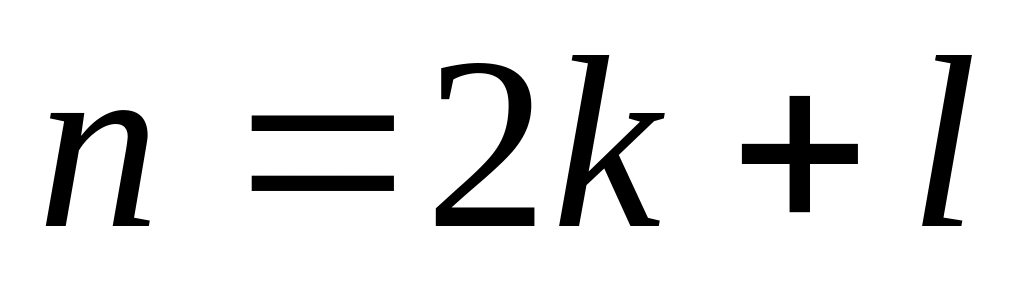(0≤l≤1), потом это же проделать с k и т. д. Эти действия приводят, как известно, к построению двоичной записи n. Алгоритм, основанный на этой идее, состоит в том, что последовательно вычисляются 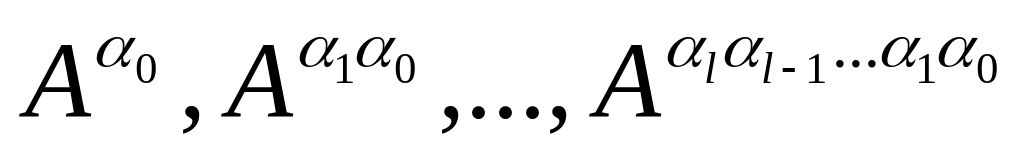, где 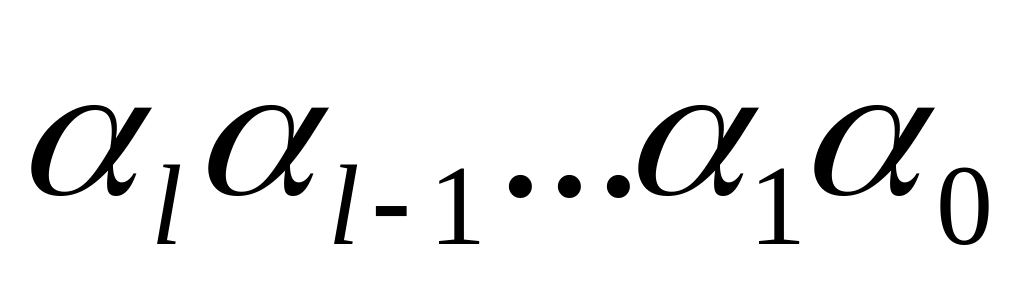- двоичная запись числа n. Для этого вычисляется, цифра за цифрой, двоичная запись n и, параллельно, степень за степенью, - каждая следующая степень получается из предыдущей возведением в квадрат. Подсчитывается произведение тех из вычисленных степеней, для которых соответствующая цифра двоичного представления равна 1. Например, запись 9 в двоичной системе есть 1001 (9 = 1 8+0 4 + 0 2+ 1); для вычисления доста­точно найти , , (3 умножения), а затем определить 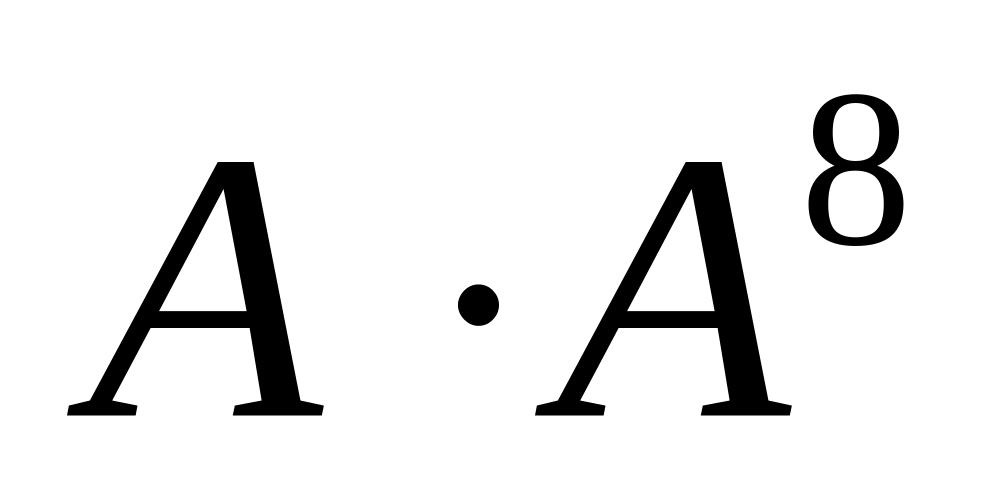(1 умножение). Преимущество этого алгоритма в сравнении с простейшим состоит в том, что простейший алгоритм требует числа умножений, растущего как линейная функция от n, а здесь число умножений, грубо говоря, пропорционально количеству цифр числа n или двоичному логарифму n. Это преимущество весьма ощутимо при работе с матрицами (из-за трудоемкости каждого умножения), хотя, разумеется, этот алгоритм может быть использован и для вычисления степени любого числа.

Написать программу, реализующую предложенный алгоритм.

11. Дана квадратная матрица А порядка 5. Получить матрицу (см. предыдущую задачу).

12. Дана матрица А размера m×n. Получить транспонированную матрицу (её размер n×m).

13. Дана матрица А:

а) размера m×m;

б) размера m×n.

14. Дана квадратная матрица А порядка m. Получить матрицы и .

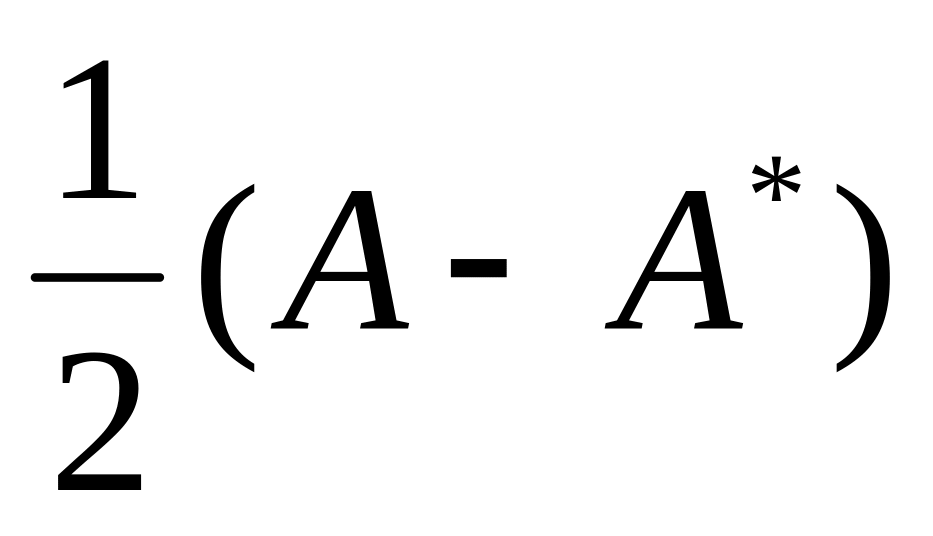15. Следом квадратной матрицы называется сумма элементов, расположенных на главной диагонали.

Даны квадратная матрица порядка m, натуральное число n. Вычислить следы матриц .

16. Комплексная матрица Z представляется парой X, Y действительных матриц так, что . Даны действительные квадратные матрицы A, B, C и D порядка m. Найти произведение двух комплексных матриц и 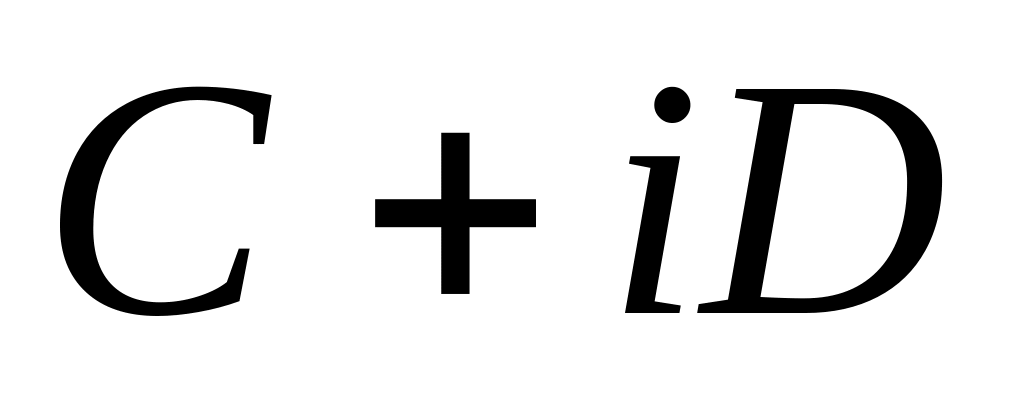, т.е. найти действительные квадратные матрицы X и Y порядка m такие, что .

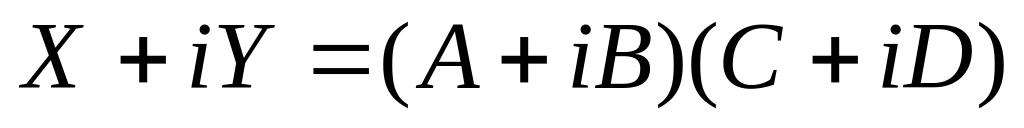17. Пусть для квадратной матрицы А, имеющей порядок n, существует обратная матрица 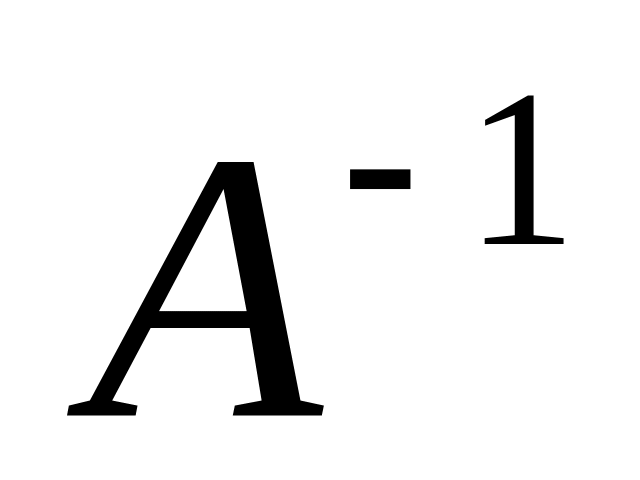. Тогда, рассматривая элементы матрицы как неизвестные величины, из соотношения 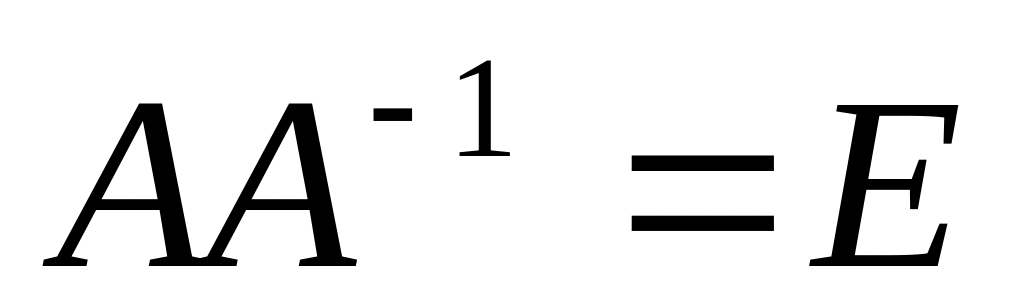, где Е-единичная матрица порядка n, можно получить систему 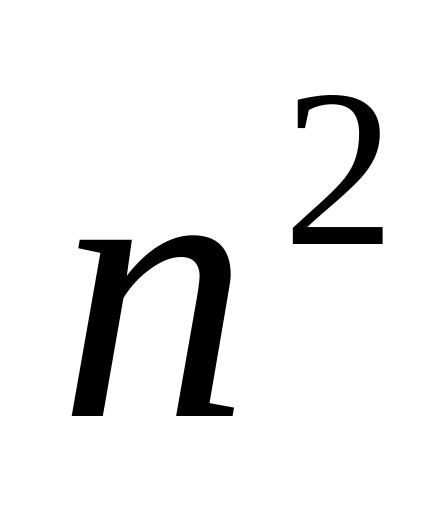линейных уравнений с неизвестными. Найти матрицу этой системы и вектор, определяющий её правую часть, считая, что неизвестные элементы матрицы пронумерованы так, что сначала по порядку идут элементы первой строки, затем – второй и т.д. Считать, что А- заданная матрица порядка 4; в ответе должны получиться квадратная матрица и вектор порядка 16.

18. Симметричная квадратная матрица А порядка n задана последовательностью чисел, аналогично правой треугольной матрице (см. задача 20). Кроме этой последовательности дан вектор b с n элементами. Найти вектор Ab.

19. Симметричные квадратные матрицы А и В порядка n заданы последовательностями из чисел, аналогично правым треугольным матрицам (см. задача 20). Получить в аналогичном виде:

а) матрицу АВ;

б) матрицу .