Раздел 3. Многочлены.

I. Теоретические вопросы:

Операторы языка С/С++, используемые для организации основных структур алгоритмов

Вычисление степенного полинома явным образом.

Вычисление степенного полинома по схеме Горнера.

Вычисление производных от функций, представленных в виде степенных полиномов.

Действия над многочленами.

II. Задачи для самостоятельного решения:

1. Дан многочлен¹ степени n. Получить многочлен .

2. Дан многочлен степени n. Получить многочлен . (Какова степень этого многочлена?)

3. Дан многочлен степени n. Получить его производную , а также вычислить , , .

4. Даны действительное число а, многочлен степени n. Получить:

5. а) многочлен ;

6. б) многочлен ;

7. в) многочлен .

8. Даны действительные числа s и t, натуральное число n, действительные числа Среди есть как отрицательные, так и неотрицательные числа. Получить значение P(s)+Q(t), где в качестве коэффициента многочлена Р взяты отрицательные члены поеледовательности (с сохранением порядка их следования), а в качестве коэффициентов многочлена Q-неотрицательные члены (также с сохранением порядка их следования).

9. Даны действительные числа s, t, многочлен Р(х) степени n. Найти значение .

10. Даны действительные числа s, t, многочлен Р(х) степени n. Получить многочлен , где - производная многочлена Р(х).

11. Даны действительные числа Получить многочлен шестой степени .

12. Даны действительные числа , . Получить многочлен шестой степени .

13. Даны действительные числа , многочлен Р(х) шестой степени. Получить действительные числа такие, что .

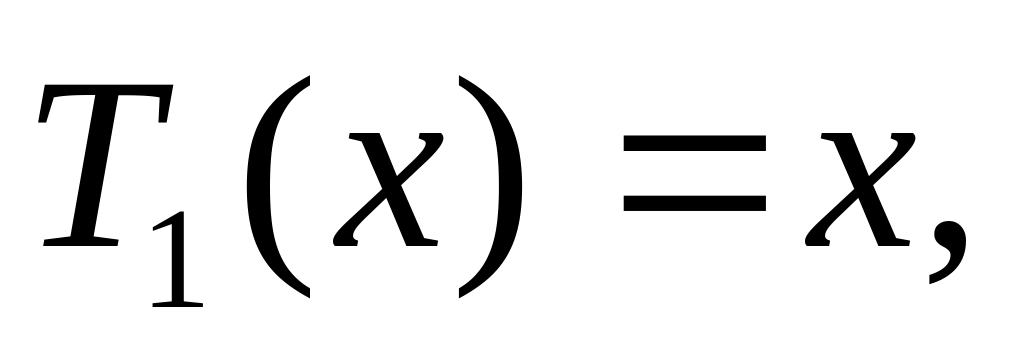
14. Последовательность многочленов … определяется следующим образом: . Получить …, .

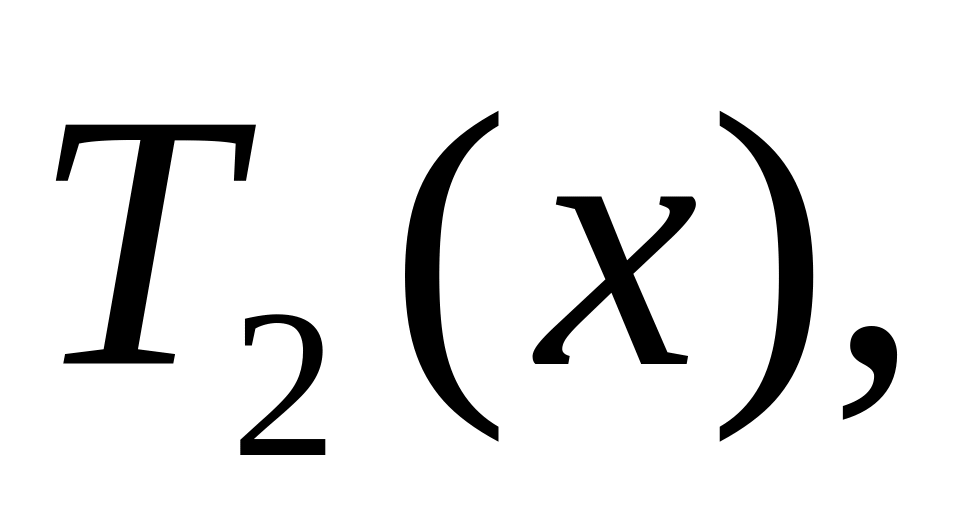15. Последовательность многочленов … определяется следующим образом: .

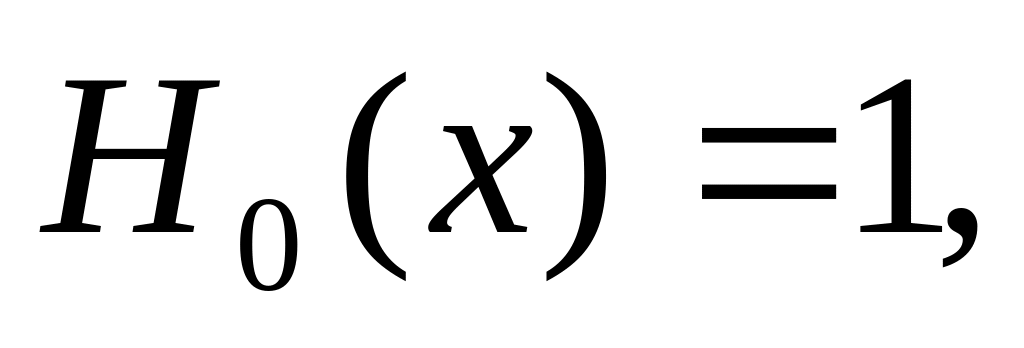
а) Получить ;

б) Даны действительные числа . Получить многочлен .

в) Дано действительное число а. Вычислить .

16. Последовательность многочленов … определяется следующим образом:

. Выполнить для , , … задания а), б), в), сформулированные в предыдущей задаче для многочленов .

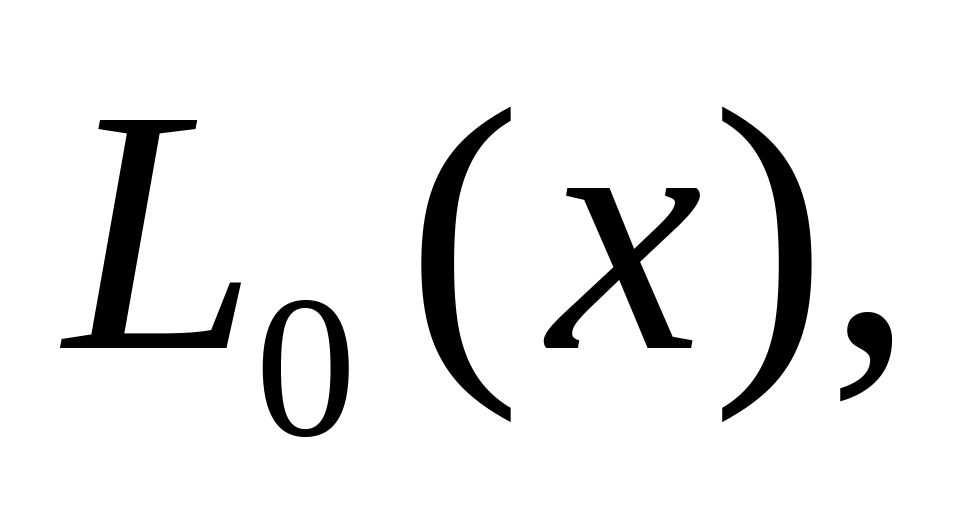
17. Последовательность многочленов … определяется следующим образом:

а) Получить ;

б) Даны действительные числа . Вычислить .

в) Получить многочлен .

18. Даны действительные числа , . ( попарно различны). Требуется найти многочлен F(x) степени не выше, чем n, такой, что 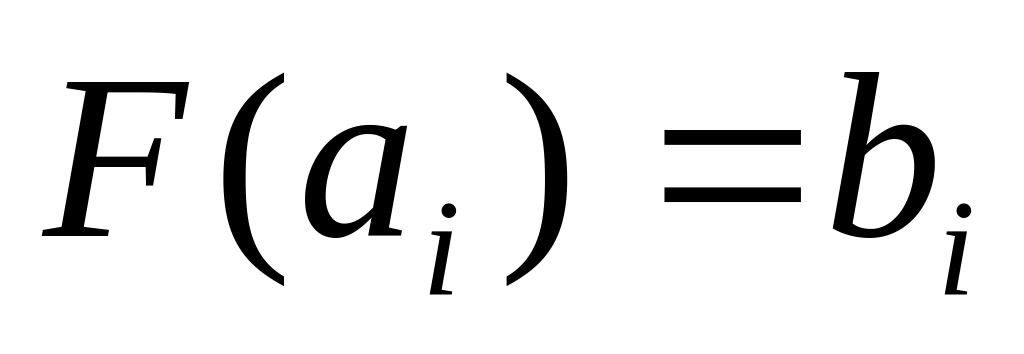(i=0,1,…,n).

Отметим, что нетрудно построить многочлены , каждый из которых имеет степень n и которые обладают тем свойством, что равен 1 при и равен 0 при - для этого достаточно положить ,

В качестве искомого многочлена F(x) берётся сумма .

Раздел 4. Преобразование и построение матриц.

1. Теоретические вопросы:

Обработка числовых массивов.

Виды массивов.

Представление массивов в памяти компьютера.

Практическое значение организации данных в виде матриц.