5.1. Программные модели автоматов

В предыдущей главе рассмотрены различные алгоритмические модели

автоматов. После выбора алгоритмической модели начинается этап собственно

программной реализации, первая стадия которой — выбор языка

программирования. Предположим, что в качестве такого языка выбран

язык СИ, весьма удобный при реализации СБФ, так как он наряду с

логическими операторами содержит также и поразрядные логические

операторы. Ниже будет показано, что этот язык также удобен и для

реализации ГП.

Под программной моделью будем понимать программу и совокупность

операторов, используемых в ней при реализации алгоритмической модели

в рамках выбранного языка программирования.

Так, например, если в качестве алгоритмической модели выбрана

СБФ, то одна программная модель может базироваться на поразрядных

логических операторах И, ИЛИ, НЕРАВНОЗНАЧНОСТЬ, ДОПОЛНЕНИЕ,

а другая — на логических операторах И, ИЛИ, НЕ.

Аналогичная ситуация возникает также и при использовании ГСА в

зависимости от того, применяется ли оператор условия или условный

оператор.

По аналогии с алгоритмическими моделями существуют и программные

модели второго порядка — модели реализации в базисе языка

ассемблера. Так, например, при использовании в записи булевой формулы

поразрядных операторов трансляция осуществляется в операторные ассемблерные

программы, а при использовании логических операторов —

в бинарные ассемблерные программы [88].

Автором совместно с В. Н. Кондратьевым выполнено сравнение по

памяти команд и быстродействию более 60 программ в базисе языка СИ,

реализующих (разными методами и операторами) функцию «голосование

два и более из трех», и более 25 программ, реализующих СБФ, описывающую

одноразрядный сумматор. При этом необходимо отметить, что

полученные результаты для одного и того же алгоритма могут отличаться

вплоть до десятков раз (Приложения 1, 2).

152

Из изложенного в разд. 2.3 следует, что в качестве языка спецификаций

автоматов с памятью наиболее целесообразно использовать ГП. При

переходе к алгоритмическим моделям графы переходов естественно

сохранить. Поэтому и в качестве программной модели автоматов с

памятью целесообразно выбрать такую конструкцию, которая позволяет

изоморфно отразить в ней ГП. Такой моделью является конструкция

s w i t c h языка СИ, используемая в виде аналогов в большинстве языков

программирования высокого уровня.

В рамках применения конструкции s w i t c h в свою очередь возможна

многовариантность, определяемая числом таких конструкций (одна или

две), выбранной структурной моделью автомата, учитывающей в том числе

и его род, и способом реализации булевых формул.

Вопрос о независимой или совместной реализации булевых формул,

входящих в конструкцию switch, может решаться как при выборе

структурной модели автомата, так и при построении его программной

модели.

В любом случае эти формулы могут быть реализованы и оптимизированы

либо независимо в каждом операторе if, либо совместно для всех

этих операторов после выноса формул, содержащих более одной буквы,

из конструкции switch.

Оптимизация формул может выполняться и в рамках каждой метки

c a s e 1 за счет изменения порядка проверки. Так, например, эквивалентны

конструкции:

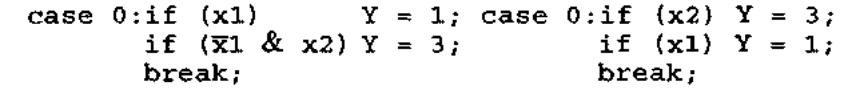
булевы формулы в которых обладают разной сложностью.

Кодирование состояний автоматов

При построении графа переходов каждой вершине (состоянию) присваивается

номер — некоторое целое десятичное положительное число.

Принудительное кодирование. Если во всех состояниях ГП коды

выходных переменных различаются, то каждое число, обозначающее

номер состояния, может быть закодировано двоичным вектором, совпадающим

с вектором значений выходных переменных в этом состоянии.

Такой вид кодирования будем называть «принудительным». Структурная

модель автомата, использующего этот вид кодирования, соответствует

автомату без выходного преобразователя. Однако если в ГП в различных

состояниях должны формироваться одинаковые значения выходных переменных,

то при использовании этого вида кодирования такой ГП

автоматом указанного типа не может быть реализован.

Принудительно-свободное кодирование. Универсальность автомата

без выходного преобразователя при реализации ГП, в которых векторы

значений выходных переменных совпадают в некоторых состояниях,

обеспечивается принудительно-свободным кодированием состояний.

Кодирование в этом случае осуществляется следующим образом:

разряды принудительной части вектора каждого состояния совпадают со

значениями выходных переменных рассматриваемого состояния, а количество

разрядов в свободной части вектора равно двоичному логарифму

числа состояний, в которых выходные векторы совпадают. Значения

разрядов в свободной части кодов состояний, в которых значения выходных

переменных совпадают, должны различаться между собой, а для

остальных состояний выбор свободной части векторов произволен. Пусть,

например, автомат с тремя состояниями имеет следующие векторы зна-

5* 67

чений выходных переменных: 00, 01, 01. Они образуют принудительную

часть векторов состояний. В данном случае в двух состояниях значения

выходных переменных совпадают и поэтому в свободной части векторов

достаточно иметь log22 = 1 разряд, различающий эти состояния. Таким

образом, может использоваться один из следующих вариантов кодирования:

00*, 010, 011 или 00*, 011, 010, где * — символ, обозначающий

произвольное значение двоичного разряда. Этот вид кодирования обеспечивает

универсальность автомата без выходного преобразователя.

Разновидности свободного кодирования. Если автомат содержит

выходной преобразователь, как это имеет место, например, в автоматах

Мура, то векторы кодов состояний автомата могут выбираться независимо

(свободно) от векторов значений выходных переменных, так как именно

с помощью этого преобразователя и может быть осуществлено перекодирование

произвольного вектора состояния в требуемый вектор выходных

переменных.

Свобода кодирования во многом связана с программной реализацией

алгоритмов, так как в данном случае в отличие от схем в применении

противогоночных или помехоустойчивых кодов [27] нет необходимости.

Рассмотрим четыре вида кодирования, которые будем использовать

для автоматов с выходным преобразователем: логарифмическое, унитарное

(единичное), двоичное и многозначное.

Логарифмическое кодирование. Если десятичный номер каждого

состояния закодировать числом, равным двоичному эквиваленту номера,

или сопоставить десятичному номеру некоторое двоичное число, количество

разрядов которого равно ]log2s[ (где s — число состояний автомата;

] [ — символ округления до ближайшего большего целого), то такой

вид кодирования называется логарифмическим кодированием.

Унитарное (единичное) кодирование. При использовании унитарного

кодирования в его классической трактовке [13] i-й вершине сопоставляется

5-местный вектор, в котором только на i-й позиции размещается

единица, а на остальных позициях — нули.

Двоичное кодирование. Присвоим i-й вершине ГП только одну

переменную Yi. Эта переменная равна единице в случае, когда автомат

находится в этой вершине, и нулю — в противном случае.

Такой вид кодирования связан с присвоением каждому состоянию

2s - 1 векторов, каждый из которых s-местный, причем различным состояниям

присваиваются в том числе и одинаковые векторы. В этом случае,

как и в предыдущем, рабочими являются векторы с одной единицей, в то

время как все остальные векторы рабочими не являются.

Наличие только одной единицы в каждом рабочем векторе является

признаком для обнаружения факта перехода автомата в нерабочее состояние,

что невозможно при логарифмическом кодировании. Этот вид

кодирования обеспечивает построение весьма простых булевых формул,

бесповторных по переменным состояний.

Многозначное кодирование. Если в качестве кода i-го состояния

использовать десятичный номер, присвоенный i-й вершине ГП, то это

означает, что в автомате используется многозначное кодирование, т. е.

все состояния автомата кодируются одной переменной Y, которая может

принимать s значений. Алгоритмические модели автоматов

После выбора структурной модели автомата, вида кодирования его

состояний, построения соответствующего графа переходов и анализа его

поведения, например с помощью графа достижимых маркировок, возникает

вопрос о выборе и построении алгоритмической модели, реализующей

этот граф.

В настоящей работе рассматриваются следующие алгоритмические

модели: СБФ, ФС, ГСА, ГП и матрицы переходов.

При этом необходимо отметить, что принятый вариант кодирования

ограничивает разновидности алгоритмических моделей, которые при этом

можно применять. Так, например, при многозначном кодировании булевы

формулы не могут быть использованы.

4.1. Системы булевых формул (СБФ)

4.1.1. Построение СБФ при логарифмическом кодировании

Рассмотрим метод построения формул переходов и выходов при

использовании логарифмического кодирования.

В этом случае число формул переходов равно ]log2s[, а число формул

выходов равно числу выходов М. Получающиеся в этом случае формулы

в дизъюнктивной нормальной форме весьма сложны, так как каждая

конъюнкция содержит все переменные, кодирующие состояния, а каждая

из этих переменных входит в формулу одновременно как в прямой, так

и инверсной форме. Это приводит к повторности булевых формул по этим

переменным, в общем случае мало уменьшающейся даже после вынесения

повторяющихся переменных за скобки.

Формулы переходов для каждой переменной, кодирующей состояния,

строятся отдельно. Для построения такой формулы для переменной уi-

необходимо выделить все вершины, в которых эта переменная закодирована

единицей, и построить дизъюнкцию (по всем этим вершинам)

конъюнкций, каждая из которых состоит из формулы, помечающей дугу

(петлю), входящую в вершину с уi= 1, и конъюкции, соответствующей

коду вершины, из которой исходит указанная дуга (петля).

69

Формула для каждого из выходов строится отдельно. Для автоматов

Мура для переменной zj формула выходов является дизъюнкцией (по всем

вершинам, в которых zj = 1), состоящей из конъюкций, соответствующих

кодам состояний указанных вершин.

Для автоматов Мили формула выходов является дизъюнкцией (по всем

дугам (петлям), на которых zj = 1), включающей в себя конъюнкции,

каждая из которых состоит из формулы, помечающей рассматриваемую

дугу (петлю), и конъюнкции, соответствующей коду вершины, из которой

исходит указанная дуга (петля).

5.1.1. Применение конструкции switch

Изоморфизм ГП и текста программы при использовании конструкции

s w i t c h при отсутствии жестких ограничений на объем памяти и быстродействие

является в большинстве случаев определяющим для применения

пентады (состояние—независимость от глубокой предыстории—

система взаимосвязанных ГП—-многозначное кодирование—конструкция

switch) в качестве основы технологии программной реализации алгоритмов

логического управления по крайней мере на стадии их моделирования.

Использование указанной пентады позволяет обеспечить также и

структурированность программ. Это является принципиальным положением,

так как вопрос о структурировании программ весьма сложен.

В [103] в качестве наилучшего средства структуризации предлагается

использовать алгоритмическую конструкцию, близкую к конструкции

switch, однако не непосредственно, как в настоящей работе, а с целью

объединения отдельных фрагментов в исходной неструктурированной

ГСА. Предлагаемый в настоящей работе подход позволяет отказаться от