Спеціальні коди комп'ютерної схемотехніки

Існує цілий ряд інших двійкових кодів, які мають певні корисні власти­вості і використовуються в різних галузях цифрової техніки

Наприклад код Грея використовується в еле­ктромеханічних аналого-цифрових перетворю­вачах, а також в оптичних і магнітних дискових накопичувачах.

При перетворенні кута повороту диску в двійковий код виникає ситуація, коли можливі великі помилки зв'язані з тим, що при переході між двома сусідніми за значенням числами змі­нюються зразу декілька двійкових розрядів. На рис. 5.1 зображено кодовий диск призна­чений для перетворення кута повороту в двійковий код.

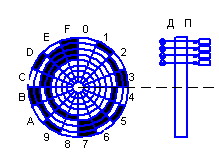
Рисунок 5.1

На диску зроблені віконця у відповідності до значення числа у двійково­му коді, а по різні сторони від нього розташовані джерела світла (Д) і фото­приймачі (П). Системи Д-ГІ називають оптичними парами.

В залежності від кута повороту між оптичними парами буде встановлю­ватись маска того чи іншого двійкового числа.

Недоліком цього способу перетворення є те, що у випадку встановлення диску на границі між двома цифрами, можуть просвічуватись маски двох чисел, особливо фатальною ця похибка буде у випадку коли відрізняються декілька розрядів, наприклад, якщо диск зупиниться між 7 і 8 (0111₍₂₎ і 1000₍₂₎), це може бути сприйнято як чис­ло 15- 1111₍₂₎.

Кодовий диск, світлова маска на якому зроб­лена згідно коду Грея такого недоліку немає. Код Грея формується за таким законом.

1. Старший розряд коду Грея і коду 8421 спів­падає.

2. Кожне наступне число відрізняється тільки в одному розряді починаючи з молодшого.

З рисунку 5.2 видно що ні один перехід між сусідніми числами не змінює більше чим один розряд тобто похибка може бути тільки на одну одиницю.

Таблиця 5.2.1

N	8421	Грея
0	0000	0000
1	0001	0001
2	0010	0011
3	0011	0010
4	0100	0110
5	0100	0111
6	0101	0101
7	0110	0100
8	0111	1100
9	1001	1101
A	1010	1111
B	1011	1110
C	1100	1010
D	1101	1011
E	1110	1001
F	1111	1000

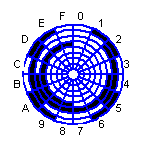
Рисунок 5.2

В таблиці 5.2.2 зібрані деякі двійково-десяткові коди, що використовують в цифровій техніці і си­стемах передачі даних.

Таблиця 5.2.2

N	8421	N+3	4221	Грея	9-N	Джонсона
0	0000	0011	0000	0000	1001	00000
1	0001	0100	0001	0001	1000	00001
2	0010	0101	0010	0011	0111	00011
3	0011	0110	0011	0010	0110	00111
4	0100	0111	1000	0110	0101	01111
5	0101	1000	0111	0111	0100	11111
6	0110	1001	1100	0101	0011	11110
7	0111	1010	1101	0100	0010	11100
8	1000	1011	1110	1100	0001	11000
9	1001	1100	1101	1101	0000	10000

ПОСЛІДОВНІСНІ СХЕМИ .ЛІЧИЛЬНИКИ ІМПУЛЬСІВ .РЕГІСТРИ

Є ряд таких схем, які застосовують у більшості цифрових пристроїв, то­му їх можна вважати типовими функціональними вузлами. Наприклад регі­стри, лічильники, суматори, схеми порівняння, шифратори, генератори ім­пульсів, селектори імпульсів, комірки пам'яті тощо. Ці схеми поділяють на дві великі групи комбінаційні і послідовнісні.

Комбінаційні схеми - це такі схеми стан інформації на виході яких за­лежить тільки від сигналів поданих на входи в даний момент часу, з прихо­дом нової комбінації сигналів вихідний стан визначається тільки нею і не залежить від попередньої.

Послідовнісні схеми - це схеми, стан інформації на виході яких зале­жить не тільки від сигналів поданих на входи в даний момент часу, а і від стану схеми в попередній момент часу (схеми з пам'яттю).

Послідовнісні схеми обов'язково містять тригери. Приклади послідовнісних схем цс лічильники імпульсів, регістри, оперативні запам'ятовуючі пристрої.