Базові положення алгебри логіки

■ Булева алгебра оперує висловлюваннями. Висловлювання, це вираз (фі­зичне явище) що містить певне повідомлення, висловлювання прийнято по­значати літерами англійського алфавіту Х1,Х2,ХЗ_,А,В,С...

• Висловлювання бувають прості і складні (складні висловлювання скла­даються з простих).

• Висловлювання бувають правдиві і помилкові Правдиве висловлювання прийнято позначати "1" помилкове - "0". Наприклад X = 1, X правдиве ви­словлювання.

• Якщо то X=0 . Логічна (булева, двійкова) змінна це довільна фізи­чна величина, що може приймати тільки два значення 0 або 1.

• Складні висловлювання з'єднують з простих з допомогою логічних фун­кцій І, АБО, НЕ.

Способи представлення логічних функцій:

Логічна ( булева, двійкова, перемикальна ) функція - функція від двій­кових аргументів, що також може приймати значення тільки 0 та 1. Існують такі способи представлення логічних функцій:

1. графічний;

2. табличний;

3. словесний:

4. аналітичний.

Прості логічні функції і, або, не. Логічні елементи

Логічну функцію (елемент) І школи називають функцією (елементом) типу «все або нічого».

На рис. 2.1 ілюструється принцип роботи елемента І з використанням механічних перемикачів (ключів).

Рисунок 2.1

В наведеній схемі логічні змінні А і В це стани від­повідних ключів. їх можна описати висловлюваннями "ключ замкнено"А=1, '' ключ розімкнено "-А=0. Ло­гічну функцію У описує висловлювання "горить чи не горить лампа", "горить" - У = 1. "не горить" - У =0.

Що потрібно зробити в схемі, щоб змусити лампу У на виході схеми загорітися? Потрібно замкнути ключ А і ключ В.

Функцію І інакше КОН'ЮНКЦІЯ, або ЛОГІЧНЕ МНОЖЕННЯ словесно можна описати так . "Функція істина якщо істині всі логічні змінні (і ар­гумент А і аргумент В).

У вигляді формули функцію можна записати

;

Табличним способом представлення логічної функції є таблиця істинно­сті.

Таблиця істинності функції І

А	В	Y
0	0	0
0	1	0
1	0	0
1	1	1

Таблиця істинності - матриця значень булевої функції, що відповідають всім можливим наборам двійкових аргументів ( для п логічних змінних кі­лькість N значень логічної функції: ).

Спосіб завдання логічної функції з допомогою таблиці істинності є на­глядним, але громіздким, особливо для великого числа аргументів. Таблиця істинності для функції чотирьох змінних має 16 рядків, а восьми - 256.

Логічний елемент (ЛЕ). Термін «логічний» в більшості застосовують по відношенню до процедури прийняття рішення. В такому випадку можна сказати, що логічний елемент - це схема, яка, згідно інформації вхідних си­гналів, «може вирішувати», що відповісти на виході - «ТАК» чи «НІ». Логі­чні елементи складаються з певної кількості діодів і транзисторів, і є елеме­нтами

Рисунок 2.2

інтегральної мікросхеми. Логічний елемент І, має прийняте умовне позначення, наведене на рис.2.2.

Такі позначення прийня­ті в країнах бувшого СРСР (за системою ГОСТ), в Англії і деяких інших країнах. В США прийняті позначенні ЛЕ за системою МIL/АNSI. Ці позначення подано в кінці розділу.

В комп'ютерній схемотехніці в більшості випадків за логічний нуль приймають низький рівень напруги (близько 0В) а за логічну одиницю високий рівень напруги (в залежності від типу логічних мікросхем наприклад на платах комп'ютерних схем це близько +5 В).

Для логічного елемента І на виході з'являється сигнал ВИСОКОГО логі­чного рівня тільки тоді, коли на всі його входи подаються, також, сигнали ВИСОКОГО рівня.

Найпростіший ЛЕ І можна утворити використовуючи діоди і опір, схема пристрою наведена на рис 2.3.

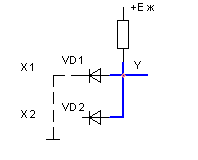
Рисунок 2.3

Робота схеми повинна відповідати таблиці істин­ності елемента І. Якщо на входи XI і Х2 подати сиг­нали напруги ВИСОКОГО рівня то діоди VD1 і VD2 будуть закриті і струм через резистор К проходити не буде. Напруга на виході дорівнює напрузі жив­лення. Таким чином на виході з'являється сигнал ВИСОКОГО рівня. У= "1".

Розглянемо випадок, коли на будь-який з входів (або на обидва) подати сигнал НИЗЬКОГО рівня, в найпростішому випадку це потенціал спільного проводу. Наприклад подамо низький рівень напруги на вхід XI. Діод VD1 в цьому випадку відкриваєть­ся і через нього проходить струм по колу +Еж→R→VD1->Х1→спільний провід.

Резистор і відкритий діод утворюють подільник напруги. Спад напруги на відкритому кремнієвому діоді приблизно 0,6В Потенціал на виході, від­носно спільного проводу буде дорівнювати спаду напруги на відкритому діоді. Це не нульова напруга, проте вона вважається сигналом НИЗЬКОГО логічного рівня. Таким чином на виході з'являється логічний 0. Робота схе­ми відповідає таблиці істинності елемента І.

Рисунок 2.4

Логічну функцію (елемент) АБО інколи називають елементом типу: '"будь-що або все".

Таблиця істинності

А	В	Y
0	0	0
0	1	1
1	0	1
1	1	1

На рис. 2.4 ілюструється прин­цип роботи елемента АБО з використанням звичайних перемикачів.

Очевидно, що лампа на виході схеми буде горіти,

якщо будь-який з ключів або обидва відразу вияв­ляться замішу тими і, навпаки, не буде горіти, якщо обидва ключа розімкнуті.

Функцію АБО інакше ДИЗ'ЮНКЦІЯ, або ЛОГІЧНЕ ДОДАВАННЯ можна описати так. "Функ­ція істина якщо істині перша АБО друга, АБО третя, АБО всі логічні змінні (АБО А, АБО В, АБО А і В).

Аналітичний спосіб представлення (формула):

На рис. 2.5 представлено позначення ЛЕ АБО.

Рисунок 2.5

Найпростіший ЛЕ АБО, на діодах і резисторі має схему рис. 2.6.

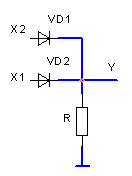
Рисунок 2.6

Розглянемо роботу схеми. Перший випадок коли на будь-який з входів (або на обидва) подати сигнал ВИСОКОГО логічного рівня, в найпростішому випадку це потенціал живлення. Наприклад подамо високий рі­вень напруги на вхід XI. Діод VD1 в цьому випадку від­кривається і через нього буде проходити струм по колу спільний провід. Резистор і відкритий діод утворюють подільник на­пруги. Потенціал на виході, відносно спільного проводу буде на 0,6В менше напруги живлення. Ця напруга вва­жається сигналом ВИСОКОГО логічного рівня. Таким чином на виході з'являється логічна 1.

Низький логічний рівень, тобто Y = 0 буде в тому випадку якщо на обидва входи XI і Х2 подані низькі рівні напруги.

Робота схеми відповідає таблиці істинності елемента АБО.

Логічна функція (елемент) НЕ.

Рисунок 2.7

Всі логічні елементи, розглянуті вище, мали принаймні два входи і один вихід. На відміну від них в схемі НЕ, що називається інвертором, є тільки один вхід і один вихід. Основна функція схеми НЕ в тому, щоб забезпечувати на виході сигнал, протилежний сигналу на вході.

Лампа на виході схеми не буде горіти Y=0, якщо ключ натиснути і, навпаки, буде горіти, якщо ключ А відпустити (тобто замкнути).

Функцію НЕ, інакше ІНВЕРСІЯ, або ЛОПЧНЕ ЗАПЕРЕЧЕННЯ можна описати так. "Функція істина якщо вхідна логічна змінна помилкова"

Якщо подати логічний сигнал "1" (високий рівень) на вхід схеми, то на виході У буде сигнал низького рівня, тобто логічний "0". Кажуть, що ЛЕ НЕ інвертує вхідний сигнал.

Таблиця істинності

A	Y
0	1
1	0

Булевий вираз для логічної функції НЕ

Y = Ā "Y дорівнює не А".

На рис.2.8 показано умовне позначення інвертора.

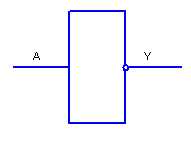
Рисунок 2.8

Електронний пристрій, що виконує роль елемента НЕ це електронний ключ. Робота електронних ключів розглянута в додатко­вих темах.

Складні логічні функції і логічні елементи

Загальна кількість логічних функцій F

від п двійкових змінних

Для одного аргументу існує 4 двійкові функції (табл. 2.1):

Таблиця 2.1

X	Y0	Y1	Y2	Y3
0	0	0	1	1
1	0	1	0	1

Y0 = 0 - константа 0,

YЗ = 1 - константа 1,

Y1 = X - повторення X.

Y2 відома нам функція НЕ (інверсія X):

Функції одного аргументу називають унарними.

Кількість двійкових функцій двох змінних дорівнює 16 , з .яких шість - вироджені: YО = 0 - константа 0, Y15 = 1 - константа 1, YЗ - змінна А, Y5 - змінна В, Y10 - інверсія В, Y12 - інверсія А

Фактично табл.2.1 є сукупністю чотирьох, а табл.2.2 - шістнадцяти таблиць іс­тинності.

Таблиця 2.2

A	B	Y0	Y1	Y2	Y3	Y4	Y5	Y6	Y7	Y8	Y9	Y10	Y11	Y12	Y13	Y14	Y15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	1	0	0	0	1	1	1	0	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Не всі логічні функції реалізовані у вигляді мікросхем і мають потребу з техні­чної точки зору. Розглянемо декілька основних логічних функцій, що мають засто­сування в комп'ютерній схемотехніці.

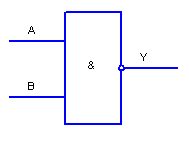
Рисунок 2.9

Функція 1-НЕ (В таблиці 2.2 - стовпчик Y14)

Стовпчик Y14 для елемента І-НЕ одержують інвер­туванням виходу елемента І. функція якого наведена в тій самій таблиці в стовпчику YI .

Логічні елементи 1-НЕ дуже поширені в схемах про­мислової електроніки, а також в цифрових електронних приладах всіх типів.

Функція логічного елемента І-НЕ в тому, що на його виході з'являється сигнал ВИСОКОГО рівня тоді, коли на один з його входів подано сигнал НИЗЬКОГО рівня.

Позначення ЛЕ І-НЕ наведено на рис. 2.8.

Функція АБО-НЕ (Y8)

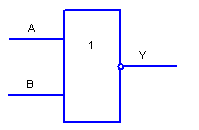
Рисунок 2.10

Стовпчик Y8 для елемента АБО-НЕ одержують шля­хом інвертування виходу елемента АБО. функція якого наведена в тій самій таблиці в стовпчику Y7.

Відокремлювана властивість логічного елемента АБО-НЕ в тому, що на його виході з'являється сигнал ВИСОКОГО рівня тільки тоді, коли на всі його входи подаються сигнали НИЗЬКОГО рівня. А в усіх інших випадках на виході формується сигнал логічного нуля.

Логічна функція "Виключне АБО" ("Нерівнозначність") (Y6)

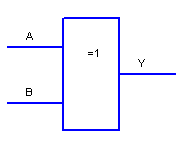
Рисунок 2.11

Словесно описати роботу функції "Нерівнозначність" можна так: "У - істина (дорівнює 1) якщо вхідні сигнали не рівні між собою", часто для цієї функції використо­вують скорочення ХОR. Булевий вираз для "Виключне АБО"

Логічна функція виключне АБО-НЕ ("Рівнозначність")( У9)

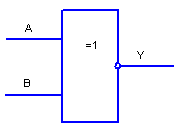
Рисунок 2.12

Словесно описати роботу функції "Рівнозначність" можна так "Y - істина (дорівнює 1) якщо вхідні сигнали рівні між собою", часто для нього використовують ско­рочення XNOR.

Булевий вираз для "виключне АБО-НЕ"

Логічна функція "Заборона" (Y2)

Рисунок 2.13

Словесно описати функцію логіч­ного елементу "Заборона"' можна так: "Елемент має два входи.

Інформацій­ний вхід А і вхід заборони В. Вихід Y - повторює сигнал на інформаційно­му вході А, якщо В - В той момент коли подано сигнал заборони В = 1. то на виході У = 0. незалежно від сигналів на вході В"

Функція "Заборона" утворюється шляхом інвертування одного з входів

елементу І (рис2.12.6). Булевий вираз для функції " "Заборона" - Y = А • В

Позначення ЛЕ прийняті в американському стандарті МІL/АNSI наведені на рис 2.14.

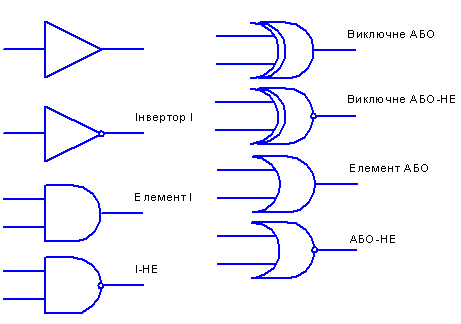
Рисунок 2.14-позначення логічних елементів в системі MIL/ANSI

Буфер. Буфер не змінює логічного стану цифрового сигналу, тобто "1" (чи "0") на вході викликає "1" (чи "0") на виході. Буфери застосовуються для під­вищення навантажувальної здатності по струму.

ЗАКОНИ АЛГЕБРИ ЛОГІКИ, ЛОГІЧНИЙ СИНТЕЗ

В більшості випадків при конструюванні цифрових електронних схем розробнику приходиться мати справу з завданням, яке надається йому сло­весно, або у вигляді таблиці, організованої таким чином, що комбінації вхідних сигналів відповідає потрібний вихідний.

Рисунок 3.1

Для створення схеми, яка буде виконувати логічні функції, і забезпечувати роботу при­строїв автоматики, схеми керування, необхідно чітко уявляти собі закони які регламентують створення логічних схем. Створення логічних схем згідно заданого словесно завдання називається логічним синтезом.

Пристрій що виконує задані булеві функції називається цифровим ав­томатом.

Порядок логічного синтезу такий:

Із словесно заданого виразу потрібно скласти таблицю істинності, тобто впорядкувати в таблицю задані дії пристрою. За існуючим алгоритмом скласти булеве рівняння в одній з нормальних форм. Таких форм дві: Диз’юконтивна нормальна форма (ДНФ), тобто сума добутків логічних ар­гументів і кой кон'юнктивна нормальна форма (КНФ), добуток сум логічних аргументів. Як правило отриманий вираз має надлишкові операції, тому йо­го необхідно спростити, тобто створити досконалу форму (наприклад До­сконалу ДНФ, ДДНФ) 3 логічного виразу складають схему на простих логі­чних елементах або переходять на заданий базис логічних мікросхем.

Порядок синтезу можна скорочено представити такою схемою:

1. Із словесно заданого виразу —> Таблицю істинності;

2. З таблиці істинності —> Булевий вираз ДНФ або КНФ;

3. Спрощення булевого виразу з ДНФ—>ДДНФ;

4. Складання схеми на простих ЛЕ;

5. Переведення в базис І-НЕ (АБО-НЕ) Складання

схеми.

Алгоритм складання ДНФ:

1. скласти кон'юнкції (добутки) логічних змінних для рядків таблиці іс­тинності, де логічна функція дорівнює І, логічна змінна входить до кон'юн­кції інвертованою, якщо її значення в даному рядку дорівнює 0,

2. об'єднати диз'юнкцією всі одержані кон'юнкції (суму добутків).

Алгоритм складання КНФ:

1. сктасти диз'юнкції логічних змінних для рядків таблиці істинності, де логічна функція дорівнює 0, логічна змінна входить до кон'юнкції інверто­ваною, якщо її значення в даному рядку дорівнює 1,

2. скласти кон'юнкцію одержаних диз'юнкцій (добуток сум).

Теорія булевих функцій

Булевими функціями називають функції, які так само, як і їх аргументи, приймають тільки два значення: Oil. Булеві функції можуть бути задані у вигляді формул або таблиць. Цс можуть бути як стандартні логічні функції (ЛФ), які були розглянуті вище, так і розроблені схеми на базі відомих фун­кцій.

Для складання логічного синтезу важливо знати основні закони,теореми алгебри логіки.

Теореми алгебри логіки

Одним з ефективних методів доказ)' теорем є метод перебору всіх зна­чень змінних: якщо теорема істинна, то при підстановці будь-яких значень змінних в обидві частини виразу, що формулює теорему, повинно вийти тотожність.

1) закони тавтології

;

2) комутативні закони

;

3. асоціативні закони

;

4. дистрибутивні закони

;

5. закони заперечення

; ;

6) закони подвійності (де Моргана)

;

7) закони нульових і одиничних аргументів

; ;

;

8) закон поглинання

;

9) закон склеювання

;

;

Методи мінімізації булевих функцій

Суть методу безпосередніх перетворень полягає в том)/, що мінімізація початкової логічної функції проводиться шляхом застосування до окремих членів або груп членів формули, що виражає дану логічну функцію, основ­них законів алгебри логіки з мстою отримання мінімальної форми функції, тобто такий, який не містить зайвих змінних або членів.

Зайвими змінними або членами є ті, які не впливають на значення фор­мули, що перетворюється. Наприклад для спрощення рівняння можна за­стосувати склеювання:

тобто в початковій формулі зайвою була двійкова змінна XI.

Дії, що відповідають методу безпосередніх перетворень, звичайно про­водяться в наступному" порядку:

Виявляються групи двійкових змінних початкової формули, до яких мо­жна застосувати операцію склеювання або інші закони алгебри логіки, що приводять вирази до більш простої форми.

Порядок склеювання:

- виконують склеювання першого добутку з всіма решта з якими можливо;

- виконують склеювання другого добутку з всіма крім першого;

- виконують склеювання третього добутку з всіма крім першого і друго­го і т.д.

Якщо після першого склеювання з'являються групи які також можна склеювати, операції повторюють в тому ж порядку.

Недоліком методу безпосередньої мінімізації є складність отримання всіх мінімальних форм, якщо їх декілька. Крім того, метод загалом вельми трудомісткий, результат мінімізації в значній мірі залежить від кваліфікації і інтуїції людини, що проводить мінімізацію. Тому даний метод застосову­ється лише для мінімізації простих логічних формул.

.

• дві сусідніх клітинки;

• два протилежних кінця одного рядка;

• два протилежних кінця одного стовпця.

При угрупуванні одиниць на діаграмі необхідно спробувати спочатку утворити члени, що містять одну змінну, потім члени, що містять дві змінні, і, нарешті, члени, що містять три змінні.

При складанні добутків аргументів необхідно визначите такі аргументи які в кожному контурі повторюються без змін в усіх клітинках.

ТРИГЕРИ . ПРИНЦИПИ ОРГАНІЗАЦІЇ ТРИГЕРНИХ СХЕМ

Практично всі пристрої цифрової техніки суміщають функції переробки і зберігання інформації. Невід'ємна частина таких пристроїв - елемент па­м'яті. Для зберігання інформації найчастіше використовують елемент з дво­ма стійкими станами тригер.

Назва тригер походить від англійського trigger - спусковий гачок. Вже з назви можна скласти деяку уяву про роботу тригерних схем по аналогії з вогнепальною зброєю. Стрілець порівняно тривалий час. повільно, стараю­чись не збити приціл натискає на гачок доки той не доходить до точки пост­рілу тоді пружина зривається і бойок з великою швидкістю вдаряє по кап­сулю тобто стан змінюється дуже швидко.

У загальному вигляді будь-який тригер можна розглядати як пристрій, що має кілька керуючих входів і два виходи. Виходи тригера позначають

символами Q і Q; їх називають відповідно прямим та інверсним. Умовне графічне позначення тригера подано на рис. 4.1.

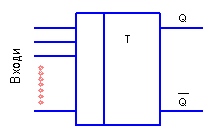
Рисунок 4.1

Якщо на прямому виході тригера внаслідок певних вхідних впливів ви­никає напруга, що відповідає значенню логічної " 1", то кажуть, що тригер перейшов в одиничний стан. Нага­даємо, що під логічною "1" розуміють наявність високо­го рівня напруги точно визначеного значення.

Якщо на прямому виході тригера під дією вхідних електричних сигналів напруга набуде значення, що дорівнює логічному "0", тобто значення, близького до нуля, то кажуть, що тригер перебуває в нульовому стані.

Таким чином, тригер - електронний пристрій, який може перебувати в одному" з двох стійких станів - одиничному або нульовому. Перехід з одно­го стану в інший здійснюється під час подання певних значень електричних сигналів на відповідні входи. Якщо таких сигналів не буде, то тригер збері­гає свій останній стан.

З точки зору інформатики Тригер - логічний, послідовніший пристрій, здатний зберігати і біт інформації.

Напруга на інверсному виході завжди має значення, обернене логічному стану прямого виходу, тобто якщо 0=1 то 0 = 1.

На відповідні входи тригерів подають інформаційні і керуючі сигнали.

Інформаційними називають сигнали що несуть інформацію, яку тригеру треба запам'ятати.

Керуючі-це ті сигнали, після подання яких інформація записується в тригер.

За способом запису інформації розрізняють асинхронні і синхронні триге­ри. У асинхронних тригерах перехід у новий стан спричинюється змінами ін­формаційних вхідних сигналів. У синхронних тригерах такий перехід відбува­ється тільки після подання спеціальних сигналів, які називають тактовими або синхронізуючими, вхід тригера, на який надходять такі сигнали, назива­ють тактовим і позначають літерою С. (від англійського clock - такт).

За способом сприйняття тактових сигналів розрізняють тригери, які ке­руються рівнями і перепадами напруг. Керування рівнями означає, що при одному рівні напруги на тактовому вході тригер перебуває в певному режи­мі (наприклад, зберігає раніше записану інформацію), а при другому - він переходить в інший режим (наприклад, змінює свій стан). Якщо тригер ке­рується перепадами напруги, то такий дозвіл га запам'ятовування вхідної інформації тригером дається в момент перепаду тактового сигналу з одного рівня на другий. В інші моменти тригер не сприймає вхідні інформаційні сигнали. Тригери такого типу називають тригерами з динамічним керуван­ням.

Закони функціонування тригерів задаються таблицями переходів або складеними відповідно до цих таблиць логічними рівняннями.

Входи тригерів позначаються таким чином: С вхід синхронізації ;

J вхід установки JK-тригера в 1;

S (set) вхід установки тригера в 1;

К вхід установки JK-тригера в 0; R (reset) вхід скидання тригера в 0 ;

V керуючий вхід DV-тригера; D (delay) «затримка» ;

Т (trigger) «клямка» ;

Виходи тригерів: Q - прямий вихід Q- інверсний вихід

Защіпка

В основі запам'ятовуючої комірки будь-якого тригера лежить защіпка, рис. 4.2.а.

Рисунок 4.2.a

Защіпка являє собою кільце складене з двох інверторів, вихід кож­ного з них визначає стан наступного, тому зразу після подання живлення схема встановиться в довільний, рів­но ймовірний стійкий стан, в якому буде знаходитись до відключення живлення.

Чому такий стан буде стійким? Якщо на виході ЛЕ DDI утворюється більш високий рівень напруги - це веде до того що на виході DD2 утвориться більш низь­кий рівень, а значіть більш низький рівень на вході ін­вертора DD2, що ще збільшує рівень на його виході.

Таким чином утворюється замкнуте коло позитивного Рисунок 4.2 зворотного зв'язку, що забезпечує стійкий стан схеми. Защіпку прийнято креслити так як показано на рис. 4.2.б.

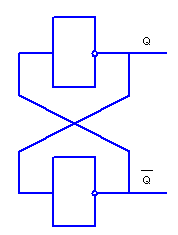
Рисунок 4.2.б

Але защіпка, хоч і має вже вигляд притаманний тригеру, має виходи Q і Q, але вона ще не тригер, оскільки в ній немає входів, з допомогою яких можна в процесі роботи змінювати стан схеми.

Для того щоб створити тригер необхідно інвертори в защіпці замінити на елементи І-НЕ чи АБО-НЕ. Той тригер який буде утворюватись називають асинхронним RS тригером.