
Розрахункова робота № 3 Діагностування стану двигуна за наявності одного діагностичного параметра за допомогою методу мінімального ризику
Мета роботи
Мета роботи - ознайомитися із статистичним методом мінімальної ризику для діагностування технічного стану двигуна, побудувати криві нормального розподілу і визначити граничне значення діагностичного параметра X0.
Короткі теоретичні відомості
Руйнування деталей двигуна у багатьох випадках починається з відфарбовування поверхневого шару під впливом динамічних навантажень і сил тертя. Продукти зносу деталей, що утворюються при цьому, несуться циркулюючим в двигуні мастилом, тому воно є носіїв інформації про процеси, що відбуваються при зношуванні. Кількість продуктів зносу, що поступають в мастило, залежить, перш за все, від швидкості зносу, тому інтенсивність накопичення цих продуктів в маслі є вельми коштовною діагностичною ознакою технічного стану (ТС) деталей, приводів і так далі.
Для контролю ТС і діагностування двигуна в даний час поширення набувають такі фізичні методи, як диференціально-магнітний метод (ДМ - метод) діагностування, метод спектрального аналізу мастила та ін. . Вони засновані на аналізі продуктів зносу деталей омиваних мастилом. Ці методи мають як позитивні аспекти, так і недоліки. До недоліків слід віднести відсутність методики ухвалення рішення за швидкістю підвищення концентрації металів і їх кількості.
Окрім фізичних методів діагностування стану двигуна за допомогою технічних засобів, в даний час усе більш широкого визнання і популярності набувають методи статистичних рішень.
Методи статистичних рішень успішно використовуються в завданнях технічної діагностики виробів машинобудування і відрізняються від фізичних методів правилами ухвалення рішення. В даний час для оцінки технічного стану двигуна можуть застосовуватися наступні методи статистичних рішень:
- метод мінімального ризику;
- метод мінімального числа помилок;
- метод мінімакса;
- метод Неймана - Пірсону;
- метод найбільшої правдоподібності.
Процес розпізнавання технічного стану двигуна за допомогою методів статистичних рішень можна проводити за наявності одного діагностичного параметра, за наявності зони невизначеності, за наявності двох або декількох станів, а також при багатовимірних розподілах діагностичних параметрів.
Процес розпізнавання технічного стану розглянемо на прикладі наявності одного діагностичного параметра двигуна, тобто вміст металу в маслі. Маємо два розподіли випадкових значень діагностичного параметра, властивих справним і несправним однотипним двигунам, приведених на рисунку 3.
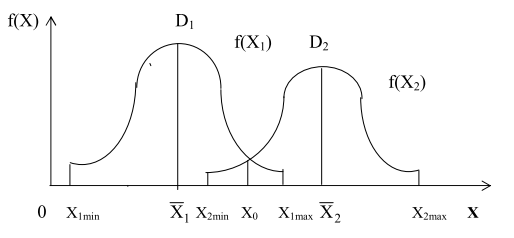
Рис. 3. Статистична щільність розподілу вірогідності параметра X для справного D1 і несправного D2 перебувань
На рис. 3: X - значення діагностичного параметра ( X1 - середнє значення діагностичного параметра для справного стану; X2 - середнє значення діагностичного параметра для несправного стану); Х1min і Х2min мінімальні значення діагностичного параметра для справного і несправного станів; Х1max і X2max – максимальні значення діагностичного параметра справного і несправного станів; X0 - граничне значення діагностичного параметра.
Статистичні рішення за допомогою перерахованих методів як для одного діагностичного параметра, так і для декількох завжди починається з вибору правила ухвалення рішень, тобто в зоні пересічення розподілів треба вибрати значення X0 параметра X таким чином, що при X > X0 слід прийняти вирішення про подальшу експлуатацію двигуна, а при X < X0 він допускається до подальшої експлуатації.
Тоді вказане правило ухвалення рішення полягає в наступному:
при X < Х0 X € D1 при X > Х0 X € D2. ( 1 )
Прикладом - такого роду завдань можуть служити: визначення граничного значення вмісту металу в маслі двигуна, граничного рівня його вібрацій, величини люфта сполучення, що відповідає граничному зносу зв'язаних елементів і так далі.
Із залежностей, які представлені на рис. 3, видно, що області справного D1 і несправного D2 станів перетинаються, отже, в принципі неможливо вибрати значення X0, при якому прийняте правило рішення (1) не давало б помилкових результатів. Рішення надалі повинне зводитися до того, щоб вибір Х0 був в деякій сенсі оптимальним, тобто давав найменше число помилкових рішень. При ухваленні рішень можливими помилками можуть бути: «помилкова тривога» (помилка першого роду) - коли справний об'єкт вважається несправним і «пропуск дефекту» (помилка другого роду) - коли несправний об'єкт визнається справним. У теорії контролю прийняті позначення: С21 – помилкова тривога; С12 – пропуск дефекту (перша цифра нижнього індексу відповідає індексу прийнятого діагнозу, друга цифра - індексу дійсного стану).
Найбільш прийнятним з вищезгаданих методів статичних (аналітичних) рішень для визначення граничного значення діагностичного параметра Х0 є метод мінімального ризику.
Значення Х0 в цьому методі знаходиться із співвідношення:
 ,
(2)
,
(2)
де F(X1/ D1) - щільність нормального розподілу вірогідності для справного стану; F(X2/D2) - щільність нормального розподілу вірогідностей для несправного стану; C12 - умовна вартість пропуску дефекту; С21-умовна вартість помилкової тривоги; Р1 - апріорна вірогідність справного стану; P2 - апріорна вірогідність несправного стану; C11 < 0, C22 < 0 - ціни правильних рішень (умовні вірогідності).
Щоб побудувати функціональну залежність F(X1/ D1), необхідно зібрати і обробити статистичні дані, які відображали б окремі значення діагностичних параметрів для справних об'єктів. Практика показує, що об'єм даних має бути не менше 40 значень. Аналогічно будується і F(X2/D2). Функції щільності розподілу вірогідності для Х1 і Х2 в даному випадку виглядатимуть так:
 (3)
(3)

де s - середньоквадратичне відхилення для кожного з розподілів; е - підстава натурального логарифма (2, 72); X - поточне значення діагностичного параметра; X1 і X2 - середнє значення діагностичного параметра.
Оперуючи умовними вартостями помилок, слід мати на увазі, що для відмов, що безпосередньо впливали на працездатність двигуна С12/С21 = 20 - 35, а для «безпечних» відмов С12/С21=1. У завданнях технічної діагностики значення Р1 і Р2 в більшості випадків відомі за статистичними даними. Необхідно пам'ятати, що
P1+ P2 = 1,0.
Підставив (3) в співвідношення (2) та вирішивши рівняння, знайдемо Х0:
 (4)
(4)
Порядок виконання роботи
1. Ознайомитися із загальним положенням діагностування стану двигуна за допомогою методів статистичних рішень.
2. Вивчити методичні вказівки по виконанню практичної роботи.
3. Розрахувати параметри.
4. Побудувати функціональні залежності щільності розподілу вірогідності діагностичного параметра X для справного D1 і нєсправного D2 стану.
5. Визначити граничне значення діагностичного параметра X0, що забезпечує мінімум середнього ризику.
Методичні вказівки
Як об'єкт дослідження в даній практичній роботі розглядається двигун, у якого визначається вміст продуктів зносу (металу) в працюючому мастилі.
Працездатний стан двигуна в основному визначається станом деталей циліндропоршневої групи, кривошипно-шатуновий механізму, газорозподільного механізму і інших деталей, схильних до зношування, метал яких потрапляє в мастило.
Діагностування технічного стану двигуна визначається поодинці діагностичному параметру Х - вміст металу в мастилі.
Для побудови кривих нормального розподілу використовуються формули (3), для яких заздалегідь розраховуються параметри:
1) Xi - вміст металу в грамах на 1 тону мастила для i-го діагнозу, значення беруться з таблиці Додаток 2 відповідно варіанту;
2) Δ Xi - область (інтервал) вміст металу в мастилі визначається за формулою:
![]() (5)
(5)
де k - кількість інтервалів дроблення емпіричного ряду розподілу, зазвичай задається в межах 5...8. Для розрахунків в даній роботі беремо k=5;
3) X j,ср – средне значення вмісту (г) металу в мастилі в j–ом інтервалі:
![]() (6)
(6)
4)
![]()
 -
математичне
очікування
випадковой
величини
для
першої
чи
другої
кривої
розподілу
-
математичне
очікування
випадковой
величини
для
першої
чи
другої
кривої
розподілу
![]() (7)
(7)
де - m j – число випробувань, при якому Хi появилось в j-ом інтервалі; n – загальне число випробувань
 (
8
)
(
8
)
5) σі – середньоквадратичне відхилення випадкової величини
 (
9)
(
9)
6) t – нормоване відхилення
 (
10
)
(
10
)
( 10 )
Тоді
 (
11
)
(
11
)
Величина
![]() табульована і находиться з таблиці
Додатку 3.
табульована і находиться з таблиці
Додатку 3.
Зміст звіту
Звіт по практичній роботі повинен містити:
1. Мета роботи;
2. Короткі теоретичні відомості;
3. Розрахунок параметрів емпіричного розподілу металу в мастилі двигуна за початковими даними, приведеними в таблиці Додатку 2
4. Графік статичного розподілу щільності вірогідності діагностичного параметра Х для справного D1 і несправного D2 станів двигуна.
5. Розрахунок граничного значення діагностичного параметра Х0.
6. Висновки.
Розрахункова робота № 4
Діагностування двигуна по одному параметру за допомогою методу
Неймана - Пірсону
Мета роботи
Мета роботи - ознайомитися з методом Неймана - Пірсону і застосування його для діагностування двигуна, визначити величину Х0 і значення середнього ризику.
Короткі теоретичні відомості
Вказаний метод є одним з методів статистичних рішень. Він застосовується тоді, коли оцінки вартості помилок невідомі і їх достоверне визначення пов'язане з великими труднощами. Проте у всіх випадках бажано при певному (допустимому) рівні однієї з помилок мінімізувати значення іншої. Завдання в цьому випадку полягає в обгрунтованому вибору допустимого рівня помилок за допомогою попереднього досвіду або інтуїтивних міркувань.
По даному методу мінімізується вірогідність пропуску дефекту при заданому допустимому рівні вірогідності помилкової тривоги. Звідси, вірогідність помилкової тривоги
 (
1 )
(
1 )
де А - заданий допустимий рівень вірогідності помилкової тривоги; Р1 - вірогідність справного стану; Р2 - вірогідність несправного стану.
Зазвичай умову (1) відносять до умовної вірогідності помилкової тривоги
коли множник Р1 відсутній. У завданнях технічної діагностики значенія Р1 і Р2 в більшості випадків відомі за статистичними даними.
З рис. 3 видно, що збільшення вірогідності помилкової тривоги (значення Х0 переміщається вліво) величина вірогідності пропуску дефекту зменьшаєтся. Її найменше значення відповідатиме знаку рівності в умові (1):
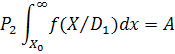 (
2 )
(
2 )
Тоді умова (1) однозначно визначає величину Х0 і значення середнього ризику.
У практичних завданнях приймають значення А - допустимого рівня помилкової тривоги.
A = kP2 ( 3 )
де k - коефіцієнт надмірності, залежний від роздільної здатності діагностичних засобів, небезпеки дефекту, економічних витрат і інших обставин.
При дефектах з обмеженими наслідками можна приймати k=1...3. При небезпечних дефектах k=3...10. Для дефектів, що рідко зустрічаються (Р2<0,01), для вкрай небезпечних, коефіцієнт надмірності може досягати і великих значень.
У завданнях технічної
діагностики
можна
використовувати
і інший
підхід:
визначати граничне
значення
X0,
виходячи з вибраної
вірогідності пропуску
дефекту.
В цьому випадку
завданнях технічної
діагностики
можна
використовувати
і інший
підхід:
визначати граничне
значення
X0,
виходячи з вибраної
вірогідності пропуску
дефекту.
В цьому випадку
( 4 )
де В - задане значення вірогідності пропуску дефекту.
Величина В повинна вибиратися з урахуванням вказаних вище міркувань. Якщо дефект вкрай небажаний навіть для одиничного виробу, то можна приймати
![]()
( 5 )
де N - загальне число двигунів, що знаходяться в експлуатації; k - коефіциєнт надмірності (1<=k<10). У всіх випадках, для реалізації прінципу неможливості маловірогідних подій, величина В повинна бути малою (В<0,01). У методі Неймана - Пірсона граничне значення X0 знаходиться з рівняння (2) або (4).
При практичному вирішенні подібних рівнянь доцільно використовувати метод Ньютона, що зв'язує початкові X0(n-1) і подальші X0(n) наближення
 (
6 )
(
6 )
Вважаючи, що
 (
7 )
(
7 )
 (8)
(8)
Як перше наближення можна прийняти
![]() (
9
)
(
9
)
Де X1, X2 - середні значення Х для розподілу f(X/D1) і f(X/D2).
При послідовному ітераційному обчисленні значення Х0, ми прагнемо до такого стану, при якому мінімізується середній ризик. При достатній близькості X0(n) і X0(n-1) приймається Х0 = Х0(n).
Середній ризик ґрунтується на вірогідності ухвалення помилкового рішення доданку з вірогідності помилкової тривоги і пропуску дефекту, а також вартості цих помилок. У загальному випадку середній ризик (очікувана величина втрати) виражається рівністю

(10)
де С11, С22 - вартості правильних рішень, які в порівнянні з вартостями помилкових рішень приймаються негативними.
Величина Х, що пред'являється для розпізнавання, є випадковою і тому за рівнянням (10) є математичним очікуванням ризику.
Порядок виконання роботи
1. Вивчити методичні вказівки по виконанню практичної роботи.
2. Визначити вірогідність помилкової тривоги.
3. Визначити вірогідність пропуску дефекту.
4. Методом Ньютона визначити значення Х0.
5. Обчислити значення середньої риски.
6. Провести аналіз отриманих результатів.
7. Оформити звіт.
додаток 1
Таблиця варіантів завдань для виконання практической роботи № 1
Номер завдання |
Стан |
Вірогідністі проявлення ознак |
||||
P(K 1/D i) |
P( К 1/D i) |
P(K 2/Di) |
P( К 2/D i) |
P(D i) |
||
1 |
D1 |
0,2 |
0,8 |
0,8 |
0,2 |
0,7 |
D2 |
0,6 |
0,4 |
0,3 |
0,7 |
0,2 |
|
D3 |
0,8 |
0,2 |
0,2 |
0,8 |
0,1 |
|
2 |
D1 |
0,3 |
0,7 |
0,6 |
0,4 |
0,1 |
D2 |
0,7 |
0,3 |
0,1 |
0,9 |
0,2 |
|
D3 |
0,9 |
0,1 |
0,3 |
0,7 |
0,7 |
|
3 |
D1 |
0,4 |
0,6 |
0,5 |
0,5 |
0,2 |
D2 |
0,8 |
0,2 |
0,3 |
0,7 |
0,1 |
|
D3 |
0,7 |
0,3 |
0,4 |
0,6 |
0,7 |
|
4 |
D1 |
0,5 |
0,5 |
0,7 |
0,3 |
0,2 |
D2 |
0,6 |
0,4 |
0,1 |
0,9 |
0,2 |
|
D3 |
0,1 |
0,9 |
0,7 |
0,3 |
0,6 |
|
5 |
D1 |
0,1 |
0,9 |
0,8 |
0,2 |
0,5 |
D2 |
0,2 |
0,8 |
0,3 |
0,7 |
0,2 |
|
D3 |
0,3 |
0,7 |
0,2 |
0,8 |
0,3 |
|
6 |
D1 |
0,2 |
0,8 |
0,4 |
0,6 |
0,1 |
D2 |
0,3 |
0,7 |
0,3 |
0,7 |
0,2 |
|
D3 |
0,4 |
0,6 |
0,2 |
0,8 |
0,7 |
|
7 |
D1 |
0,3 |
0,7 |
0,5 |
0,5 |
0,6 |
D2 |
0,4 |
0,6 |
0,4 |
0,6 |
0,3 |
|
D3 |
0,5 |
0,5 |
0,3 |
0,7 |
0,1 |
|
8 |
D1 |
0,4 |
0,6 |
0,6 |
0,4 |
0,1 |
D2 |
0,5 |
0,5 |
0,4 |
0,6 |
0,2 |
|
D3 |
0,6 |
0,4 |
0,5 |
0,5 |
0,7 |
|
9 |
D1 |
0,5 |
0,5 |
0,7 |
0,3 |
0,7 |
D2 |
0,6 |
0,4 |
0,6 |
0,4 |
0,1 |
|
D3 |
0,7 |
0,3 |
0,5 |
0,5 |
0,2 |
|
10 |
D1 |
0,6 |
0,4 |
0,8 |
0,2 |
0,4 |
D2 |
0,7 |
0,3 |
0,7 |
0,3 |
0,4 |
|
D3 |
0,8 |
0,2 |
0,6 |
0,4 |
0,2 |
|
11 |
D1 |
0,7 |
0,3 |
0,9 |
0,1 |
0,8 |
D2 |
0,8 |
0,2 |
0,8 |
0,2 |
0,1 |
|
D3 |
0,9 |
0,1 |
0,7 |
0,3 |
0,1 |
|
12 |
D1 |
0,8 |
0,2 |
0,1 |
0,9 |
0,6 |
D2 |
0,9 |
0,1 |
0,9 |
0,1 |
0,3 |
|
D3 |
0,1 |
0,9 |
0,8 |
0,2 |
0,1 |
|
13 |
D1 |
0,9 |
0,1 |
0,4 |
0,6 |
0,4 |
D2 |
0,7 |
0,3 |
0,9 |
0,1 |
0,3 |
|
D3 |
0,4 |
0,6 |
0,2 |
0,8 |
0,3 |
|
14 |
D1 |
0,1 |
0,9 |
0,8 |
0,2 |
0,5 |
D2 |
0,4 |
0,6 |
0,3 |
0,7 |
0,2 |
|
D3 |
0,8 |
0,2 |
0,7 |
0,3 |
0,3 |
|
21
 додаток
2
додаток
2
Таблиця вихідних даних для практических робіт № 2, № 3 и № 4
№ Варіант 1 Варіант 2 Варіант 3 Варіант 4
п/п D1 D2 D3 D1 D2 D3 D1 D2 D3 D1 D2 D3
1. 2,0 5,0 8,0 3,0 6,0 9,0 4,0 7,0 10,0 5,0 8,0 11,0
2. 2,9 5,9 8,9 3,9 6,9 9,9 4,9 7,9 10,9 5,9 8,9 11,9
3. 1,6 4,6 7,6 2,6 5,6 8,6 3,6 6,6 9,6 4,6 7,6 10,6
4. 1,3 4,3 7,3 2,3 5,3 8,3 3,3 6,3 9,3 4,3 7,3 10,3
5. 1,6 4,6 7,6 2,6 5,6 8,6 3,6 6,6 9,6 4,6 7,6 10,6
6. 2,4 5,4 8,4 3,4 6,4 9,4 4,4 7,4 10,4 5,4 8,4 11,4
7. 2,9 5,9 8,9 3,9 6,9 9,9 4,9 7,9 10,9 5,9 8,9 11,9
8. 1,6 4,6 7,6 2,6 5,6 8,6 3,6 6,6 9,6 4,6 7,6 10,6
9. 0,3 3,3 6,3 1,3 4,3 7,3 2,3 5,3 8,3 3,3 6,3 9,3
10. 2,5 5,5 8,5 3,5 6,5 9,5 4,5 7,5 10,5 5,5 8,5 11,5
11. 1,6 4,6 7,6 2,6 5,6 8,6 3,6 6,6 9,6 4,6 7,6 10,6
12. 2,3 5,3 8,3 3,3 6,3 9,3 4,3 7,3 10,3 5,3 8,3 11,3
13. 2,0 5,0 8,0 3,0 6,0 9,0 4,0 7,0 10,0 5,0 8,0 11,0
14. 2,0 5,0 8,0 3,0 6,0 9,0 4,0 7,0 10,0 5,0 8,0 11,0
15. 0,5 3,5 6,5 1,5 4,5 7,5 2,5 5,5 8,5 3,5 6,5 9,5
16. 2,5 5,5 8,5 3,5 6,5 9,5 4,5 7,5 10,5 5,5 8,5 11,5
17. 2,9 5,9 8,9 3,9 6,9 9,9 4,9 7,9 10,9 5,9 8,9 11,9
18. 2,4 5,4 8,4 3,4 6,4 9,4 4,4 7,4 10,4 5,4 8,4 11,4
19. 2,1 5,1 8,1 3,1 6,1 9,1 4,1 7,1 10,1 5,1 8,1 11,1
20. 1,1 4,1 7,1 2,1 5,1 8,1 3,1 6,1 9,1 4,1 7,1 10,1
21. 0,9 3,9 6,9 1,9 4,9 7,9 2,9 5,9 8,9 3,9 6,9 9,9
22. 2,9 5,9 8,9 3,9 6,9 9,9 4,9 7,9 10,9 5,9 8,9 11,9
23. 2,3 5,3 8,3 3,3 6,3 9,3 4,3 7,3 10,3 5,3 8,3 11,3
24. 3,9 6,9 9,9 4,9 7,9 10,9 5,9 8,9 11,9 6,9 9,9 12,9
25. 3,3 6,3 9,3 4,3 7,3 10,3 5,3 8,3 11,3 6,3 9,3 12,3
26. 2,0 5,0 8,0 3,0 6,0 9,0 4,0 7,0 10,0 5,0 8,0 11,0
27. 1,2 4,2 7,2 2,2 5,2 8,2 3,2 6,2 9,2 4,2 7,2 10,2
28. 0,9 3,9 6,9 1,9 4,9 7,9 2,9 5,9 8,9 3,9 6,9 9,9
29. 0,4 3,4 6,4 1,4 4,4 7,4 2,4 5,4 8,4 3,4 6,4 9,4
30. 0,9 3,9 6,9 1,9 4,9 7,9 2,9 5,9 8,9 3,9 6,9 9,9
31. 1,0 4,0 7,0 2,0 5,0 8,0 3,0 6,0 9,0 4,0 7,0 10,0
32. 1,6 4,6 7,6 2,6 5,6 8,6 3,6 6,6 9,6 4,6 7,6 10,6
33. 1,2 4,2 7,2 2,2 5,2 8,2 3,2 6,2 9,2 4,2 7,2 10,2
34. 1,3 4,3 7,3 2,3 5,3 8,3 3,3 6,3 9,3 4,3 7,3 10,3
35. 0,7 3,7 6,7 1,7 4,7 7,7 2,7 5,7 8,7 3,7 6,7 9,7
36. 2,3 5,3 8,3 3,3 6,3 9,3 4,3 7,3 10,3 5,3 8,3 11,3
37. 1,3 4,3 7,3 2,3 5,3 8,3 3,3 6,3 9,3 4,3 7,3 10,3
38. 0,1 3,1 6,1 1,1 4,1 7,1 2,1 5,1 8,1 3,1 6,1 9,1
39. 1,8 4,8 7,8 2,8 5,8 8,8 3,8 6,8 9,8 4,8 7,8 10,8
40. 1,7 4,7 7,7 2,7 5,7 8,7 3,7 6,7 9,7 4,7 7,7 10,7
22
Продовженне таблиці Додатку 2
№ п/п |
Вариант 5 |
Вариант 6 |
Вариант 7 |
Вариант 8 |
||||||||
D1 |
D2 |
D3 |
D1 |
D2 |
D3 |
D1 |
D2 |
D3 |
D1 |
D2 |
D3 |
|
1. |
6,0 |
9,0 |
12,0 |
7,0 |
10,0 |
13,0 |
8,0 |
11,0 |
14,0 |
9,0 |
12,0 |
15,0 |
2. |
6,9 |
9,9 |
12,9 |
7,9 |
10,9 |
13,9 |
8,9 |
11,9 |
14,9 |
9,9 |
12,9 |
15,9 |
3. |
5,6 |
8,6 |
11,6 |
6,6 |
9,6 |
12,6 |
7,6 |
10,6 |
13,6 |
8,6 |
11,6 |
14,6 |
4. |
5,3 |
8,3 |
11,3 |
6,3 |
9,3 |
12,3 |
7,3 |
10,3 |
13,3 |
8,3 |
11,3 |
14,3 |
5. |
5,6 |
8,6 |
11,6 |
6,6 |
9,6 |
12,6 |
7,6 |
10,6 |
13,6 |
8,6 |
11,6 |
14,6 |
6. |
6,4 |
9,4 |
12,4 |
7,4 |
10,4 |
13,4 |
8,4 |
11,4 |
14,4 |
9,4 |
12,4 |
15,4 |
7. |
6,9 |
9,9 |
12,9 |
7,9 |
10,9 |
13,9 |
8,9 |
11,9 |
14,9 |
9,9 |
12,9 |
15,9 |
8. |
5,6 |
8,6 |
11,6 |
6,6 |
9,6 |
12,6 |
7,6 |
10,6 |
13,6 |
8,6 |
11,6 |
14,6 |
9. |
4,3 |
7,3 |
10,3 |
5,3 |
8,3 |
11,3 |
6,3 |
9,3 |
12,3 |
7,3 |
10,3 |
13,3 |
10 |
6,5 |
9,5 |
12,5 |
7,5 |
10,5 |
13,5 |
8,5 |
11,5 |
14,5 |
9,5 |
12,5 |
15,5 |
11 |
5,6 |
8,6 |
11,6 |
6,6 |
9,6 |
12,6 |
7,6 |
10,6 |
13,6 |
8,6 |
11,6 |
14,6 |
12 |
6,3 |
9,3 |
12,3 |
7,3 |
10,3 |
13,3 |
8,3 |
11,3 |
14,3 |
9,3 |
12,3 |
15,3 |
13 |
6,0 |
9,0 |
12,0 |
7,0 |
10,0 |
13,0 |
8,0 |
11,0 |
14,0 |
9,0 |
12,0 |
15,0 |
14 |
6,0 |
9,0 |
12,0 |
7,0 |
10,0 |
13,0 |
8,0 |
11,0 |
14,0 |
9,0 |
12,0 |
15,0 |
15 |
4,5 |
7,5 |
10,5 |
5,5 |
8,5 |
11,5 |
6,5 |
9,5 |
12,5 |
7,5 |
10,5 |
13,5 |
16 |
6,5 |
9,5 |
12,5 |
7,5 |
10,5 |
13,5 |
8,5 |
11,5 |
14,5 |
9,5 |
12,5 |
15,5 |
17 |
6,9 |
9,9 |
12,9 |
7,9 |
10,9 |
13,9 |
8,9 |
11,9 |
14,9 |
9,9 |
12,9 |
15,9 |
18 |
6,4 |
9,4 |
12,4 |
7,4 |
10,4 |
13,4 |
8,4 |
11,4 |
14,4 |
9,4 |
12,4 |
15,4 |
19 |
6,1 |
9,1 |
12,1 |
7,1 |
10,1 |
13,1 |
8,1 |
11,1 |
14,1 |
9,1 |
12,1 |
15,1 |
20 |
5,1 |
8,1 |
11,1 |
6,1 |
9,1 |
12,1 |
7,1 |
10,1 |
13,1 |
8,1 |
11,1 |
14,1 |
21 |
4,9 |
7,9 |
10,9 |
5,9 |
8,9 |
11,9 |
6,9 |
9,9 |
12,9 |
7,9 |
10,9 |
13,9 |
22 |
6,9 |
9,9 |
12,9 |
7,9 |
10,9 |
13,9 |
8,9 |
11,9 |
14,9 |
9,9 |
12,9 |
15,9 |
23 |
6,3 |
9,3 |
12,3 |
7,3 |
10,3 |
13,3 |
8,3 |
11,3 |
14,3 |
9,3 |
12,3 |
15,3 |
24 |
7,9 |
10,9 |
13,9 |
8,9 |
11,9 |
14,9 |
9,9 |
12,9 |
15,9 |
10,9 |
13,9 |
16,9 |
25 |
7,3 |
10,3 |
13,3 |
8,3 |
11,3 |
14,3 |
9,3 |
12,3 |
15,3 |
10,3 |
13,3 |
16,3 |
26 |
6,0 |
9,0 |
12,0 |
7,0 |
10,0 |
13,0 |
8,0 |
11,0 |
14,0 |
9,0 |
12,0 |
15,0 |
27 |
5,2 |
8,2 |
11,2 |
6,2 |
9,2 |
12,2 |
7,2 |
10,2 |
13,2 |
8,2 |
11,2 |
14,2 |
28 |
4,9 |
7,9 |
10,9 |
5,9 |
8,9 |
11,9 |
6,9 |
9,9 |
12,9 |
7,9 |
10,9 |
13,9 |
29 |
4,4 |
7,4 |
10,4 |
5,4 |
8,4 |
11,4 |
6,4 |
9,4 |
12,4 |
7,4 |
10,4 |
13,4 |
30 |
4,9 |
7,9 |
10,9 |
5,9 |
8,9 |
11,9 |
6,9 |
9,9 |
12,9 |
7,9 |
10,9 |
13,9 |
31 |
5,0 |
8,0 |
11,0 |
6,0 |
9,0 |
12,0 |
7,0 |
10,0 |
13,0 |
8,0 |
11,0 |
14,0 |
32 |
5,6 |
8,6 |
11,6 |
6,6 |
9,6 |
12,6 |
7,6 |
10,6 |
13,6 |
8,6 |
11,6 |
14,6 |
33 |
5,2 |
8,2 |
11,2 |
6,2 |
9,2 |
12,2 |
7,2 |
10,2 |
13,2 |
8,2 |
11,2 |
14,2 |
34 |
5,3 |
8,3 |
11,3 |
6,3 |
9,3 |
12,3 |
7,3 |
10,3 |
13,3 |
8,3 |
11,3 |
14,3 |
35 |
4,7 |
7,7 |
10,7 |
5,7 |
8,7 |
11,7 |
6,7 |
9,7 |
12,7 |
7,7 |
10,7 |
13,7 |
36 |
6,3 |
9,3 |
12,3 |
7,3 |
10,3 |
13,3 |
8,3 |
11,3 |
14,3 |
9,3 |
12,3 |
15,3 |
37 |
5,3 |
8,3 |
11,3 |
6,3 |
9,3 |
12,3 |
7,3 |
10,3 |
13,3 |
8,3 |
11,3 |
14,3 |
38 |
4,1 |
7,1 |
10,1 |
5,1 |
8,1 |
11,1 |
6,1 |
9,1 |
12,1 |
7,1 |
10,1 |
13,1 |
39 |
5,8 |
8,8 |
11,8 |
6,8 |
9,8 |
12,8 |
7,8 |
10,8 |
13,8 |
8,8 |
11,8 |
14,8 |
40 |
5,7 |
8,7 |
11,7 |
6,7 |
9,7 |
12,7 |
7,7 |
10,7 |
13,7 |
8,7 |
11,7 |
14,7 |
23
Продовженне таблиці Додатку 2
№ п/п |
Вариант 9 |
Вариант 10 |
Вариант 11 |
Вариант 12 |
||||||||
D1 |
D2 |
D3 |
D1 |
D2 |
D3 |
D1 |
D2 |
D3 |
D1 |
D2 |
D3 |
|
1. |
10,0 |
13,0 |
16,0 |
11,0 |
14,0 |
17,0 |
12,0 |
15,0 |
18,0 |
13,0 |
16,0 |
19,0 |
2. |
10,9 |
13,9 |
16,9 |
11,9 |
14,9 |
17,9 |
12,9 |
15,9 |
18,9 |
13,9 |
16,9 |
19,9 |
3. |
9,6 |
12,6 |
15,6 |
10,6 |
13,6 |
16,6 |
11,6 |
14,6 |
17,6 |
12,6 |
15,6 |
18,6 |
4. |
9,3 |
12,3 |
15,3 |
10,3 |
13,3 |
16,3 |
11,3 |
14,3 |
17,3 |
12,3 |
15,3 |
18,3 |
5. |
9,6 |
12,6 |
15,6 |
10,6 |
13,6 |
16,6 |
11,6 |
14,6 |
17,6 |
12,6 |
15,6 |
18,6 |
6. |
10,4 |
13,4 |
16,4 |
11,4 |
14,4 |
17,4 |
12,4 |
15,4 |
18,4 |
13,4 |
16,4 |
19,4 |
7. |
10,9 |
13,9 |
16,9 |
11,9 |
14,9 |
17,9 |
12,9 |
15,9 |
18,9 |
13,9 |
16,9 |
19,9 |
8. |
9,6 |
12,6 |
15,6 |
10,6 |
13,6 |
16,6 |
11,6 |
14,6 |
17,6 |
12,6 |
15,6 |
18,6 |
9. |
8,3 |
11,3 |
14,3 |
9,3 |
12,3 |
15,3 |
10,3 |
13,3 |
16,3 |
11,3 |
14,3 |
17,3 |
10 |
10,5 |
13,5 |
16,5 |
11,5 |
14,5 |
17,5 |
12,5 |
15,5 |
18,5 |
13,5 |
16,5 |
19,5 |
11 |
9,6 |
12,6 |
15,6 |
10,6 |
13,6 |
16,6 |
11,6 |
14,6 |
17,6 |
12,6 |
15,6 |
18,6 |
12 |
10,3 |
13,3 |
16,3 |
11,3 |
14,3 |
17,3 |
12,3 |
15,3 |
18,3 |
13,3 |
16,3 |
19,3 |
13 |
10,0 |
13,0 |
16,0 |
11,0 |
14,0 |
17,0 |
12,0 |
15,0 |
18,0 |
13,0 |
16,0 |
19,0 |
14 |
10,0 |
13,0 |
16,0 |
11,0 |
14,0 |
17,0 |
12,0 |
15,0 |
18,0 |
13,0 |
16,0 |
19,0 |
15 |
8,5 |
11,5 |
14,5 |
9,5 |
12,5 |
15,5 |
10,5 |
13,5 |
16,5 |
11,5 |
14,5 |
17,5 |
16 |
10,5 |
13,5 |
16,5 |
11,5 |
14,5 |
17,5 |
12,5 |
15,5 |
18,5 |
13,5 |
16,5 |
19,5 |
17 |
10,9 |
13,9 |
16,9 |
11,9 |
14,9 |
17,9 |
12,9 |
15,9 |
18,9 |
13,9 |
16,9 |
19,9 |
18 |
10,4 |
13,4 |
16,4 |
11,4 |
14,4 |
17,4 |
12,4 |
15,4 |
18,4 |
13,4 |
16,4 |
19,4 |
19 |
10,1 |
13,1 |
16,1 |
11,1 |
14,1 |
17,1 |
12,1 |
15,1 |
18,1 |
13,1 |
16,1 |
19,1 |
20 |
9,1 |
12,1 |
15,1 |
10,1 |
13,1 |
16,1 |
11,1 |
14,1 |
17,1 |
12,1 |
15,1 |
18,1 |
21 |
8,9 |
11,9 |
14,9 |
9,9 |
12,9 |
15,9 |
10,9 |
13,9 |
16,9 |
11,9 |
14,9 |
17,9 |
22 |
10,9 |
13,9 |
16,9 |
11,9 |
14,9 |
17,9 |
12,9 |
15,9 |
18,9 |
13,9 |
16,9 |
19,9 |
23 |
10,3 |
13,3 |
16,3 |
11,3 |
14,3 |
17,3 |
12,3 |
15,3 |
18,3 |
13,3 |
16,3 |
19,3 |
24 |
11,9 |
14,9 |
17,9 |
12,9 |
15,9 |
18,9 |
13,9 |
16,9 |
19,9 |
14,9 |
17,9 |
20,9 |
25 |
11,3 |
14,3 |
17,3 |
12,3 |
15,3 |
18,3 |
13,3 |
16,3 |
19,3 |
14,3 |
17,3 |
20,3 |
26 |
10,0 |
13,0 |
16,0 |
11,0 |
14,0 |
17,0 |
12,0 |
15,0 |
18,0 |
13,0 |
16,0 |
19,0 |
27 |
9,2 |
12,2 |
15,2 |
10,2 |
13,2 |
16,2 |
11,2 |
14,2 |
17,2 |
12,2 |
15,2 |
18,2 |
28 |
8,9 |
11,9 |
14,9 |
9,9 |
12,9 |
15,9 |
10,9 |
13,9 |
16,9 |
11,9 |
14,9 |
17,9 |
29 |
8,4 |
11,4 |
14,4 |
9,4 |
12,4 |
15,4 |
10,4 |
13,4 |
16,4 |
11,4 |
14,4 |
17,4 |
30 |
8,9 |
11,9 |
14,9 |
9,9 |
12,9 |
15,9 |
10,9 |
13,9 |
16,9 |
11,9 |
14,9 |
17,9 |
31 |
9,0 |
12,0 |
15,0 |
10,0 |
13,0 |
16,0 |
11,0 |
14,0 |
17,0 |
12,0 |
15,0 |
18,0 |
32 |
9,6 |
12,6 |
15,6 |
10,6 |
13,6 |
16,6 |
11,6 |
14,6 |
17,6 |
12,6 |
15,6 |
18,6 |
33 |
9,2 |
12,2 |
15,2 |
10,2 |
13,2 |
16,2 |
11,2 |
14,2 |
17,2 |
12,2 |
15,2 |
18,2 |
34 |
9,3 |
12,3 |
15,3 |
10,3 |
13,3 |
16,3 |
11,3 |
14,3 |
17,3 |
12,3 |
15,3 |
18,3 |
35 |
8,7 |
11,7 |
14,7 |
9,7 |
12,7 |
15,7 |
10,7 |
13,7 |
16,7 |
11,7 |
14,7 |
17,7 |
36 |
10,3 |
13,3 |
16,3 |
11,3 |
14,3 |
17,3 |
12,3 |
15,3 |
18,3 |
13,3 |
16,3 |
19,3 |
37 |
9,3 |
12,3 |
15,3 |
10,3 |
13,3 |
16,3 |
11,3 |
14,3 |
17,3 |
12,3 |
15,3 |
18,3 |
38 |
8,1 |
11,1 |
14,1 |
9,1 |
12,1 |
15,1 |
10,1 |
13,1 |
16,1 |
11,1 |
14,1 |
17,1 |
39 |
9,8 |
12,8 |
15,8 |
10,8 |
13,8 |
16,8 |
11,8 |
14,8 |
17,8 |
12,8 |
15,8 |
18,8 |
40 |
9,7 |
12,7 |
15,7 |
10,7 |
13,7 |
16,7 |
11,7 |
14,7 |
17,7 |
12,7 |
15,7 |
18,7 |
24
Продовженне таблиці Додатку 2
№ п/п |
Вариант 13 |
Вариант 14 |
Вариант 15 |
Вариант 16 |
||||||||
D1 |
D2 |
D3 |
D1 |
D2 |
D3 |
D1 |
D2 |
D3 |
D1 |
D2 |
D3 |
|
1. |
14,0 |
17,0 |
20,0 |
15,0 |
18,0 |
21,0 |
16,0 |
19,0 |
22,0 |
17,0 |
20,0 |
23,0 |
2. |
14,9 |
17,9 |
20,9 |
15,9 |
18,9 |
21,9 |
16,9 |
19,9 |
22,9 |
17,9 |
20,9 |
23,9 |
3. |
13,6 |
16,6 |
19,6 |
14,6 |
17,6 |
20,6 |
15,6 |
18,6 |
21,6 |
16,6 |
19,6 |
22,6 |
4. |
13,3 |
16,3 |
19,3 |
14,3 |
17,3 |
20,3 |
15,3 |
18,3 |
21,3 |
16,3 |
19,3 |
22,3 |
5. |
13,6 |
16,6 |
19,6 |
14,6 |
17,6 |
20,6 |
15,6 |
18,6 |
21,6 |
16,6 |
19,6 |
22,6 |
6. |
14,4 |
17,4 |
20,4 |
15,4 |
18,4 |
21,4 |
16,4 |
19,4 |
22,4 |
17,4 |
20,4 |
23,4 |
7. |
14,9 |
17,9 |
20,9 |
15,9 |
18,9 |
21,9 |
16,9 |
19,9 |
22,9 |
17,9 |
20,9 |
23,9 |
8. |
13,6 |
16,6 |
19,6 |
14,6 |
17,6 |
20,6 |
15,6 |
18,6 |
21,6 |
16,6 |
19,6 |
22,6 |
9. |
12,3 |
15,3 |
18,3 |
13,3 |
16,3 |
19,3 |
14,3 |
17,3 |
20,3 |
15,3 |
18,3 |
21,3 |
10 |
14,5 |
17,5 |
20,5 |
15,5 |
18,5 |
21,5 |
16,5 |
19,5 |
22,5 |
17,5 |
20,5 |
23,5 |
11 |
13,6 |
16,6 |
19,6 |
14,6 |
17,6 |
20,6 |
15,6 |
18,6 |
21,6 |
16,6 |
19,6 |
22,6 |
12 |
14,3 |
17,3 |
20,3 |
15,3 |
18,3 |
21,3 |
16,3 |
19,3 |
22,3 |
17,3 |
20,3 |
23,3 |
13 |
14,0 |
17,0 |
20,0 |
15,0 |
18,0 |
21,0 |
16,0 |
19,0 |
22,0 |
17,0 |
20,0 |
23,0 |
14 |
14,0 |
17,0 |
20,0 |
15,0 |
18,0 |
21,0 |
16,0 |
19,0 |
22,0 |
17,0 |
20,0 |
23,0 |
15 |
12,5 |
15,5 |
18,5 |
13,5 |
16,5 |
19,5 |
14,5 |
17,5 |
20,5 |
15,5 |
18,5 |
21,5 |
16 |
14,5 |
17,5 |
20,5 |
15,5 |
18,5 |
21,5 |
16,5 |
19,5 |
22,5 |
17,5 |
20,5 |
23,5 |
17 |
14,9 |
17,9 |
20,9 |
15,9 |
18,9 |
21,9 |
16,9 |
19,9 |
22,9 |
17,9 |
20,9 |
23,9 |
18 |
14,4 |
17,4 |
20,4 |
15,4 |
18,4 |
21,4 |
16,4 |
19,4 |
22,4 |
17,4 |
20,4 |
23,4 |
19 |
14,1 |
17,1 |
20,1 |
15,1 |
18,1 |
21,1 |
16,1 |
19,1 |
22,1 |
17,1 |
20,1 |
23,1 |
20 |
13,1 |
16,1 |
19,1 |
14,1 |
17,1 |
20,1 |
15,1 |
18,1 |
21,1 |
16,1 |
19,1 |
22,1 |
21 |
12,9 |
15,9 |
18,9 |
13,9 |
16,9 |
19,9 |
14,9 |
17,9 |
20,9 |
15,9 |
18,9 |
21,9 |
22 |
14,9 |
17,9 |
20,9 |
15,9 |
18,9 |
21,9 |
16,9 |
19,9 |
22,9 |
17,9 |
20,9 |
23,9 |
23 |
14,3 |
17,3 |
20,3 |
15,3 |
18,3 |
21,3 |
16,3 |
19,3 |
22,3 |
17,3 |
20,3 |
23,3 |
24 |
15,9 |
18,9 |
21,9 |
16,9 |
19,9 |
22,9 |
17,9 |
20,9 |
23,9 |
18,9 |
21,9 |
24,9 |
25 |
15,3 |
18,3 |
21,3 |
16,3 |
19,3 |
22,3 |
17,3 |
20,3 |
23,3 |
18,3 |
21,3 |
24,3 |
26 |
14,0 |
17,0 |
20,0 |
15,0 |
18,0 |
21,0 |
16,0 |
19,0 |
22,0 |
17,0 |
20,0 |
23,0 |
27 |
13,2 |
16,2 |
19,2 |
14,2 |
17,2 |
20,2 |
15,2 |
18,2 |
21,2 |
16,2 |
19,2 |
22,2 |
28 |
12,9 |
15,9 |
18,9 |
13,9 |
16,9 |
19,9 |
14,9 |
17,9 |
20,9 |
15,9 |
18,9 |
21,9 |
29 |
12,4 |
15,4 |
18,4 |
13,4 |
16,4 |
19,4 |
14,4 |
17,4 |
20,4 |
15,4 |
18,4 |
21,4 |
30 |
12,9 |
15,9 |
18,9 |
13,9 |
16,9 |
19,9 |
14,9 |
17,9 |
20,9 |
15,9 |
18,9 |
21,9 |
31 |
13,0 |
16,0 |
19,0 |
14,0 |
17,0 |
20,0 |
15,0 |
18,0 |
21,0 |
16,0 |
19,0 |
22,0 |
32 |
13,6 |
16,6 |
19,6 |
14,6 |
17,6 |
20,6 |
15,6 |
18,6 |
21,6 |
16,6 |
19,6 |
22,6 |
33 |
13,2 |
16,2 |
19,2 |
14,2 |
17,2 |
20,2 |
15,2 |
18,2 |
21,2 |
16,2 |
19,2 |
22,2 |
34 |
13,3 |
16,3 |
19,3 |
14,3 |
17,3 |
20,3 |
15,3 |
18,3 |
21,3 |
16,3 |
19,3 |
22,3 |
35 |
12,7 |
15,7 |
18,7 |
13,7 |
16,7 |
19,7 |
14,7 |
17,7 |
20,7 |
15,7 |
18,7 |
21,7 |
36 |
14,3 |
17,3 |
20,3 |
15,3 |
18,3 |
21,3 |
16,3 |
19,3 |
22,3 |
17,3 |
20,3 |
23,3 |
37 |
13,3 |
16,3 |
19,3 |
14,3 |
17,3 |
20,3 |
15,3 |
18,3 |
21,3 |
16,3 |
19,3 |
22,3 |
38 |
12,1 |
15,1 |
18,1 |
13,1 |
16,1 |
19,1 |
14,1 |
17,1 |
20,1 |
15,1 |
18,1 |
21,1 |
39 |
13,8 |
16,8 |
19,8 |
14,8 |
17,8 |
20,8 |
15,8 |
18,8 |
21,8 |
16,8 |
19,8 |
22,8 |
40 |
13,7 |
16,7 |
19,7 |
14,7 |
17,7 |
20,7 |
15,7 |
18,7 |
21,7 |
16,7 |
19,7 |
22,7 |
25
Приложение 3
f (t )
 1
t
2
1
t
2
e
Плотность вероятности нормального распределения 2
 2p
2p
t |
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
0, |
0,398 |
0,398 |
0,398 |
0,398 |
0,398 |
0,398 |
0,398 |
0,398 |
0,397 |
0,397 |
|
0 |
9 |
9 |
9 |
8 |
6 |
4 |
2 |
0 |
7 |
3 |
|
0, |
0,397 |
0,396 |
0,396 |
0,395 |
0,395 |
0,394 |
0,393 |
0,393 |
0,392 |
0,391 |
|
1 |
0 |
5 |
1 |
6 |
1 |
5 |
9 |
2 |
5 |
8 |
|
0, |
0,391 |
0,390 |
0,389 |
0,388 |
0,387 |
0,386 |
0,385 |
0,384 |
0,383 |
0,382 |
|
2 |
0 |
2 |
4 |
5 |
6 |
7 |
7 |
7 |
6 |
5 |
|
0, |
0,381 |
0,380 |
0,379 |
0,377 |
0,376 |
0,375 |
0,373 |
0,372 |
0,371 |
0,369 |
|
3 |
4 |
2 |
0 |
8 |
5 |
2 |
9 |
6 |
2 |
7 |
|
0, |
0,368 |
0,366 |
0,365 |
0,363 |
0,362 |
0,360 |
0,358 |
0,357 |
0,355 |
0,353 |
|
4 |
3 |
8 |
3 |
7 |
1 |
5 |
9 |
2 |
5 |
8 |
|
0, |
0,352 |
0,350 |
0,348 |
0,346 |
0,344 |
0,342 |
0,341 |
0,339 |
0,337 |
0,335 |
|
5 |
1 |
3 |
5 |
7 |
8 |
9 |
0 |
1 |
2 |
2 |
|
0, |
0,333 |
0,331 |
0,329 |
0,327 |
0,325 |
0,323 |
0,320 |
0,318 |
0,316 |
0,314 |
|
6 |
2 |
2 |
2 |
1 |
1 |
0 |
9 |
7 |
6 |
4 |
|
0, |
0,312 |
0,310 |
0,307 |
0,305 |
0,303 |
0,301 |
0,298 |
0,296 |
0,294 |
0,292 |
|
7 |
3 |
1 |
9 |
6 |
4 |
1 |
9 |
6 |
3 |
0 |
|
0, |
0,289 |
0,287 |
0,285 |
0,282 |
0,280 |
0,278 |
0,275 |
0,273 |
0,270 |
0,268 |
|
8 |
7 |
4 |
0 |
7 |
3 |
0 |
6 |
2 |
9 |
5 |
|
0, |
0,266 |
0,263 |
0,261 |
0,258 |
0,256 |
0,254 |
0,251 |
0,249 |
0,246 |
0,244 |
|
9 |
1 |
7 |
3 |
9 |
5 |
1 |
6 |
2 |
8 |
4 |
|
1, |
0,242 |
0,239 |
0,237 |
0,234 |
0,232 |
0,229 |
0,227 |
0,225 |
0,222 |
0,220 |
|
0 |
0 |
6 |
1 |
7 |
3 |
9 |
5 |
1 |
7 |
3 |
|
1, |
0,217 |
0,215 |
0,213 |
0,210 |
0,208 |
0,205 |
0,203 |
0,201 |
0,198 |
0,196 |
|
1 |
9 |
5 |
1 |
7 |
3 |
9 |
6 |
2 |
9 |
5 |
|
1, |
0,194 |
0,191 |
0,189 |
0,187 |
0,184 |
0,182 |
0,180 |
0,178 |
0,175 |
0,173 |
|
2 |
2 |
9 |
5 |
2 |
9 |
6 |
4 |
1 |
8 |
6 |
|
1, |
0,171 |
0,169 |
0,166 |
0,164 |
0,162 |
0,160 |
0,158 |
0,156 |
0,153 |
0,151 |
|
3 |
4 |
1 |
9 |
7 |
6 |
4 |
2 |
1 |
9 |
8 |
|
1, |
0,149 |
0,147 |
0,145 |
0,143 |
0,141 |
0,139 |
0,137 |
0,135 |
0,133 |
0,131 |
|
4 |
7 |
6 |
6 |
5 |
5 |
4 |
4 |
4 |
4 |
5 |
|
1, |
0,129 |
0,127 |
0,125 |
0,123 |
0,121 |
0,120 |
0,118 |
0,116 |
0,114 |
0,112 |
|
5 |
5 |
6 |
7 |
8 |
9 |
0 |
2 |
3 |
5 |
7 |
|
1, |
0,110 |
0,109 |
0,107 |
0,105 |
0,104 |
0,102 |
0,100 |
0,098 |
0,097 |
0,095 |
|
6 |
9 |
2 |
4 |
7 |
0 |
3 |
6 |
9 |
3 |
7 |
|
1, |
0,094 |
0,092 |
0,090 |
0,089 |
0,087 |
0,086 |
0,084 |
0,083 |
0,081 |
0,080 |
|
7 |
0 |
5 |
9 |
3 |
8 |
3 |
8 |
3 |
8 |
4 |
|
1, |
0,079 |
0,077 |
0,076 |
0,074 |
0,073 |
0,072 |
0,070 |
0,069 |
0,068 |
0,066 |
|
8 |
0 |
5 |
1 |
8 |
4 |
1 |
7 |
4 |
1 |
9 |
|
1, |
0,065 |
0,064 |
0,063 |
0,062 |
0,060 |
0,059 |
0,058 |
0,057 |
0,056 |
0,055 |
|
9 |
6 |
4 |
2 |
0 |
8 |
6 |
4 |
3 |
2 |
1 |
|
2, |
0,054 |
0,052 |
0,051 |
0,050 |
0,049 |
0,048 |
0,047 |
0,046 |
0,045 |
0,044 |
|
0 |
0 |
9 |
9 |
8 |
8 |
8 |
8 |
8 |
9 |
9 |
|
2, |
0,044 |
0,043 |
0,042 |
0,041 |
0,040 |
0,039 |
0,038 |
0,037 |
0,037 |
0,036 |
|
1 |
0 |
1 |
2 |
3 |
4 |
6 |
8 |
9 |
1 |
3 |
|
2, |
0,035 |
0,034 |
0,033 |
0,033 |
0,032 |
0,031 |
0,031 |
0,030 |
0,029 |
0,029 |
|
2 |
5 |
7 |
9 |
2 |
5 |
7 |
0 |
3 |
7 |
0 |
26
2, |
0,028 |
0,027 |
0,027 |
0,026 |
0,025 |
0,025 |
0,024 |
0,024 |
0,023 |
0,022 |
3 |
3 |
7 |
0 |
4 |
8 |
2 |
6 |
1 |
5 |
9 |
2, |
0,022 |
0,021 |
0,021 |
0,020 |
0,020 |
0,019 |
0,019 |
0,018 |
0,018 |
0,018 |
4 |
4 |
9 |
3 |
8 |
3 |
8 |
4 |
9 |
4 |
0 |
2, |
0,017 |
0,017 |
0,016 |
0,016 |
0,015 |
0,015 |
0,015 |
0,014 |
0,014 |
0,013 |
5 |
5 |
1 |
7 |
3 |
8 |
4 |
1 |
7 |
3 |
9 |
2, |
0,013 |
0,013 |
0,012 |
0,012 |
0,012 |
0,011 |
0,011 |
0,011 |
0,011 |
0,010 |
6 |
6 |
2 |
9 |
6 |
2 |
9 |
6 |
3 |
0 |
7 |
2, |
0,010 |
0,010 |
0,009 |
0,009 |
0,009 |
0,009 |
0,008 |
0,008 |
0,008 |
0,008 |
7 |
4 |
1 |
9 |
6 |
3 |
1 |
8 |
6 |
4 |
1 |
2, |
0,007 |
0,007 |
0,007 |
0,007 |
0,007 |
0,006 |
0,006 |
0,006 |
0,006 |
0,006 |
8 |
9 |
7 |
5 |
3 |
1 |
9 |
7 |
5 |
3 |
1 |
2, |
0,006 |
0,005 |
0,005 |
0,005 |
0,005 |
0,005 |
0,005 |
0,004 |
0,004 |
0,004 |
9 |
0 |
8 |
6 |
5 |
3 |
1 |
0 |
8 |
7 |
6 |
3, |
0,004 |
0,004 |
0,004 |
0,004 |
0,003 |
0,003 |
0,003 |
0,003 |
0,003 |
0,003 |
0 |
4 |
3 |
2 |
0 |
9 |
8 |
7 |
6 |
5 |
4 |
3, |
0,003 |
0,003 |
0,003 |
0,003 |
0,002 |
0,002 |
0,002 |
0,002 |
0,002 |
0,002 |
1 |
3 |
2 |
1 |
0 |
9 |
8 |
7 |
6 |
5 |
5 |
3, |
0,002 |
0,002 |
0,002 |
0,002 |
0,002 |
0,002 |
0,002 |
0,001 |
0,001 |
0,001 |
2 |
4 |
3 |
2 |
2 |
1 |
0 |
0 |
9 |
8 |
8 |
3, |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
3 |
7 |
7 |
6 |
6 |
5 |
5 |
4 |
4 |
3 |
3 |
3, |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
0,001 |
0,000 |
0,000 |
4 |
2 |
2 |
2 |
1 |
1 |
0 |
0 |
0 |
9 |
9 |
3, |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
5 |
9 |
8 |
8 |
8 |
8 |
7 |
7 |
7 |
7 |
6 |
3, |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
6 |
6 |
6 |
6 |
5 |
5 |
5 |
5 |
5 |
5 |
4 |
3, |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
7 |
4 |
4 |
4 |
4 |
4 |
4 |
3 |
3 |
3 |
3 |
3, |
0.000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
8 |
3 |
3 |
3 |
3 |
3 |
2 |
2 |
2 |
2 |
2 |
3, |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
9 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
