
МЕТОДИЧНІ ВКАЗІВКИ ДО РОЗРАХУНКОВИХ РОБІТ з дисципліни «Технічна діагностика автомобілів»
Введення
Поршневі двигуни автомобільні, стаціонарні і транспортні дизелі мають широке вживання. Експлуатація автомобільних двигунів носить масовий характер. Визначення технічного стану двигуна без розбирання дозволяє підвищити його надійність і поліпшити технічне обслуговування. Слід врахувати, що трудомісткість ремонту двигунів масового виробництва перевершує трудомісткість виготовлення в 5 – 10 разів. Проведення профілактичних робіт і ремонту «по стану» дає значний економічний ефект. Сучасна діагностична апаратура, що існує і розробляється останнім часом, і яка базується на останніх досягненнях науки і техніки, дозволяє з достатньою мірою точності визначати значення діагностичних параметрів, а на їх підставі оцінювати технічний стан двигунів внутрішнього згорання. При цьому значну роль має статистична інформація, отримана в процесі експлуатації двигунів. Розроблені теоретичні методи розпізнавання в технічній діагностиці і теорії інформації дозволяють шляхом обробки цієї інформації вставити точний діагноз по відомих діагностичних параметрів і ознак. У даній методичній розробці приводяться статистичний метод розпізнавання Байеса, методи статистичних рішень для одного діагностичного параметра «метод мінімального ризику» і «метод Неймана – Пірсону», метод визначення діагностичних ваг для складних m - розрядних ознак. Вживання цих методів в практиці експлуатації двигунів дозволяє значно спростити процедуру постановки діагнозу при виникненні несправності в двигуні, а також скоротити час на пошук місця і причини цієї несправності. Крім того, дозволяє прогнозувати ресурс двигуна.
Розглядаються алгоритми реалізації методів у вигляді прикладів, а також варіанти в додатку для розрахунків по цих методах. Приведені алгоритми дозволяють складати програми і проводити розрахунки на комп'ютері.
Розрахункова робота закінчується оформленням звіту, в якому відбиваються мета роботи, теоретичні відомості про метод діагностування і методичні вказівки по виконанню розрахунків.
Методична розробка призначена для використання на практичних заняттях для студентів спеціальності «Двигуни внутрішнього згорання» по дисципліні «Технічна діагностика автомобілів». Вона може використовуватися для студентів інших технічних спеціальностей, де застосовуються вказані методи для діагностування технічних систем.
Розрахункова робота № 1
Ймовірносно-статистичний метод розпізнавання Байеса
Мета роботи:
Мета роботи – знайомство з імовірнісно – статистичним методом розпізнавання Байеса і застосування його при обробці статистичної інформації, пов'язаною з постановкою діагнозу по ознаках, що проявляються, при діагностуванні двигуна.
Короткі теоретичні відомості
Розпізнавання станів здійснюють шляхом класифікації, тобто об'єкт (систему) відносять до певного класу заздалегідь відомих діагнозів по комплексу діагностичних ознак, що проявляються.
Якщо є можливість зібрати великий об'єм інформації про зв'язки ознак із станами і особливості проявів цих станів, найбільш надійним і ефективним методом розпізнавання є метод Байеса.
Метод заснований на наступному підході: якщо є діагноз D i проста ознака Kj, що зустрічається при цьому діагнозі, то вірогідність спільної появи події виражається.
Р(Di Kj )=Р(Di) Р(Кj /Di ) ( 1 )
Г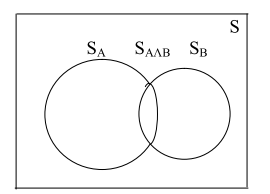 еометрична
інтерпретація методу полягає в наступному.
Передбачаємо, що є дві мішені, показані
на рисунку.
еометрична
інтерпретація методу полягає в наступному.
Передбачаємо, що є дві мішені, показані
на рисунку.
Мішень А – система станів, мішень В – система ознак. Відповідно площі цих мішеней виражаються SA і SB. При пострілах по мішенях вірогідність одночасного попадання в мішені А і В визначається
Р(АВ)= SAΛВ / S, ( 2 )
де SАВ – площа перекриття мішеней; S – загальна площа поля (куля, що летить, може з однаковою вірогідністю попасти в будь-яку точку поля).
Розділивши і помноживши праву частину попередньої рівності на величину SA отримаємо:
![]() ,
(3)
,
(3)
Позначимо SA / S =Р(А). Друге відношення площ позначимо SAΛВ /S= Р(В/А). На відміну від рівності (2) спільна площа SАВ областей А і В, сприятлива для одночасної появи подій А і В, відноситься не до всієї площі S, а лише до SA, де обов'язково реалізується подія А. Це означає, що розкид попадань при стрілянині обмежується площею SA, де подія А обов'язково відбувається, а подія В може відбуватися або не відбуватися. Вірогідність події В визначається як Р(В/А)= SАΛВ / SА.
Використовуючи отримані співвідношення, знаходимо, що вірогідність спільної появи подій
Р(АВ)= Р(А)Р(В/А) (знак кон'юнкції ^ зазвичай опускається).
Так само (розділивши і помноживши праву частину на площу SВ) отримаємо:
P(AB)=P(B)P(A/B). ( 4 )
Повертаючись до рівняння (1), доповнимо його з врахуванням отриманих співвідношень
P(D i K j)=P(D i)P(K j/D i)=P(K js)P(D i /K j) ( 5 )
Звідси витікає формула Байеса
P(D i , K j)=[P(D i) P(K j/D i)]/ P(K js), ( 6 )
де P(Di) - апріорна вірогідність діагнозу Di (визначається за статистичними даними); P(Kj/ Di) – вірогідність появи ознаки Kj в об'єктів із станом Di; P(Kjs) – вірогідність появи ознаки Kj у всіх об'єктах незалежно від їх стану (якщо із загального числа N об'єктів ознака Kj виявився в Nj об'єктів, то
P(K js) = N j / N = P(D i) P(K j/D i) , ( 7 )
де P(Kj / Di) – вірогідність діагнозу Di після того, як стала відома наявність в даного об'єкту ознаки Kj (апостеріорна вірогідність діагнозу).
Приклад використання методу Байеса.
Для практичного використання методу Байеса необхідно скласти вихідну діагностичну таблицю 1
-
Стан
Вірогідність прояву ознак
P(K 1/D i)
P( К 1/D i)
P(K 2/D i)
P( К 2/D i)
P(D i)
D1
0,1
0,9
0,8
0,2
0,1
D2
0,5
0,5
0,3
0,7
0,2
D3
0,9
0,1
0,2
0,8
0,7
Використовуючи дані таблиці, визначити вірогідність діагнозів для різних ситуацій прояву діагностичних ознак. Таких ситуацій може бути чотири:
- K1 K2 – з'явилися ознаки K1 і K2;
- K 1 K2 – ознака K1 відсутня, K2 присутня;
- K1 K2 - ознака K1 присутня, K2 відсутня;
- K1 K2 - відсутні обидві ознаки.
Для ситуації K1 K2 маємо
P(D1/ K1 K2)= 0.1* 0.8 * 0.1 =0.04
0.1* 0.8* 0.1 0.2 * 0.3* 0.5 0.7 * 0.2 * 0.9
P(D2/ K1 K2)= 0.2 * 0.3 * 0.5 =0.18
0.1* 0.8 * 0.1 0.2 * 0.3 * 0.5 0.7 * 0.2 * 0.9
P(D3/ K1 K2)= 0.7 * 0.2 * 0.9 =0.78
0.1* 0.8 * 0.1 0.2 * 0.3 * 0.5 0.7 * 0.2 * 0.9
Відмітимо, що значення всіх знаменників тут однакові, що значно спрощує розрахунки. Для ситуації K 1 K2
P(D1/ K 1 K2)=0.62
P(D2/ K 1 K2)=0.26
P(D3/ K 1 K2)=0.12
Для ситуації K1 K 2
-
P(D1 /K1
K 2)=0
P(D2/ K1
K 2)= 0.12
P(D3/ K1
K 2)= 0.88
Для ситуації K 1 K 2
P(D1 / K 1 P(D2 / K 1 P(D3 / K 1
K 2)=0.12 K 2)=0.48 K 2)=0.4
Зведемо результати розрахунків в таблицю 2
-
Стан
Ситуація
K1 K2
K 1 K2
K1 K 2
K 1 K 2
D1
0.04
0.62
0
0.12
D2
0.18
0.26
0.12
0.48
D3
0.78
0.12
0.88
0.40
Результати показують, що стану D1 найімовірніше відповідає ситуація K1 K2, стану D2 - K1 K2, стану D3 - K1 K2.
Приведений алгоритм реалізуються на ЕОМ, чим забезпечується можливість машинного діагностування. Важливо лише відстежувати апріорну (отримані на основі вихідної статистичної інформації) вірогідність в діагностичних матрицях і під час їх коректувати.
Варіанти завдань для виконання роботи по методу розпізнавання Байеса приведені в таблиці Додатка 1.
Порядок виконання роботи
1. Вивчити методичні вказівки по виконанню практичної роботи.
2. Скласти вихідну діагностичну таблицю 1.
3. Визначити вірогідність діагнозів для різних ситуацій проявів діагностичних ознак.
4. Заповнити таблицю 2.
5. Провести аналіз отриманих результатів.
6. Оформити звіт.
Розрахункова робота № 2
Визначення кордонів діагностичних інтервалів параметрів контролю технічного стану двигуна
Мета роботи
Мета роботи - придбання практичних навиків по обробці статичної інформації для діагностування двигунів.
Короткі теоретичні відомості
Ефективність діагностування двигунів в значній мірі залежить від правильного вибору параметрів (або ознак), використовуваних для оцінки технічного стану. Як правило, використовують один або декілька параметрів, які з певною достовірністю дозволяють судити про стан об'єкту контролю. Повною сукупністю параметрів слід вважати такі, які забезпечують повний контроль працездатності об'єкту. Це означає, що при відмові будь-якого його функціонального елементу у вибраній сукупності параметрів обов'язково знайдеться, принаймні, один такий, який вийде в цьому випадку за межі поля допуску. Таким чином, використовувані для діагностування параметри мають бути досить чутливими до зміни стану об'єкту, щоб формувати ознаки і діагнози передвідмовного стану або стану відмови.
У технічній діагностиці прийнято розглядати прості і складні ознаки. Простий ознаку має два стани - його наявність або відсутність. Складною ознакою (розряду m) є результат спостережень, який може бути виражений одним з m символів. Зазвичай розглядають:
- двухрозрядна ознака (m=2), що володіє двома можливими станами. Наприклад, ознака Kj відноситься до зміни параметра X, для якого встановлено два діагностичні інтервали: X <=10 і X >10, тобто К1, відповідає значенням X <= 10, а К2 відповідає значенням X > 10;
-трьохрозрядна ознака (m=3) має три можливі стани: К1; K2; K3. Наприклад, для параметра Y прийнято три діагностичні інтервали: Y<=5; 5<Y<15; Y>=15. Тоді для ознаки того, що характеризує цей параметр, можливі три значення:
К1 при Y<=5;
К2 при 5 < Y < 15; K3 при Y>=15
Одним із завдань вибору параметрів є обґрунтоване ділення безлічі його можливих значень на діагностичні інтервали, які відповідають стану об'єкту діагностування, що змінюється.
Правильне визначення діагностичних інтервалів застосованого параметра в значній мірі залежить від наявності зв'язку між станом об'єкту і значенням параметра і може бути реалізоване на підставі аналізу даних експлуатації двигуна. Міра важливості з точки зору діагностування того або іншого інтервалу вибраного параметра може бути визначена по діагностичній вазі конкретного інтервалу для даного діагнозу.
Як діагностична вага прийнята очікувана величина інформації ознаки відносно діагнозу (1):
ZD i(K j) =log 2 P(K j / Di ) (1)
P(K j )
де P(Kj/ Di) - вірогідність реалізації в інтервалі ознаки K j для об'єктів з діагнозом Di; P(Kj) - вірогідність появи Kj -ї ознаки у всіх об'єктів з різними діагнозами.
