Дифракционная решетка

Широкое распространение в науч­ном эксперименте и технике получи­ли дифракционные решетки, кото­рые представляют собой множество параллельных, расположенных на равных расстояниях одинаковых «ще­лей», разделенных равными по шири­не непрозрачными промежутками. Дифракционные решетки изготавли­ваются с помощью делительной машины, наносящей штрихи (царапи­ны) на стекле или другом прозрачном материале. Там, где проведена цара­пина, материал становится непроз­рачным, а промежутки между ними остаются прозрачными и фактически играют роль щелей.

Р ассмотрим сначала дифракцию света от решетки на примере двух ще­лей. Пусть а – ширина щели, а b – ширина непрозрачного промежутка (рис. 2.3). Расстояние между середи­нами соседних щелей называется пе­риодом решетки:

d=a+b. (2.8)

Разность хода двух крайних лучей равна:

. (2.9)

Если разность хода равна целому числу длин волн:

, (m=0, 1, 2, 3,…) (2.10)

то свет, посылаемый каждой щелью, будет взаимно усиливать друг друга. Условие интерференционных макси­мумов с учетом (2.9) имеет вид:

, (m=0, 1, 2,…) (2.11)

Это формула для главных максимумов при дифракции на дифракционной решетке.

Кроме того, в тех направлениях, в которых ни одна из щелей не распро­страняет свет, он не будет распростра­няться и при двух щелях, т. е. главные минимумы при дифракции на решетке будут наблюдаться в направлениях, определяемых усло­вием (2.3) для одной щели:

; ( =1, 2, 3,…) (2.12)

Если дифракционная решетка состо­ит из N щелей, то ус­ловием главных максимумов явля­ется, как и в случае двух щелей, соот­ношение (2.11), условием главных минимумов – соотношение (2.12), а условие дополнительных минимумов имеет вид:

, ( = 1, 2, …N-1, N+1,…2N-1, 2N+1,..) (2.13)

З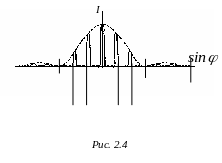 десь может принимать все це­лочисленные значения, кроме кратных числу щелей N: 0, N, 2N, .... Следовательно, в случае N щелей между двумя главными мак­симумами располагается (N–1) дополнительных мини­мумов, разделенных вторичными максимума­ми, создающими относительно сла­бый фон.

Рис. 2.4 даёт представление о распределении интенсивности при дифракции на решётке. Положение главных максимумов зависит от длины волны λ. Поэтому при пропускании через решетку бело­го света все максимумы, кроме цент­рального, разлагаются в спектр, фи­олетовый конец которого обращен к центру дифракционной картины, а красный – наружу. Таким образом, дифракционная решетка представля­ет собой спектральный прибор. Заме­тим, что в то время как стеклянная призма сильнее всего отклоняет фи­олетовые лучи, дифракционная ре­шетка, наоборот, сильнее отклоняет красные лучи.

Экспериментальная часть

Приборы и оборудование: гелий-неоновый ла­зер, ди­ф­рак­ци­он­ная ре­шет­ка, содержащая 50 штрихов/мм.

Экспериментальная установка

Принципиальная схема лабораторной установки представлена на рис. 2.5.

Методика измерений

М е­то­ди­ка из­ме­ре­ния дли­ны во­л­ны мо­но­хро­ма­ти­че­с­ко­го из­лу­че­ния, ка­ко­вым яв­ля­ет­ся ла­зер­ное, со­сто­ит в ис­сле­до­ва­нии кар­ти­ны, полу­ча­е­мой по­с­ле про­хо­ж­де­ния из­лу­че­ния че­рез ди­ф­рак­ци­он­ную ре­шетку. Оп­ре­де­ляя на ди­ф­рак­ци­он­ной кар­ти­не рас­сто­я­ние x ме­ж­ду двумя симметричными глав­ны­ми ма­к­си­му­ма­ми раз­ных по­ряд­ков и из­ме­ряя рас­сто­я­ние от ди­ф­рак­ци­он­ной ре­шет­ки до эк­ра­на, мо­ж­но лег­ко най­ти дли­ну во­л­ны ла­зер­но­го из­лу­че­ния. Для угла дифракции φ (рис.2.5) получим:

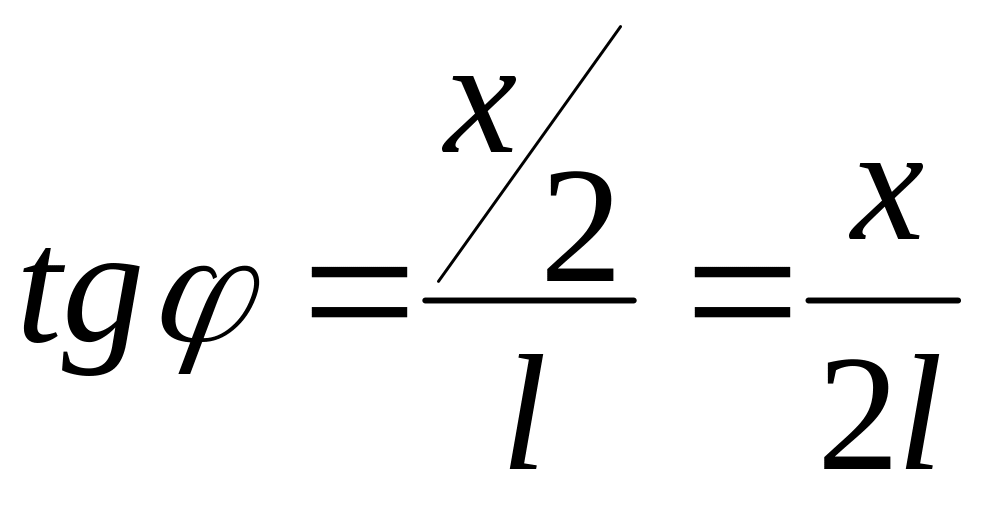. (2.14)

Из (2.11) получим:

. (2.15)

Период дифракционной решётки, которая используется в данной работе, d=0.02 мм.

Внимание!

1. Ра­бо­тая с ла­зе­ром, ПО­М­НИ­ТЕ, что на элек­т­ро­ды га­зо­раз­ряд­ной труб­ки по­да­ет­ся ОПА­С­НОЕ ДЛЯ ЖИЗ­НИ вы­со­кое на­пря­же­ние.

2. По­па­да­ние ла­зер­но­го из­лу­че­ния на сет­чат­ку гла­за вы­зо­вет не­про­дол­жи­тель­ное ос­ле­п­ле­ние или бо­лее серь­ез­ные не­при­ят­но­сти.