Теоретическое вве­де­ние

Дифракцией называется отклонение волн от прямолинейного распространения при их взаимодействии с препятствием. Дифракция наблюдается для волн любой природы. Благодаря дифракции волны могут попадать в область геометрической тени: звук слышен за углом дома, радиоволны могут распространяться далеко за пределы прямой видимости антенны передатчика, а в центре тени от освещенного диска наблюдается светлое пятно.

Необходимым условием наблюдения дифракции является соизмеримость длины волны с размерами препятствия. Так, например, мы не можем видеть, что происходит за углом дома, но можем слышать: потому что длина волны света много меньше размеров препятствия (λ≈5^.10^-7м<<l), а длина волны звука – того же порядка.

При дифракции (как и при интерференции) происходит перераспределение ин­тенсивности в результате суперпозиции волн. В сущности, между дифракцией и ин­терференцией нет принципиальных различий: по историческим причинам суперпо­зицию конечного числа волн называют интерференцией, а суперпозицию бесконеч­ного числа волн – дифракцией.

Для анализа распространения света Гюйгенс предложил простой метод, названный впоследствии принципом Гюйгенса: каждая точка волнового фронта является вторичным точечным источником сферических волн. Волновой фронт – это совокупность точек пространства, до которых дошла волна к данному моменту времени.

Французский физик О. Фре­нель дополнил этот принцип. В соответствии с принципом Гюйгенса-Френеля:

1. Каждый элемент поверхности волнового фронта служит источником вторичной сферической волны, амплитуда которой пропорциональна площади элемента.

2. Все вторичные источники когерентны и излучают в одной и той же фазе, если расположены на одной и той же волновой поверхности.

3. Вторичные источники излучают преимущественно в направлении нормали к волновому фронту.

Дифракция на щели

Пусть на бесконечно длинную щель падает плоская световая волна. В соответствии с принципом Гюйгенса-Френеля освещенную щель можно рассматривать как множест­во точечных когерентных источников волн. Поместим за щелью экран, расстояние до которого достаточно велико по сравнению с шириной ще­ли. Это условие означает, что в дан­ную точку Р экрана попадет парал­лельный пучок лучей, отклонившийся на угол φ (рис. 2.1). Оптическая разность хода АС=Δ крайних лучей из этого пуч­ка определяется из треугольника ABC ( ):

, (2.1)

где а=АВ – ширина щели. Разобьем щель на зоны Френеля, параллельные щели: оптическая разность хода лучей, идущих от соседних зон, равна половине длины волны, то есть колебания в них происходят в противофазе. Если при наблюдении из точки Р в щели по­мещается четное число зон Френеля:

, (2.2)

то их вклады взаимно погасятся и в точке Р будет наблюдаться минимум интенсивности света. Та­ким образом, из (2.1) и (2.2) получим условие дифракционных минимумов при дифракции на щели:

; (m=1, 2, 3,…) (2.3)

где угол – направление на минимум с номером m.

Если разность хода крайних лучей равна нечетному числу полуволн:

, (2.4)

то при наблюдении из точки Р в щели помещается нечетное число зон Френеля. Каждая зона га­сит соседнюю, а оставшаяся послед­няя посылает свет в направлении и образует максимум. Поэтому условие максимумов имеет вид:

; (m=1, 2, 3,…) (2.5)

Соображения, приводящие к выра­жениям (2.3) и (2.5), имеют, вооб­ще говоря, приближенный характер, поскольку мы применили метод зон Френеля для бесконечно удаленных точек наблюдения, рассматривая диф­ракцию в параллельных лучах, однако условие ми­нимумов (2.3) оказывается точным.

Что же касается «центральной» точ­ки О экрана, расположенной против центра щели, то в нее попадает пучок неотклонённых лучей, ортогональных щели. Все они имеют одинаковую фа­зу, т. е. должны усиливать друг друга. Поэтому в условии минимумов (2.3) исключено значение m=0, соответст­вующее точке О.

Значение m=0 исключено и из ус­ловия максимумов (2.5), поскольку этот максимум должен был бы расположиться между центральным максимумом и первым ми­нимумом, что невозможно.

Точные расчёты показывают, что при наложении всех вторичных волн, идущих под углом  от каждой точки щели, с учётом их амплитуд и фаз, амплитуда результи­рующего колебания имеет вид:

. (2.6)

Для точки О, лежащей против центра щели, угол φ=0 и А_φ=А₀. Этот ре­зультат следует, как мы видели, и из физических рассуждений. Сле­дующий за ним первый максимум можно найти при решении уравнения , что даёт:

. (2.7)

И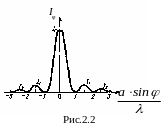 з приближенного выражения (2.5) при m=1 следует коэффициент 1.5 вместо правильного 1.43, что приво­дит к погрешности всего лишь в 5%. Для других максимумов согласие с приближенной формулой стано­вится еще лучше. При углах φ, удовлетворяющих ус­ловию (m=1, 2, 3, ...), амплитуда , как видно из (2.6), равна нулю. Это условие определяет положение минимумов, как и было получено выше в (2.3). На рис.2.2 представлена зависимость интенсивности света от угла дифракции.