Кон­т­роль­ные во­п­ро­сы

1. Что та­кое внешний фо­то­электрический эф­фект?

2. Объ­я­с­ни­те ус­т­рой­ст­во и прин­цип дей­ст­вия фо­то­эле­мен­та.

3. Нарисуйте вольтамперную характеристику фотоэлемента.

4. Сфор­му­ли­руй­те основные за­ко­ны фо­тоэф­фе­к­та.

5. В чём состоит невозможность объяснения законов внешнего фотоэффекта в волновой оптике? Изложите гипотезу Эйнштейна о фотонах.

6. Получите урав­не­ние Эйн­штей­на для фотоэффекта; объясните его смысл.

7. Что та­кое «кра­с­ная грани­ца» фо­то­эф­фе­к­та? Запишите выражение для красной границы.

8. Что по­ка­зы­ва­ет ин­те­граль­ная чув­ст­ви­тель­ность фо­то­эле­мен­та?

Используемая ли­те­ра­ту­ра

[1] §§ 36.1, 36.2;

[2] § 28.2;

[3] § 4.6;

[6] § 8;

[7] §§ 202-204.

Лабораторная работа 3-08 Изучение спектра водорода и определение постоянной Ридберга

Цель работы: из­ме­ре­ние длин волн спек­т­раль­ных ли­ний се­рии Бальмера, оп­ре­де­ле­ние по­сто­ян­ных Рид­бер­га и План­ка.

Теоретическое введение

Модели атома Томсона и Резерфорда. Трудности ядерной модели.

В 1903 г. Томсон предложил модель атома, согласно которой атом представляет собой равномерно заполненную положительным зарядом сферу, внутри которой находится электрон. Суммарный положительный заряд сферы равен суммарному заряду электронов, так что атом в целом нейтрален. Электрон, выведенный из положения равновесия, совершает колебания под действием кулоновских сил. Однако в дальнейшем выяснилась несостоятельность этой модели.

Для того чтобы выяснить характер распределения положительных и отрицательных зарядов в атоме, было необходимо непосредственное опытное «зондирование» внутренних областей атома. Такое зондирование осуществили Резерфорд и его сотрудники с помощью α-частиц, наблюдая их рассеяние при прохождении через тонкую металлическую фольгу.

Оказалось, что некоторое количество α-частиц рас­сеивается на очень большие углы (почти до 180⁰). Столь сильное отклонение α-частиц возможно только в том случае, если внутри атома имеется чрезвычайно сильное электрическое поле, которое соз­дается зарядом, связанным с большой массой и сконцентрированным в очень малом объеме. Основываясь на этом выводе, Резерфорд предложил в 1911 г. ядерную модель атома. Согласно предположению Резерфорда, атом представляет собой систему зарядов, в центре которой расположено тяжелое положительное ядро с зарядом Ze, имеющее размеры, не превышающие 10^-14 м, а вокруг ядра расположены Z электронов, распределенных по всему объему, занимаемому атомом. Почти вся масса атома сосредоточена в ядре.

Весь положительный заряд атома сосредоточен в его ядре – области, занимающей весьма малый объем по сравнению со всем объемом атома. Рассея­ние α-частицы на таком малом объекте маловероятно, поэтому большинство α-частиц испытывает незначительное рассе­яние; α-частицы, проходящие вблизи от ядра, испытывают резкие отклонения, так как на малых расстояниях силы отталкивания между положительно заряженными α-частицей и ядром должны быть очень велики. Вероятность попаданий α-частиц в ядро и их отклонений на боль­шие углы сравнительно мала, но не равна нулю.

Поскольку система неподвижных зарядов не может находиться в устойчивом состоянии, Резерфорду пришлось отказаться от статической модели атома и предположить, что элек­троны движутся вокруг ядра, опи­сывая замкнутые траектории. Модель часто называют планетар­ной, по аналогии с Солнеч­ной системой: в центре системы находится «солнце» – ядро, а вокруг него по орбитам движутся «планеты» – электроны.

Однако ядерная мо­дель оказалась в противоречии с законами классиче­ской механики и электродинамики. Электрон по орбите будет дви­гаться с ускорением, в связи с чем, согласно классической электродинамике, он должен не­прерывно излучать электромагнитные (световые) волны. Процесс излучения сопровождается потерей энергии, так что электрон должен в ко­нечном счете упасть на ядро. Атом Резерфорда оказался неустойчивой системой, что противоречит опыту.

Далее, модель Резерфорда не могла объяснить линейчатый характер спектров атомов. Из модели следовало, что электромагнитное излучение атома имеет непрерывный, а не линейчатый спектр, так как электрон не удерживается на круговой орбите, а по спирали приближается к ядру, и частота его обращения вокруг ядра (а следовательно, и частота излучаемых им электромагнитных волн) непрерывно изменяется.

Линейчатый спектр атома водорода.

А томы поглощают и испускают свет только определённой длины волны, причём спектральные линии группируются в серии (на рис.8.1 приведён спектр водорода).

Для спектра водорода, простейшего из атомов, была установлена (не выведена, а угадана!) несложная формула

. (8.1)

Здесь λ – длина волны излучения, n и k (k<n) – целые числа, а R – постоянная Ридберга (R=1.1^.10⁷ м^-1). Оказалось, что серия Лаймана (см. рис.8.1) получается при k=1, n=2, 3, 4, …∞; серия Бальмера (она наблюдается в видимой области спектра) – при k=2, n=3, 4, 5, …∞; серия Пашена – при k=3, n=4, 5, 6, …∞ и так далее.

Теория Бора атома водорода и водородоподобных ионов

Первая попытка построения неклассиче­ской теории атома была предпринята Бором (1913) и составила важный этап в развитии современной физики. В основе этой теории лежала идея связать в единое целое эмпи­рические закономерности линейчатых спек­тров, ядерную модель атомов Резерфорда и квантовый характер излучения и поглоще­ния света, подтвержденные обширным эк­спериментальным материалом. В теории Бо­ра не содержалось принципиального отказа от описания поведения электрона в атоме при помощи законов классической физики. Однако классиче­ское описание дополнялось некоторыми огра­ничениями, накладываемыми на возможные состояния электронов в атоме. Эти ограни­чения были сформулированы в виде посту­латов, физический смысл которых не мог быть объяснен в рамках теории, но, более того, противоречил сохраняющемуся в теории классическому описанию движения электрона в атоме. Тем не менее, такой принципиально непоследовательный путь привел к правильным результатам в некото­рых вопросах. Теория Бора базировалась на следующих постулатах:

Постулат стационарных состояний:

1. Электрон в атоме может находится только на стационарной орбите; при этом он не излучает и не поглощает энергии. Круговые стационарные орбиты определяются условием квантования момента импульса :

. (n=1, 2, 3,…∞) (8.2)

Здесь n – номер орбиты, =1.05^.10^-34Дж^.с – постоянная Планка, m – масса электрона, v и r – скорость электрона на орбите соответствующего радиуса.

Правило частот:

2. Излучение энергии атомом происходит только при переходе электрона с одной орбиты (n) на другую (k<n). При переходе с одной стационарной орбиты на другую электрон излучает (поглощает) квант света с частотой ν и энергией hν, равной разности энергий стационарных состояний, между которыми произошел переход:

. (8.3)

Этот постулат отражает закон сохранения энергии и гипотезу Планка-Эйнштейна о квантах.

Рассмотрим электрон, движущийся в поле атомного ядра с зарядом Ze. При Z=1 такая система соответствует атому водорода, при иных Z – водородоподобному иону, т.е. атому с порядковым номером Z, из которого удалены все электроны, кроме одного (рис.8.2). По второму закону Ньютона произведение массы электрона на его центростремительное ускорение должно равняться кулоновской силе притяжения электрона к ядру:

. (8.4)

Из (8.2) и (8.4) получим:

; (8.5)

. (8.6)

После подстановки (8.5) в (8.6) и сокращения:

;

можно найти радиус орбиты с номером n:

. (8.7)

Таким образом, радиус электронных орбит в атоме может принимать лишь ряд дискретных значений. Для первой орбиты атома водорода а₀≡ r₁=53 пм – первый Боровский радиус.

Энергия атома слагается из кинетической энергии электрона (ядро неподвижно) и потенциальной энергии взаимодействия электрона с ядром:

. (8.8)

Из (8.6) следует, что кинетическая энергия , тогда

. (8.9)

Подставив в (8.9) радиус орбиты (8.7), получим дозволенные значения энергии атома E_n:

, (8.10)

где n=1, 2, 3,…∞.

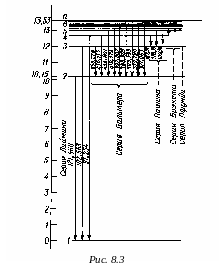
Схема энергетических уровней, определяемых (8.10), дана на рис.8.3.

Состояние с минимальной энергией (n=1) называется основным. Тогда энергия электрона в атоме водорода равна Е₁=–13.6 эВ. Электрон не связан с ядром, когда n→∞, Е_∞=0. Таким образом, энергия ионизации атома водорода из основного состояния равна:

E_И=(Е_∞–Е₁)=13.6 эВ.

При переходе атома водорода из состояния n в состояние k в соответствии со вторым постулатом Бора (8.3) испускается квант с энергией

. (8.11)

Тогда для длины волны излучения:

, (8.12)

где с – скорость света. Сравнив (8.1) и (8.12), получим значение постоянной Ридберга (для водорода Z=1):

. (8.13)

После подстановки значений величин получим . Таким образом, теория Бора позволила также вычислить постоянную Ридберга.

Трудности теории Бора. Совпадение выводов теории Бора с опытными данными для водорода оказалось идеальным. Однако наряду с успехами в теории Бора обнаружились существенные недостатки. Главнейшим из них была внутренняя логическая противоречивость теории: она не была ни последовательно классической, ни последовательно квантовой теорией. В ряде проблем теория Бора привела к существенным трудностям. Наиболее серьёзной неудачей явилась абсолютная невозможность создать теорию атома гелия, содержащего помимо ядра два электрона.

Теория Бора оказалась лишь переходным этапом на пути создания после‑ довательной теории атомных и ядерных явлений. Такой последовательной теорией явилась квантовая механика. Применение её к атомным процессам позволило не только объяснить многообразие явлений атомной и ядерной физики, но и вскрыть физическое содержание самих постулатов Бора.

Водородоподобная система в квантовой механике

Состояние микрочастицы описывается в квантовой ме­ханике волновой функцией ψ. Она является функцией координат и времени. Квадрат модуля волновой функции определяет вероятность dP того, что частица будет обнаружена в пределах объема dV:

. (8.14)

Волновая функция может быть найдена путем решения уравнения Шрёдингера:

. (8.15)

Здесь Δ – оператор Лапласа ( ); U –потенциальная энергия частицы. Уравнение Шрёдингера является основным уравнением квантовой механики. Подобно тому, как уравнения динамики Ньютона не могут быть получены теорети­чески, а представляют собой обобщение большого числа опытных фактов, уравнение Шрёдингера также нельзя вывести из каких-либо известных ранее соотношений. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем обстоятельством, что все вытекающие из него следствия самым точным образом согласуются с опытными фактами.

В атоме водорода или водородоподобном ионе потенциальная энергия электрона равна:

. (8.16)

Уравнение Шрёдингера имеет в этом случае вид:

. (8.17)

Можно показать, что (8.17) имеет однозначные, конечные и непрерывные решения в следующих случаях: 1) при любых положительных значениях Е; 2) при дискретных отрицательных значениях энергии, равных:

, (n=1, 2, 3,…∞). (8.18)

Случай Е>0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся вновь на бесконечность. Случай Е<0 соответствует электрону, находящемуся в пределах атома. Сравнение (8.18) и (8.10) показывает, что квантовая механика приводит к таким же значениям энергии водородного атома, какие получались и в теории Бора. Однако в квантовой механике эти значения получаются логическим путём при решении уравнения Шрёдингера. Бору же для получения такого результата пришлось вводить специальные дополнительные предположения.