2.2.2 Построение диаграммы изменения аналога скорости (чертёж)

Под диаграммой аналога ускорений (ускорений) получаем графическим интегрированием диаграмму изменения аналога скорости (скорости) в зависимости от угла поворота кулачка (в зависимости от времени).

Для этого:

1. Строим на диаграмме аналогов ускорений (ускорений) ординаты аа', бб', вв', …, соответствующие серединам интервалов 1-2, 2-3, 3-4, … на оси (t), до пересечения с графиком. Из точек а,б,в, … опустим перпендикуляры а'а, б'б, в'в … на ось d²S/d².

2. На продолжении оси (t) и на расстоянии (K₂О) = 40 мм от начала отсчета выбираем точку К₂ и соединяем ее с точками А,Б,В;

3. На графике аналога скоростей (скоростей) из точки 1 проводим отрезок (хорду) 1-2' в интервале 1-2 по оси угла поворота кулачка  (времени одного оборота кулачка t), параллельный К₂A; отрезок 2'-3', в интервале 2-3, параллельный лучу К₂A; отрезок 3'-4', параллельный лучу К₂Б, в интервале 3-4 и так далее. Полученные точки 1',2',3', … соединяем плавной линией.

Замечание: точки 9'-10'-11'-12'-1' соединяем прямыми линиями, так как на диаграмме аналога ускорения (ускорения) значения аналога ускорений на интервалах 9-10-11-12-1 были постоянны.

2.2.3 Построение диаграммы перемещения (чертёж)

Аналогично, интегрируя диаграмму аналога скорости (скорости) dS/d=f() (dS/dt=f(t)) в зависимости от угла поворота кулачка (в зависимости от времени), строим диаграмму перемещения ведомого звена в зависимости от угла поворота кулачка (в зависимости от времени). (К₁О) = 40 мм.

Необходимо, так же отметить, что перпендикуляры из середин интервалов на оси угла поворота кулачка  обязательно восстанавливать до пересечения с кривой графика dS/d=f(), (); dS/dt=f(t), (t).

На построенной диаграмме перемещения толкателя находим угол удаления ( ), угол возвращения ( ), угол дальнего стояния (_. ), угол ближнего стояния ( ) На диаграмме S=f(), (S=f(t)) находим максимальную ординату h_max, соответствующую максимальному ходу толкателя H. Зная h_max и H, можно определить масштабные коэффициенты диаграммы перемещений толкателя:

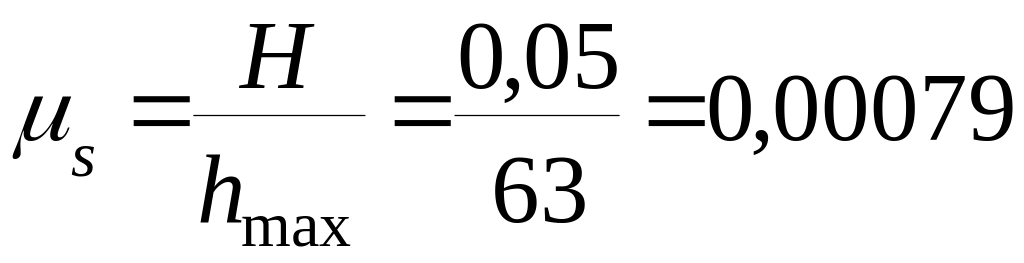м/мм

Масштаб скорости на диаграмме аналога скорости (скорости) равняется:

;

Масштаб аналога скорости найдем по формуле:

;

Масштабный коэффициент ускорений на диаграмме ускорений:

;

Масштаб аналога ускорения равен:

;

2.3 Определение минимального радиуса профиля кулачка (чертёж)

Определяем минимальный радиус теоретического профиля кулачка с помощью совмещенной диаграммы S=f(dS/d), учитывая максимально допустимый угол давления.

Строим диаграмму S=f(dS/d).

На вертикальной оси координат откладываем вверх от начала отсчета отрезки 1-2'', 1-3'',1-4'' …, равные отрезкам 2-2'', 3-3'', 4-4'' … на диаграмме перемещений толкателя. Из точек 2'',3'',4'' … восстанавливаем перпендикуляры к оси перемещений толкателя, на которых откладываем отрезки 2''-2', 3''-3', 4''-4', … равные отрезкам 2-2', 3-3', 4-4', … на диаграмме аналога скоростей (скоростей), помноженным на , для соблюдения единого масштаба совмещенной диаграммы S=f(dS/d).

Точки 1,2,3,…11,12 соединяем плавной кривой. Получили диаграмму S=f(dS/d).

Справа и слева от оси строим максимально допустимый угол давления так, чтобы одна сторона угла была касательной к диаграмме S=f(dS/dj), а вторая параллельна оси S.

На расстоянии e'=e/_s мм (e' = 12,658 мм) от оси S проводим прямую параллельную оси перемещений S. На пересечении этой прямой с правой касательной получаем точку T₂, соединяя которую с точкой 1, получим минимальный радиус профиля кулачка.