1.3 Силовой расчет механизма

1.3.1 Определение параметров и построение расчётной схемы

Силовой расчет проводится для выбранного (для которого строили план ускорений) положения механизма, для этого: изображаем группу Ассура (звенья 2 и 3) из плана положений, прикладываем в соответствующие точки соответствующие силы (рисунок 10)

Масштабный коэффициент для кинематической схемы к-к механизма:

м/мм

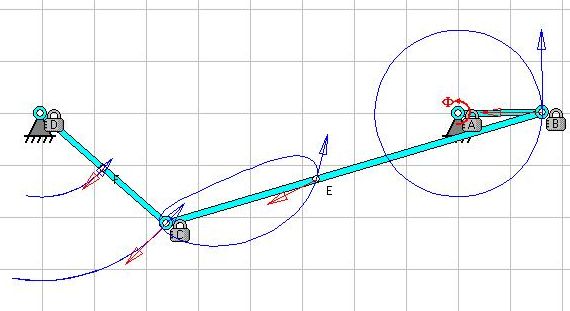
Рис. 12. Кинематическая схема кривошипно-коромыслового механизма (положение/позиция 17) в программе Roberts Animator

G₂ – сила тяжести 2-го звена, то есть шатуна.

P_и2 – сила инерции второго звена, направлена против ускорения цен­тра тяжести 2-го звена (по 2 закону Ньютона).

G₃ – сила тяжести 3-го звена, коромысла.

P_и3 – сила инерции 3-го звена, направлена против ускорения цен­тра тяжести 3-го звена.

P_п.с. – сила полезного сопротивления.

R₄₃ – реакция 4-го звена на 3-е приложена к т. D, раскладывается на две составляющие неиз­вестной реакции опоры: и .

R₁₂ – реакция 1-го звена на 2-е приложена к т. В, раскладывается на две составляющие неиз­вестной реакции опоры: и . Индексы у указанных физических параметров отражают нумерацию звена. 1 – кривошип, 2 – шатун, 3 – коромысло, 4 опора.

Найдем массы звеньев 2 и 3.

Силы инерции звеньев 2 и 3.

Значения ускорений берем из таблиц Excell для конкретной точки и конкретного положения. Следует иметь в виду, что в таблицах данные представлены в мм/с². В расчетные формулы данные следует вставлять в в метрах.

Чтобы рассчитать силы , и моменты M_u2 , M_u3 можно воспользоваться принципом Даламбера: «Если остановить движущуюся систему звеньев в определенный момент времени и приложить все действую­щие силы, включая силу инерции, то такую систему можно решать в статике».

Рассчитаем угловое ускорение второго звена:

Здесь (СВ) – длина вектора , на плане ускорений в мм.

Геометрический момент инерции:

I₂=0,1m₂×l_BC²=0,1×7,14× (0,75)²=0,402 кг×м²

Момент инерции:

M_u2=₂×I₂=1248×0,402=501,696 Н×с

Определим величину тангенциальной составляющей неизвестной ре­акции опоры , для этого запишем уравнения моментов всех сил, действующих на звенья относительно центра вращательной опоры С:

Знак минус означает, что первоначально направление силы было выбрано неверно, поэтому на плане сил будем ее строить в обратном направлении. Аналогично найдем силу :

Рассчитаем угловое ускорение третьего звена:

Здесь (СD) – длина вектора , на плане ускорений в мм.

Геометрический момент инерции:

I₃=0,1m₃×l_CD²=0,1×5,10× (0,32)²= 0,0522 кг×м²

Момент инерции:

M_u3=₃×I₃=1891,625×0,0522= 98,74 Н×с

Определим величину тангенциальной составляющей неизвестной ре­акции опоры , для этого запишем уравнения моментов всех сил, действующих на звенья относительно центра вращательной опоры С:

1.3.2 Построение плана сил

Выберем масштабный коэффициент плана сил:

Длину вектора силы выбираем произвольно.

План сил строится из векторного уравнения:

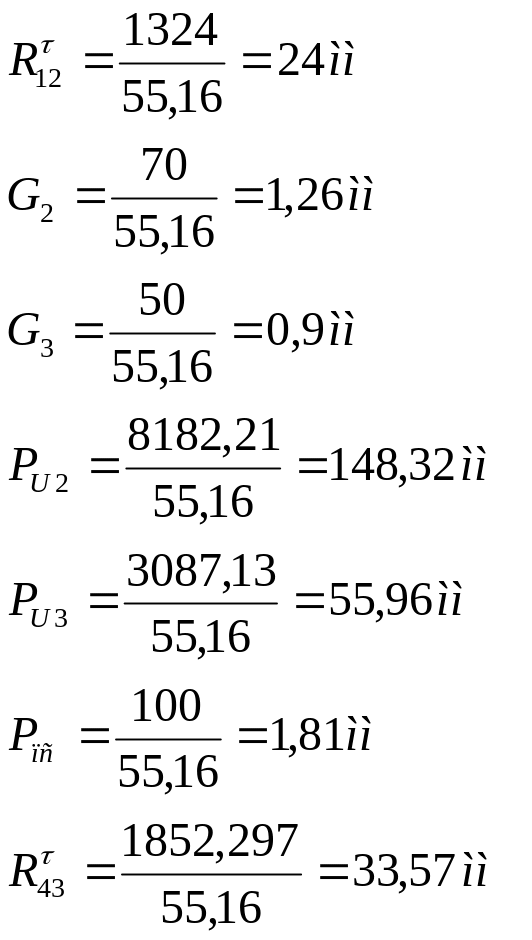
Строим силы в соответствии с векторным уравнением. Из полюса плана сил проводим отрезок R^₁₂ в масштабе _F. Строим остальные известные силы (G₂, G₃, P_u2, P_пс, P_u3, R^₄₃), присоединяя вектор каждой из них к концу вектора предыдущей силы. Для определения силы Rⁿ₁₂ прово­дим отрезки и .Из точки пересечения Rⁿ₁₂ и Rⁿ₄₃ строим ре­зультирующую силу R₁₂, начало которой в точке пересечения сил Rⁿ₄₃ и Rⁿ₁₂, а конец попадает в начало вектора G₂.

Сила реакции первого звена на второе:

R₁₂= 123 мм  55,167 Н/мм = 6785,541 Н

Рисунок 11 –