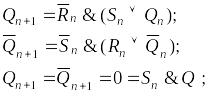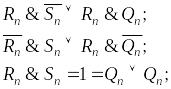3. Асинхронные триггеры

   1. Асинхронный rs-триггер

Асинхронный RS-триггер является двухвходовым триггером с раздельным управлением по каждому входу: при подаче активного сигнала на S –вход триггер устанавливается в единичное состояние, активный сигнал на входе R приводит к возврату триггера в нулевое состояние.

На рис. 1.7 приведены две схемы RS-триггеров, построенные в базисе ИЛИ-НЕ. Активными входными сигналами, переключающими триггер, являются единицы. Здесь же приведено условное обозначение триггера. Если S = 1, а R = 0, на выходах триггера появятся сигналы:

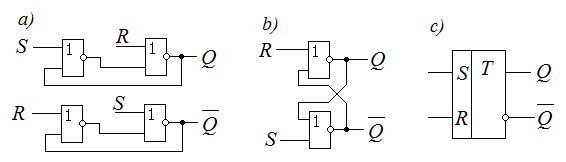
Рис. 1.7. Схема RS-триггера в базисе ИЛИ-НЕ

a, b – варианты триггерных схем, с – условное обозначение

Если же S = 0, а R = 1, значения сигналов на выходах будут противоположными. Если на обоих входах нули, триггер сохраняет ранее установленное состояние. Подача на оба входа единиц приведёт к появлению на обоих выходах нулей. После одновременного снятия единиц с входов триггер перейдёт в одно из устойчивых состояний нулевое или единичное.

В табл. 1.2 приведены переходы триггера из одного состояния в другое. При этом скобками отмечены устойчивые состояния триггеров, стрелки показывают переходы из неустойчивых состояний в устойчивые. Значком Ø отмечены неопределённые состояния триггера.

Примечание. Неопределенные состояния считаются запрещенными, допускается только кратковременная подача единиц на оба входа, например, на время отпускания якоря обесточенного реле.

Таблица 1.2

Таблица состояний асинхронного RS-триггера в базисе ИЛИ-НЕ

tn				tn+1	tn				tn+1
Набор	Входные переменные		Тек. сост.	Нов. сост.	Набор	Входные переменные		Тек. сост.	Нов. сост.
	Rn	Sn	Qn	Qn+1		Rn	Sn	Qn	Qn+1
0	0	0	0	(0)	4	1	0	0	(0)
1	0	0	1	(1)	5	1	0	1	0
2	0	1	0	1	6	1	1	0	Ø
3	0	1	1	(1)	7	1	1	1	Ø

Метод непосредственного решения функций алгебры логики.

На рис. 1.8 карты Карно: эталонная и для Q_n+1.

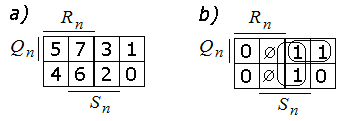
Рис. 1.8. Карты Карно RS-триггера,

построенного в базисе ИЛИ-НЕ

1. – эталонная карта Карно, b) – карта Карно для Q_n+1

Поскольку триггер может находиться в неопределенном состоянии, функции алгебры логики должны описывать оба выхода триггера.

Используя карту Карно, не трудно составить функции алгебры логики, описывающие работу RS-триггера в базисе ИЛИ-НЕ:

(1.1)

Если , на обоих выходах триггера будут нули, что приведет триггерную схему в неопределенное состояние.

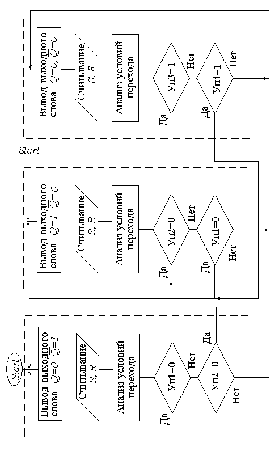
Алгоритм вычисления этих ФАЛ приведен на рис.1.9.

Рис. 1.9. Алгоритм непосредственного решения ФАЛ

при моделировании RS–триггера, построенного в базисе ИЛИ. НЕ.

Использование графа состояний для разработки алгоритма модели

На рис. 1.10 изображен граф состояний RS–триггера, построенного в базисе ИЛИ. НЕ.

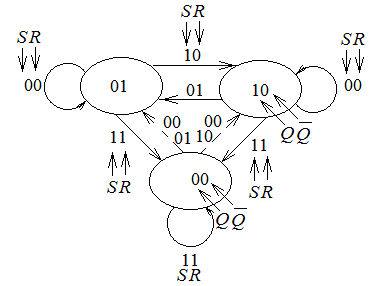
Рис. 1.10. Граф RS-триггера, построенного в базисе ИЛИ-НЕ

Рис. 1.11. Алгоритм моделирования RS – триггера, построенного в базисе ИЛИ-НЕ

Триггер может находиться в одном из трех состояний. Нижнее состояние является неустойчивым, в него переходит триггер при подаче на оба входа единиц. Появление на входах 01 или 10 приводит к переходу триггера в соответствующее устойчивое состояние. Если триггер находится в неустойчивом состоянии и на обоих входах одновременно появились нули, переход триггера в первое или второе состояние не предсказуем.

Алгоритм рассматриваемого триггера представляет собой три модуля, предусматривающих вывод состояния триггера, ввод входных переменных и решение функций алгебры логики, описывающих условия перехода триггера из одного состояния в другое (рис. 1.11).

Условия перехода:

Использование таблиц переходов и выходов при разработке модели

Использование таблиц переходов и выходов позволяет разработать интерпретирующую программу. В этом случае программа будет универсальной, не зависящей от схемы устройства.

Таблица 1.3.

Таблица переходов RS – триггера в базисе ИЛИ-НЕ

Номер строки	Входные переменные		Текущее состояние		Новое состояние			Адрес
	R	S
	3	2	1	0	1	0	Разряд
0	0	0	0	0	0	Ø	Таб.1
1	0	0	0	1	0	1	+1
2	0	0	1	0	1	0	+2
3	0	0	1	1	Ø	Ø	+3
4	0	1	0	0	1	0	+4
5	0	1	0	1	1	0	+5
6	0	1	1	0	1	0	+6
7	0	1	1	1	Ø	Ø	+7
8	1	0	0	0	0	1	+8
9	1	0	0	1	0	1	+9
10	1	0	1	0	0	1	+10
11	1	0	1	1	0	1	+11
12	1	1	0	0	0	0	+12
13	1	1	0	1	0	0	+13
14	1	1	1	0	0	0	+14
15	1	1	1	1	0	0	+15

Таблица переходов позволяет определить новое состояние устройства, таблица выходов формирует выходной сигнал. В данном случае таблица выходов совпадает со столбцами нового состояния таблицы переходов.

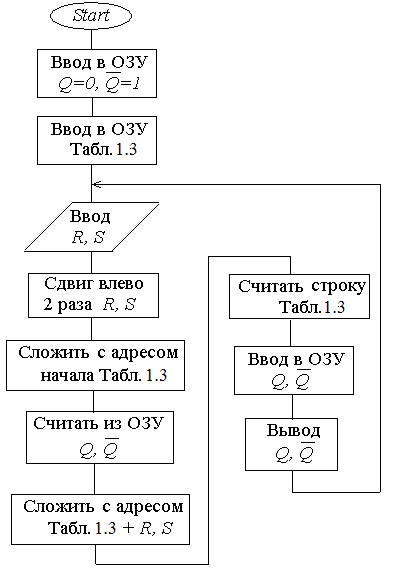
Рис. 1.12. Алгоритм интерпретирующей программы

RS – триггера в базисе ИЛИ-НЕ

Принцип построения алгоритма и программы сводится к следующим действиям:

– ввести в оперативную память первоначальные значения выходов триггера Q;

– в другую ячейку оперативной памяти необходимо ввести начальный адрес таблицы переходов. К этому адресу прибавить состояния выходов триггера;

– считать значения входных переменных, полученное число сдвинуть влево на два разряда и прибавить к адресу;

– считать новое состояние триггера, данные необходимо перенести в оперативную память.

На рис. 1.13 показаны схемы дуальных (инверсных) RS-триггеров. Эти триггеры переключаются в противоположное состояние нулевым потенциалом.

Рис. 1.13. Схемы RS-триггеров в базисе И-НЕ

Ниже приведены: карты Карно, функции алгебры логики, описывающие эти триггеры, таблица переходов и граф состояний триггеров.

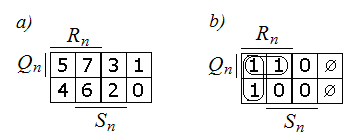
Рис. 1.14. Карты Карно RS-триггера в базисе И-НЕ

Функции алгебры логики, описывающие работу RS– триггера, в базисе И–НЕ:

(1.2)

Если R_n=S_n=0, на обоих выходах триггера будут единицы, что соответствует неопределенному состоянию триггера.

Таблица 1.4

Таблица состояний асинхронного RS-триггера в базисе И-НЕ

Набор	Входные переменные		Тек. Сост.	Нов. Сост.	Набор	Входные переменные		Тек. Сост.	Нов. Сост.
	Rn	Sn	Qn	Qn+1		Rn	Sn	Qn	Qn+1
0	0	0	0	Ø	4	1	0	0	1
1	0	0	1	Ø	5	1	0	1	(1)
2	0	1	0	(0)	6	1	1	0	(0)
3	0	1	1	0	7	1	1	1	(1)

Рис. 1.15. Граф состояний RS-триггера, построенного в базисе И-НЕ