3. Метод адресных переходов (табулирование функций)

Метод адресных переходов основан на табулировании функций --- замены функции таблицей из двух столбцов, первый из которых содержит все допустимые наборы значений входных переменных, а второй --- значение функции на соответствующем наборе. Для функций алгебры логики такая таблица называется таблицей истинности.

Алгоритм реализации метода следующий:

1. Составить таблицу истинности ФАЛ. Размер таблицы должен составлять 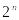, где 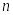— число входных переменных.

2. Задаться интерфейсом микропроцессорной системы. Этот шаг аналогичен шагу в предыдущем алгоритме, использующем метод непосредственного вычисления ФАЛ.

3. Записать последовательность мнемоник ассемблера, преобразующую набор входных переменных в адрес ячейки, содержащей значение функции на данном наборе.

4. Записать последовательность мнемоник ассемблера, возвращающую значение ФАЛ по заданному адресу.

5. Разместить тем или иным способом таблицу в памяти ОМЭВМ.

Достоинством метода является наименьшая вычислительная сложность среди трех методов, описываемых в настоящем пособии. Вычислительная сложность метода адресных переходов никак не связана с размером и сложностью моделируемой функции. Недостатком метода является расход памяти на таблицу истинности, который зависит как от числа входных переменных.

Размещать таблицу истинности в памяти ОМЭВМ можно несколькими способами. Двумя наиболее распространенными из них являются способы размещения в ОЗУ и в ПЗУ. В качестве примера будет использоваться способ размещения данных в ПЗУ, т.к. он более простой в реализации на архитектуре PIC. Способ размещения в ОЗУ описан в приложении В.

Преобразование набора входных величин в адрес производится на основе следующих соображений. Любой адрес в ОМЭВМ представляет собой двоичное число. Поэтому, если взять произвольную ячейку памяти и заменить значения её младших разрядов значениями входных переменных, получим смещение относительно начала таблицы. Если затем прибавить адрес нулевой ячейки таблицы к полученному смещению, то получим адрес ячейки в котором находится искомое значение функции.

Для способа хранения таблицы в ПЗУ это реализуется следующим образом:

movlw 1 ; Предположим, что входной набор дал

; смещение 1

fcall lookup_table

... ; <- здесь в регистре W находится

; значение функции на заданном наборе

lookup_table:

addwf pcl ; Прибавляем начальный адрес

; к смещению в регистре W

retlw 0 ; 0-я ячейка таблицы

retlw 0 ; 1-я ячейка таблицы

...

retlw 1 ; N-я ячейка таблицы

Подобную таблицу следует размещать как можно ближе к началу исходного текста --- для того, чтобы её начальный адрес получился как можно меньшим. Несоблюдение этого правила может привести к тому, что в результате вычисления адресного перехода регистр переполнится и переход будет осуществлен неверно. Например, пусть таблица расположена в ПЗУ по адресу 250 и содержит 64 ячейки. Допустим нам необходимо получить содержимое 20-й ячейки, имеющей адрес 270. Произойдет следующее

movlw 20

fcall lookup_table

... ; <- сюда программа не вернется

; вследствие потери управления

250: lookup_table:

250: addwf pcl ; pcl = 250;

; 250 + 20 = 14 (!)

251: retlw 0 ; 1-я ячейка таблицы

252: retlw 0 ; 2-я ячейка таблицы

...

270: retlw 1 ; 20-я ячейка таблицы

и переход будет осуществлен на адрес 14, а не на 270.

В качестве примера, реализуем ФАЛ

методом адресных переходов. ФАЛ будет иметь следующую таблицу истинности

a	0	0	0	0	1	1	1	1
b	0	0	1	1	0	0	1	1
c	0	1	0	1	0	1	0	1
f	0	0	0	1	1	1	1	1

Интерфейс аналогичен описанному в разделе 3.1, за исключением отсутствия входной переменной d.

#define IN_A PORTB, 0

#define IN_B PORTB, 1

#define IN_C PORTB, 2

#define IN_C 2

#define OUT_F PORTC, 0

Преобразование входного набора в смещение производится следующим образом:

OFFSET: equ H'20'

RESULT: equ H'21'

movlw 0

movwf OFFSET

btfsc IN_A

bsf OFFSET, 2

btfsc IN_B

bsf OFFSET, 1

btfsc IN_C

bsf OFFSET, 0

Получение значения ФАЛ по заданному смещению и формат таблицы истинности аналогичны вышеописанному.

movf OFFSET

fcall lookup_table

lookup_table:

addwf pcl

retlw 0

retlw 0

retlw 0

retlw 1

retlw 1

retlw 1

retlw 1

retlw 1

Последним шагом будет размещение после инструкции fcall кода записи значения функции в выходную переменную и перехода на начало алгоритма.

movwf RESULT

decfsz RESULT

goto OUT_0

goto OUT_1

OUT_0:

bcf OUT_F

goto main

OUT_1:

bsf OUT_F

goto main

Полный исходный текст примера приведен в приложении А.3.