5. Пример разработки имитационной модели триггерного устройства

Порядок создания имитационной модели рассмотрим на примере рис. 1.65, на котором изображён тактируемый потенциальный Е–триггер. Особенностью этого триггера является то, при одновременной подаче на все входы R, S и C единиц состояние триггера не изменяется.

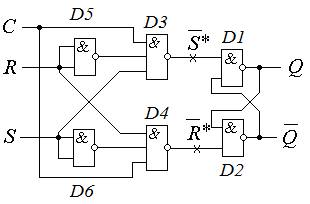
Рис. 1.65. Тактируемый потенциальный Е-триггер

Как указывалось во введении, задачу разработки имитационной модели можно решить различными путями, но наиболее распространенными являются три: непосредственное решение уравнений, описывающих работу устройства, использование графа состояний этого устройства и применение таблицы переходов рассматриваемого устройства из одного состояния в другое, и поиск нужной строки этой таблицы.

1. Непосредственное решение уравнений, описывающих работу триггерной установки

Уравнения функции алгебры логики, описывающие работу Е-триггера, выглядят следующим образом:

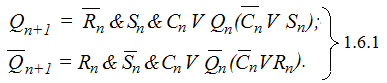
Эту же задачу можно решить и другим способом, вычислив сначала значения внутренних переменных R* и S*, а затем, определив состояние триггера, воспользовавшись уравнениями 1.6.2 и 1.6.3, которые будут универсальными для любого триггера.

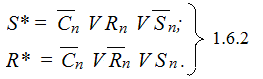
Поскольку R* и S* не могут одновременно равняться нулю во втором случае инверсное значение состояния триггера можно не вычислять.

Алгоритмы непосредственных решений функций, описывающих работу триггера, представлены на рис.1.66.

Методы решения указанных на рис. 1.66 уравнений зависят от того, на каком алгоритмическом языке ведётся программирование. При применении алгоритмического языка нижнего уровня (Ассемблера) обычно используют один из трёх методов: непосредственное решение ФАЛ, метод бинарных функций и метод адресных переходов. Эти методы достаточно подробно изложены в подразделе 1.1 и в [1, 2].

Примечания.

– Приведенные в алгоритмах ФАЛ могут быть решены любым из рассмотренных выше методом.

– Передача выходного слова может не предусматриваться.

– Достоверные данные можно получить при двукратном решении задачи (без изменения значений входных переменных).

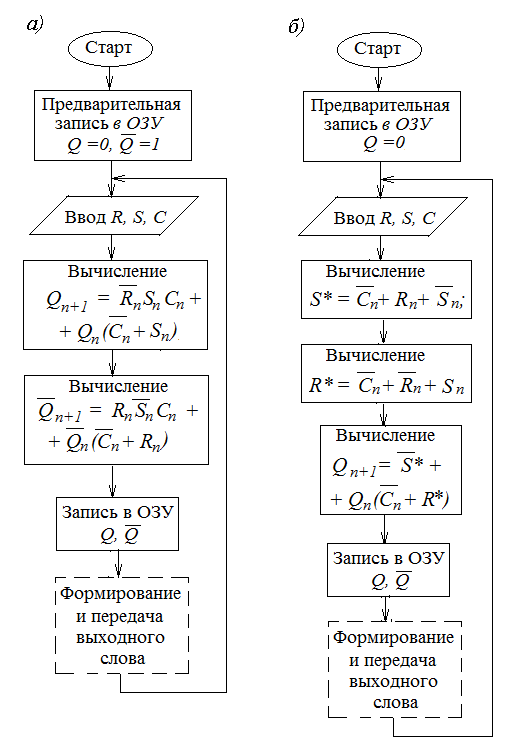
Рис. 1.66. Алгоритмы непосредственных решений уравнений

2. Использование графа состояний триггерного устройства для разработки алгоритма

Граф состояний триггерного устройства, изображённого на рис. 1.65, приведён на рис. 1.67.

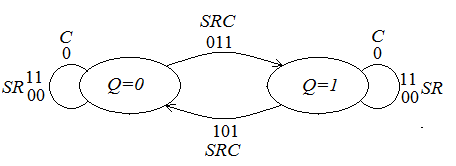
Рис. 1.67. Граф состояний Е-триггера

Для каждого устойчивого состояния создаётся блок программы, который включает в себя:

– передачу выходного слова (если это необходимо);

– обновление записи в ячейке ОЗУ «Текущее состояние»;

– считывание внешних переменных;

– решение уравнения условий перехода в следующее состояние. Если условие перехода выполняется, осуществляется переход к следующему блоку программы, при невыполнении условия перехода – к началу данного блока программы.

В рассматриваемом случае условиями переходов будут внутренние переменные S* и R*. Алгоритм приведён на рис. 1.68.

Следует отметить, что в этом случае программа получается проще и не требует двукратного её выполнения.

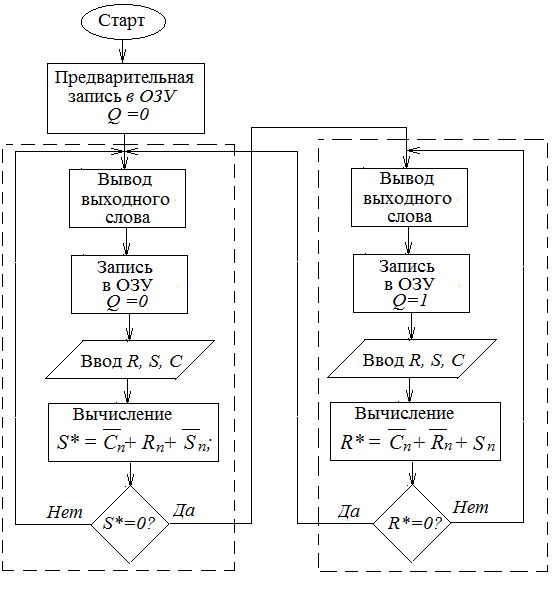
Рис. 1.68. Алгоритм, использующий граф состояний

триггерного устройства

3. Применение таблицы переходов для решения поставленной задачи

Метод предусматривает предварительное решение функций алгебры логики и заполнение таблицы переходов, которая помещается в ОЗУ. В задачу программы входит поиск строки этой таблицы, где записано новое состояние моделируемого объекта (в нашем случае – триггера). Программа получается весьма простой и универсальной. К недостаткам можно отнести повышенный расход оперативной памяти для хранения таблицы переходов.

Таблица 1.10

Таблица переходов E-триггера.

Текущее состояние	Входные переменные			Новое состояние	Адрес ОЗУ
Qn	Sn	Rn	Cn	Qn+1
0	0	0	0	0	Table
0	0	0	1	0	+1
0	0	1	0	0	+2
0	0	1	1	0	+3
0	1	0	0	0	+4
0	1	0	1	1	+5
0	1	1	0	0	+6
0	1	1	1	0	+7
1	0	0	0	1	+8
1	0	0	1	1	+9
1	0	1	0	1	+a
1	0	1	1	0	+b
1	1	0	0	1	+c
1	1	0	1	1	+d
1	1	1	0	1	+e
1	1	1	1	1	+f

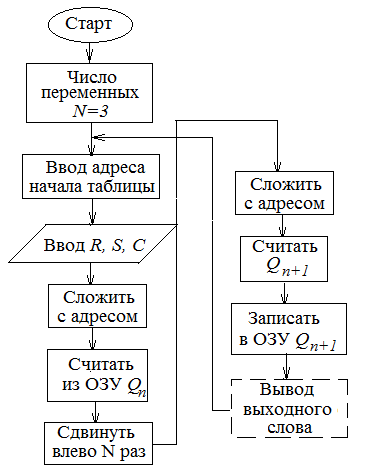
Рис. 1.69. Алгоритм решения задачи с использованием

таблицы переходов