
- •«Мурманский государственный технический университет»
- •Предел и непрерывность функций одной переменной
- •«Математический анализ»
- •Предел последовательности
- •Примеры исследования последовательностей с точки зрения существования их предела
- •Определение сходящейся или расходящейся, бесконечно большой и бесконечно малой последовательности
- •Упражнения для самостоятельной работы
- •Основные свойства предела последовательности. Ограниченные последовательности
- •1.Единственность предела
- •2.Предел стационарной последовательности
- •3.Переход к пределу в равенстве
- •4.Переход к пределу в неравенствах
- •5.Теорема о зажатой последовательности
- •6.Связь сходящейся последовательности с её пределом и бесконечно малой последовательностью
- •7.Ограниченность последовательности, связь с пределом
- •8.Упражнения для самостоятельной работы
- •Основные теоремы о бесконечно малых, бесконечно больших и сходящихся последовательностях
- •Основные теоремы о бесконечно малых последовательностях
- •Основные теоремы о бесконечно больших последовательностях
- •Теоремы о сходящихся последовательностях
- •Примеры практического вычисления пределов. Понятие о неопределенностях
- •Упражнения для самостоятельной работы
- •Предел монотонной и ограниченной оследовательности. Определение числа e
- •1.Определение монотонной последовательности
- •2.Теорема Вейерштрасса о пределе монотонной последовательности
- •3.Примеры доказательства существования предела монотонной ограниченной последовательности
- •4.Определение числа
- •5.Упражнения для самостоятельного решения
- •Подпоследовательности. Частичные пределы последовательности. Критерий Коши сходящейся последовательности
- •6.Определение подпоследовательности
- •7.Связь предела последовательности с пределами ее подпоследовательностей
- •8.Принцип компактности отрезка (теорема Больцано - Коши)
- •9.Критерий Коши существования конечного предела последовательности
- •10.Упражнения для самостоятельной работы
Основные теоремы о бесконечно больших последовательностях
-
Теорема о сумме двух бесконечно больших последовательностей, имеющих одинаковый знак
Если две последовательности и являются бесконечно большими при и их члены при этом имеют одинаковый знак, то их сумма также является бесконечно большой последовательностью при .
По определению бесконечно большой последовательности имеем:

Тогда при
,
где
![]() верно неравенство
верно неравенство
![]() .
.
Теперь используем известное свойство
модуля:
![]() ,
причем
,
причем
![]() только тогда, когда
и
имеют одинаковые знаки. По условию
теоремы числа
только тогда, когда
и
имеют одинаковые знаки. По условию
теоремы числа
![]() и
и
![]() имеют одинаковые знаки, поэтому
имеют одинаковые знаки, поэтому
![]() .
.
Следовательно, при
![]() верно неравенство
верно неравенство
![]() ,
где
- произвольное
малое число. Это означает, что
,
где
- произвольное
малое число. Это означает, что
![]() ,
то есть последовательность
,
то есть последовательность
![]() является бесконечно большой при
.
является бесконечно большой при
.
-
Теорема о сумме бесконечно большой и ограниченной последовательностей
Если последовательность является бесконечно большой при и последовательность является ограниченной, то их сумма является бесконечно большой последовательностью при .
Запишем определения ограниченной последовательности и бесконечно большой последовательности:
1)
![]() – ограниченная
– ограниченная
![]() ;
;
очевидно, что из неравенства
![]() следует неравенство
следует неравенство
![]() ;
;
2)
– б. б.
![]() ,
,
где – сколь угодно малое число;
если обозначить
![]() ,
то определение б. б. можно записать
несколько иначе:
,
то определение б. б. можно записать
несколько иначе:
![]() ,
,
где M – сколь угодно большое число.
Теперь рассмотрим
![]() ,
используя при этом свойство модуля
,
используя при этом свойство модуля
![]() :
:
![]() .
.
Таким образом показано, что для любого
числа
![]() ,
сколь большим бы его ни брать, существует
номер
,
сколь большим бы его ни брать, существует
номер
![]() такой, что при
выполняется неравенство
такой, что при
выполняется неравенство
![]() .
По определению бесконечного предела
это означает, что
.
По определению бесконечного предела
это означает, что
![]() ,
то есть последовательность
,
то есть последовательность
![]() б.
б при
б.
б при
-
Теорема о произведении бесконечно больших последовательностей
Если две последователности и
 являются бесконечно большими при
,
то их произведение
являются бесконечно большими при
,
то их произведение
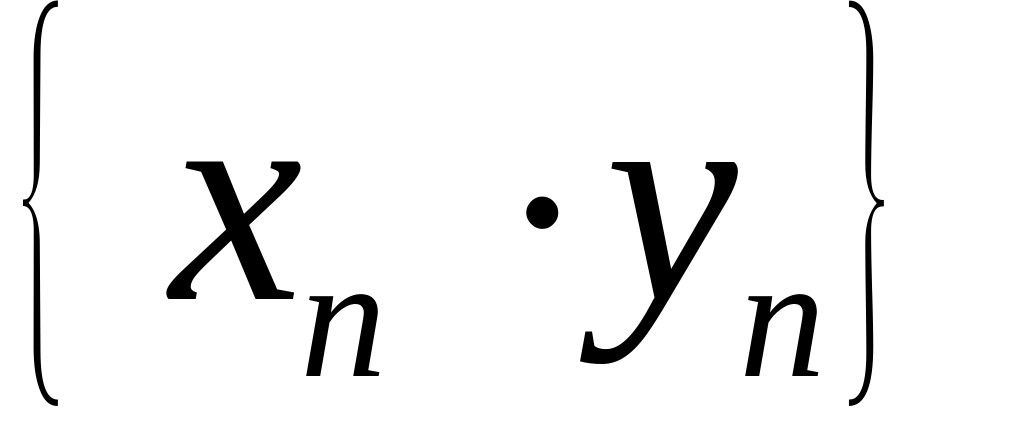 также есть бесконечно большая
последовательность при
.
также есть бесконечно большая
последовательность при
.

![]() ;
;
таким образом показано, что
![]()
![]() .
.
-
Теорема о связи бесконечно большой с бесконечно малой последовательностью
Если
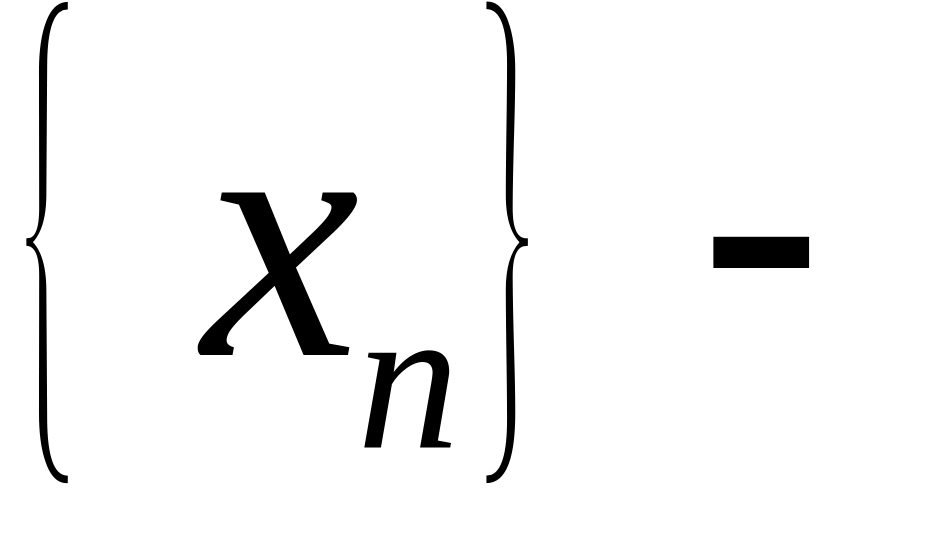 б.б.
при
и
б.б.
при
и
 ,
то последовательность
,
то последовательность
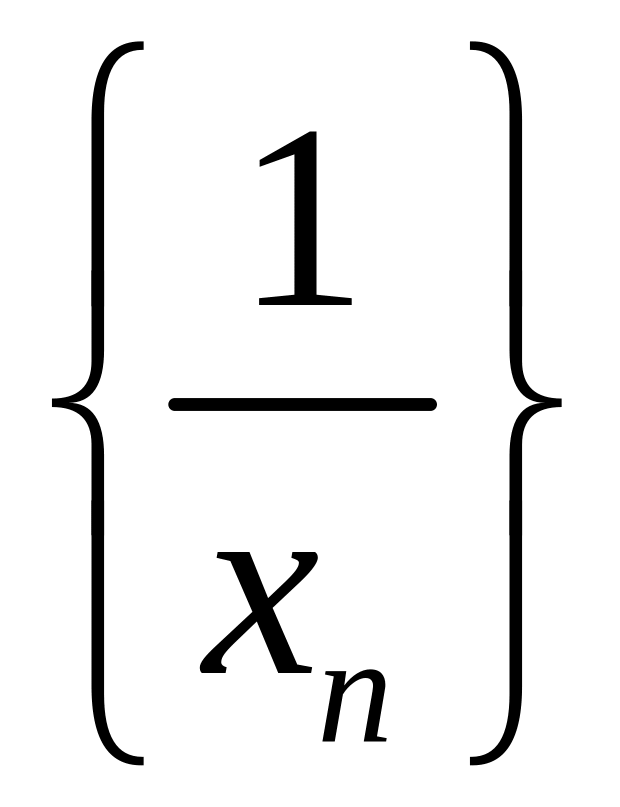 является бесконечно малой при
.
является бесконечно малой при
.
![]()
![]()
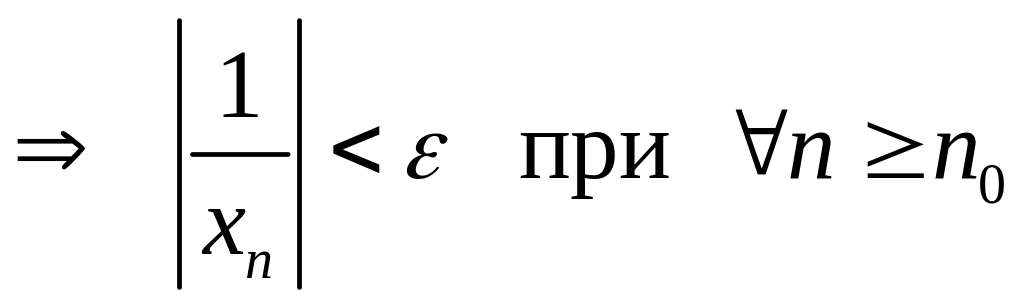 для любого числа
,
сколь малым бы оно ни было,
для любого числа
,
сколь малым бы оно ни было,
 является б.м. при
.
является б.м. при
.
-
Теорема о произведении бесконечно большой на ограниченную последовательность
Если последовательность бесконечно большая при
 ,
последовательность
,
последовательность
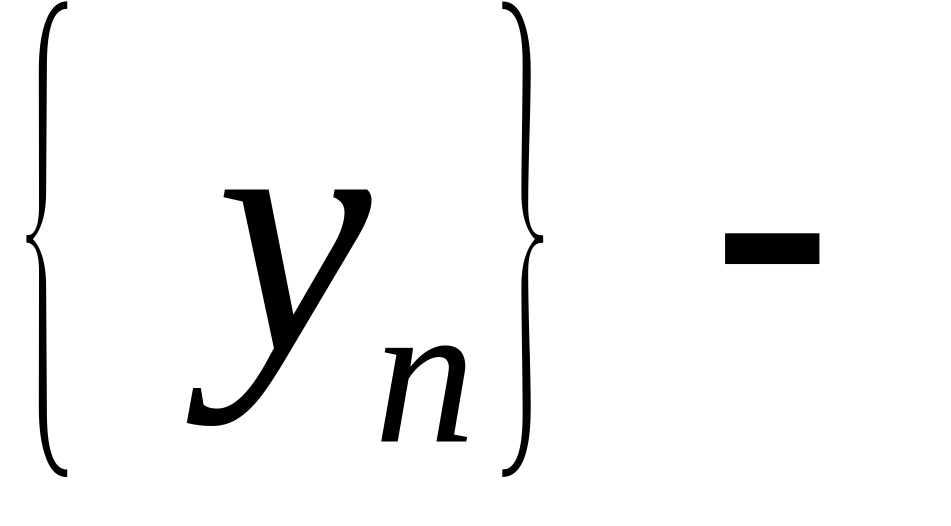 ограниченная,
но не является бесконечно малой, и
все её члены отличны от нуля (хотя бы
начиная с некоторого номера
),
то произведение этих последовательностей
есть бесконечно бальшая последовательность
при
.
ограниченная,
но не является бесконечно малой, и
все её члены отличны от нуля (хотя бы
начиная с некоторого номера
),
то произведение этих последовательностей
есть бесконечно бальшая последовательность
при
.
Поработаем с ограниченной
последовательностью
:
учитывая, что она не является бесконечно
малой и что все её члены отличны от нуля
(хотя бы начиная с некоторого номера
![]() ),
при
можно зафиксировать ограниченность
членов этой последовательности по
модулю:
),
при
можно зафиксировать ограниченность
членов этой последовательности по
модулю:
![]() ,
где a и b
– положительные числа; перейдем к
неравенству обратных величин и получим,
что
,
где a и b
– положительные числа; перейдем к
неравенству обратных величин и получим,
что
![]() ,
то есть последовательность
,
то есть последовательность
![]() также является ограниченной.
также является ограниченной.
Теперь поработаем с бесконечно большой
последовательностью
:
так как
![]() ,
то последовательность из обратных
величин
,
то последовательность из обратных
величин
![]() может быть образована и является
бесконечно малой (по теореме о связи
бесконечно большой с бесконечно малой
последовательностью); очевидно, что
также является бесконечно малой и
последовательность из модулей
может быть образована и является
бесконечно малой (по теореме о связи
бесконечно большой с бесконечно малой
последовательностью); очевидно, что
также является бесконечно малой и
последовательность из модулей
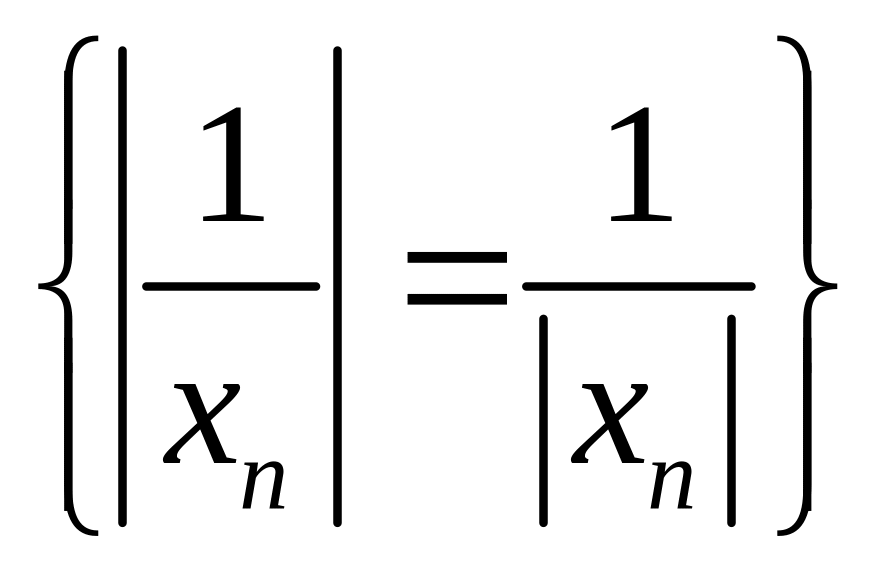 .
.
Рассмотрим
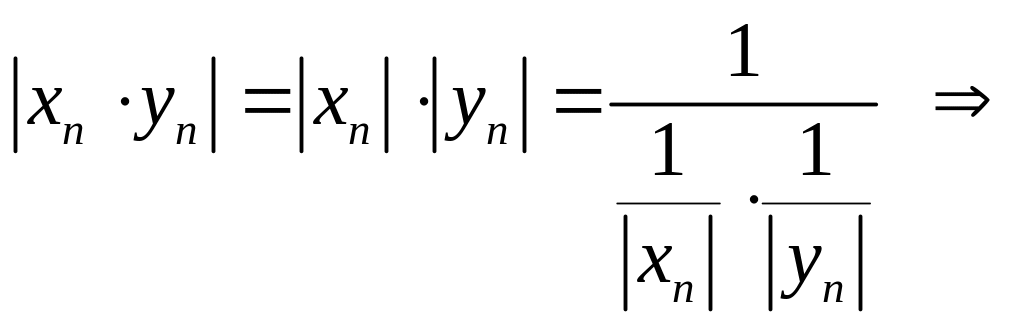
в знаменателе имеем произведение
бесконечно малой последовательности
![]() на ограниченную последовательность
на ограниченную последовательность
![]() ;
по теоремам о бесконечно малых величины
;
по теоремам о бесконечно малых величины
![]() образуют бескнечно малую последовательность,
тогда обратные им величины
образуют бескнечно малую последовательность,
тогда обратные им величины
![]() образуют бесконечно большую
посоледовательность; следовательно,
последовательность
образуют бесконечно большую
посоледовательность; следовательно,
последовательность
![]() является б. б. при
.
является б. б. при
.
