
- •«Мурманский государственный технический университет»
- •Предел и непрерывность функций одной переменной
- •«Математический анализ»
- •Предел последовательности
- •Примеры исследования последовательностей с точки зрения существования их предела
- •Определение сходящейся или расходящейся, бесконечно большой и бесконечно малой последовательности
- •Упражнения для самостоятельной работы
- •Основные свойства предела последовательности. Ограниченные последовательности
- •1.Единственность предела
- •2.Предел стационарной последовательности
- •3.Переход к пределу в равенстве
- •4.Переход к пределу в неравенствах
- •5.Теорема о зажатой последовательности
- •6.Связь сходящейся последовательности с её пределом и бесконечно малой последовательностью
- •7.Ограниченность последовательности, связь с пределом
- •8.Упражнения для самостоятельной работы
- •Основные теоремы о бесконечно малых, бесконечно больших и сходящихся последовательностях
- •Основные теоремы о бесконечно малых последовательностях
- •Основные теоремы о бесконечно больших последовательностях
- •Теоремы о сходящихся последовательностях
- •Примеры практического вычисления пределов. Понятие о неопределенностях
- •Упражнения для самостоятельной работы
- •Предел монотонной и ограниченной оследовательности. Определение числа e
- •1.Определение монотонной последовательности
- •2.Теорема Вейерштрасса о пределе монотонной последовательности
- •3.Примеры доказательства существования предела монотонной ограниченной последовательности
- •4.Определение числа
- •5.Упражнения для самостоятельного решения
- •Подпоследовательности. Частичные пределы последовательности. Критерий Коши сходящейся последовательности
- •6.Определение подпоследовательности
- •7.Связь предела последовательности с пределами ее подпоследовательностей
- •8.Принцип компактности отрезка (теорема Больцано - Коши)
- •9.Критерий Коши существования конечного предела последовательности
- •10.Упражнения для самостоятельной работы
Упражнения для самостоятельной работы
} 1. Для нескольких последовательностей известны формулы общего члена:
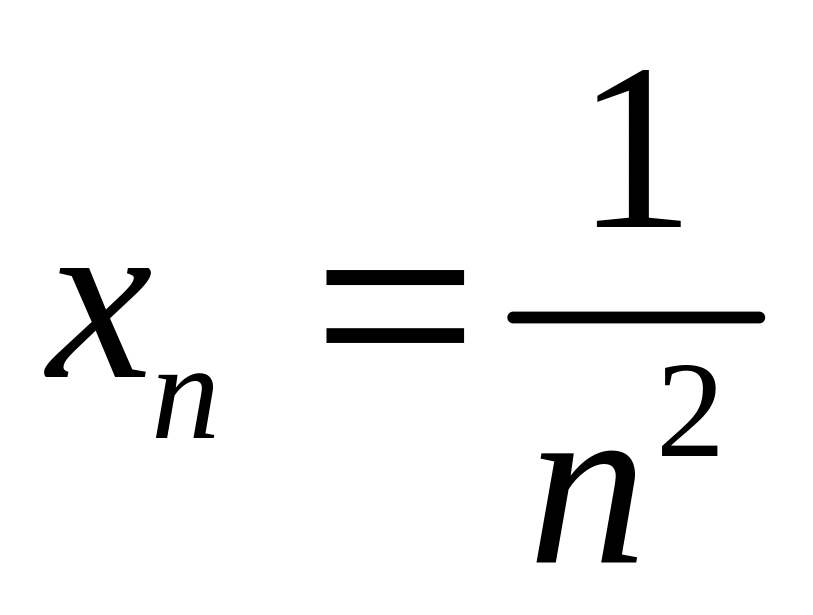 ;
2)
;
2)
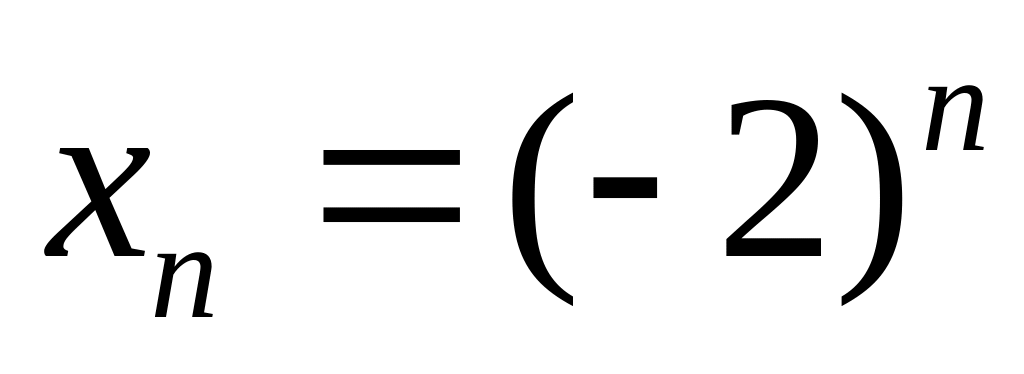 ;
3)
;
3)
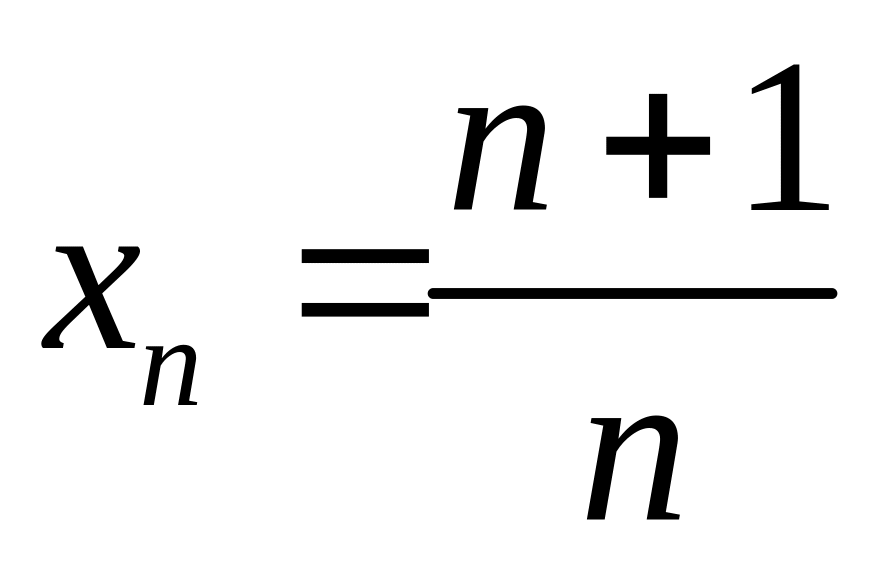 ;
4)
;
4)
 ;
5)
;
5)
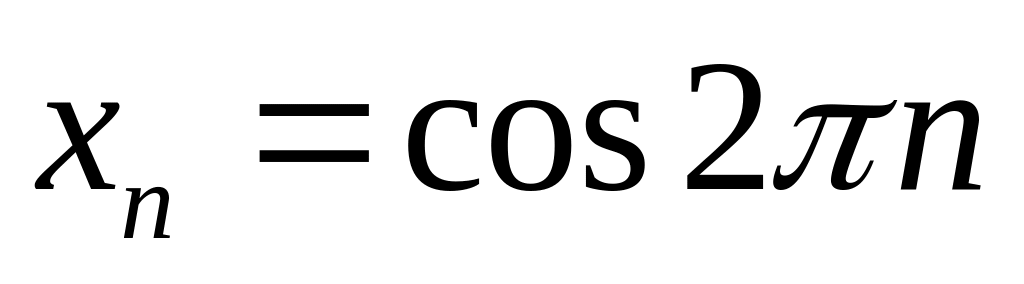 ;
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
9)
;
9)
![]() ;
10)
;
10)
![]() .
.
Для каждой из этих последовательностей
вычислите несколько первых членов и
по расположению чисел
на координатной оси сделайте вывод
о
![]() .
.
2. Среди последовательностей предыдущего задания укажите номера сходящихся, расходящихся, бесконечно больших и бесконечно малых последовательностей.
3. Докажите строго по определению предела, что :
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
Ответы к упражнениям для самостоятельной работы
1. 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() .
.
2. Номера сходящихся последовательностей: 1), 3), 5), 6), 9), 10);
расходящихся последовательностей: 2), 4), 7), 8);
бесконечно больших последовательностей: 2), 8);
бесконечно малых последовательностей: 1), 6), 9), 10).
Основные свойства предела последовательности. Ограниченные последовательности
1.Единственность предела
-
Теорема о единственности предела
Если существует предел последовательности , то этот предел является единственным
Проведем доказательство от противного.
Предположим, что последовательность
имеет два различных предела:
![]() и
и
![]() .
.
У двух различных точек а и b
координатной прямой (возможно,расширенной)
всегда можно указать непересекающиеся
![]() - окрестности:
- окрестности:
![]() (это одно из свойств окрестностей).
(это одно из свойств окрестностей).
По определению предела имеем:

Следовательно, при![]() ,
где
,
где
![]() ,
все
входят в обе окрестности
,
все
входят в обе окрестности
![]() и
и
![]() ,
что невозможно, так как окрестности не
пересекаются. Получившееся противоречие
говорит о том, что предположение о двух
различных пределах одной и той же
последовательности является неверным.
Следовательно, верно противоположное:
последовательность может иметь только
один предел, ч.т.д.
,
что невозможно, так как окрестности не
пересекаются. Получившееся противоречие
говорит о том, что предположение о двух
различных пределах одной и той же
последовательности является неверным.
Следовательно, верно противоположное:
последовательность может иметь только
один предел, ч.т.д.
Иллюстрация к приведенному доказательству в случае, когда оба предела a и b являются конечными, показана на рис. 14.
-

Рис. 14
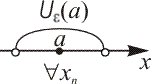
Рис. 15
2.Предел стационарной последовательности
-
Теорема о пределе стационарной последовательности
Если все члены стационарной последовательности равны числу a, то существует предел этой последовательности, равный числу a:
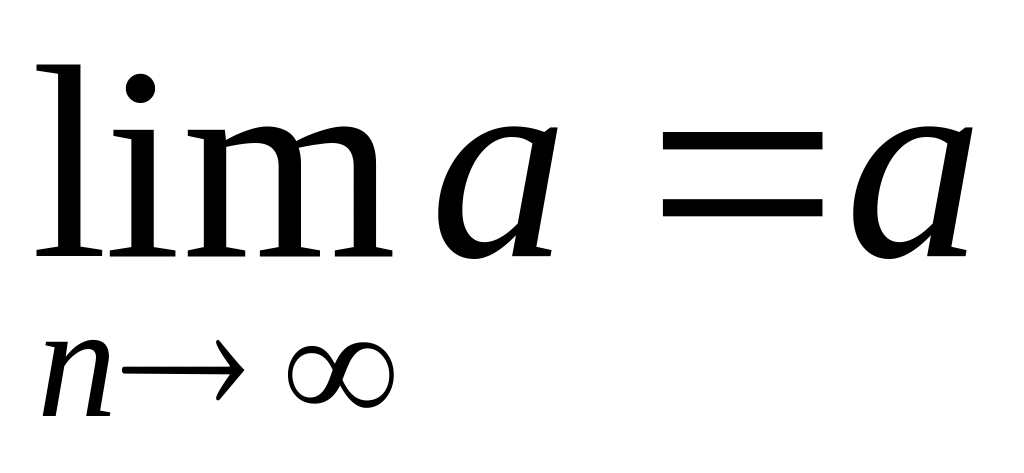 .
.
Пусть
![]() ,
тогда
,
тогда
![]() будет
будет
![]() при
при
![]() ;
;
по определению конечного предела заключаем, что , т.е. предел постоянной последовательности существует и равен этой постоянной, (рис. 15).
3.Переход к пределу в равенстве
-
Теорема о переходе к пределу в равенстве
Если члены двух последовательностей и
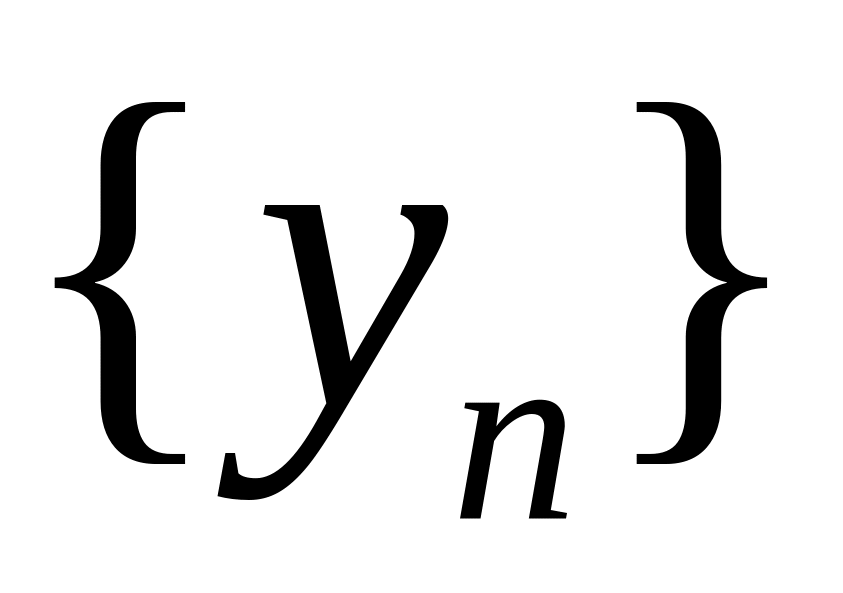 совпадают (начиная хотя бы с некоторого
номера
)
и обе эти последовательности имеют
пределы, то их пределы равны:
совпадают (начиная хотя бы с некоторого
номера
)
и обе эти последовательности имеют
пределы, то их пределы равны:
если
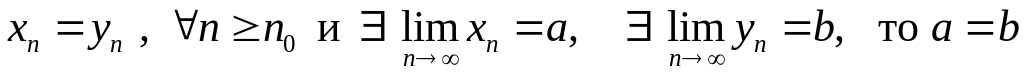 .
.
![]() .
Так как при всех
.
Так как при всех
![]() верно равенство
верно равенство
![]() ,
то при
,
то при
![]() будет верно, что
будет верно, что
![]() ,
где
,
где
![]() – это произвольное малое число. Отсюда
на основании определения предела
заключаем, что
– это произвольное малое число. Отсюда
на основании определения предела
заключаем, что
![]() .
Так как последовательность может иметь
только один предел, то
.
Так как последовательность может иметь
только один предел, то
![]() ,
ч.т.д.
,
ч.т.д.
Иллюстрация к свойству приведена на рис. 16:

Рис. 16
Другими словами доказанное свойство можно сформулировать так:
в равенстве
![]() можно переходить к пределу:
можно переходить к пределу:
![]()
(при условии, что предел правой и левой частей существуют).
