Федеральное агентство по рыболовству

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ бЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОРАЗОВАНИЯ

«Мурманский государственный технический университет»

Кафедра Высшей математики и программного обеспечения ЭВМ

Предел и непрерывность функций одной переменной

Электронный конспект лекций

по дисциплине

«Математический анализ»

для бакалавров 1 курса направления 230100 «Информатика и вычислительная техника»

Автор ЭКЛ: Кацуба Валентина Сергеевна – к.ф.-м.н., доцент,

Мурманск

2025 г.

Оглавление

Введение

Тема I. Предел последовательности

1. Предел последовательности и его основные свойства

Числовая последовательность

Определение числовой последовательности

Числовой последовательностью 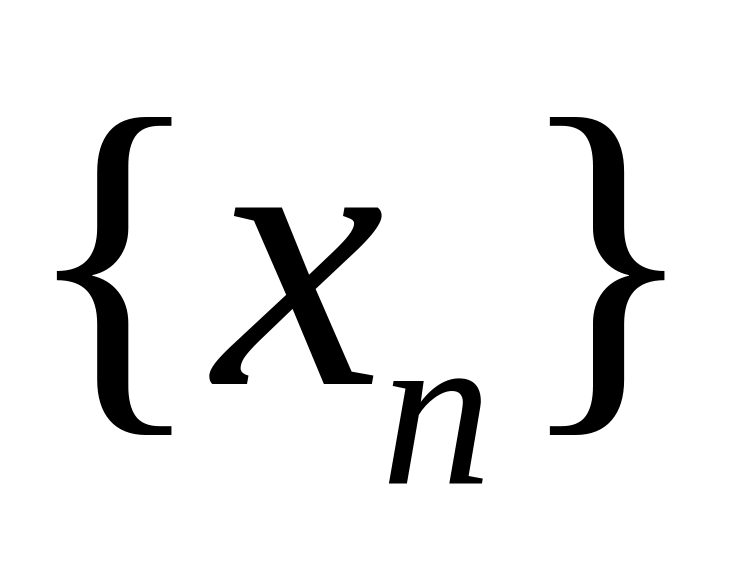  элементов некоторого множества  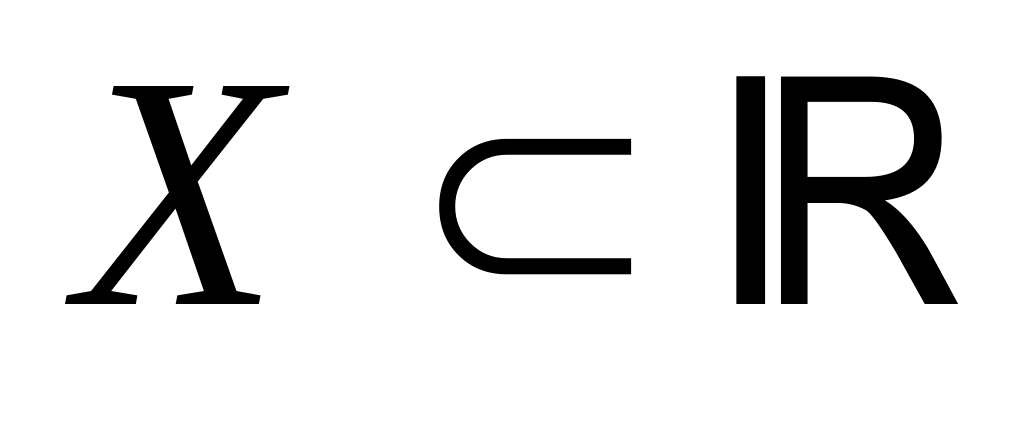называется отображение множества натуральных чисел на это множество : .

Из определения следует, что числовая последовательность есть функция натурального аргумента ; множество её определения является бесконечным и счетным; множество значений функции может быть бесконечным счетным или конечным.

Числа называются членами последовательности:

 - первый   член, -  второй     член, …, -  - й   член    или   общий член последовательности.

Будем далее называть числовую последовательность просто последовательностью.

Пример (числовые последовательности)

1)

2)

3) ;

4) , т.е. .

В случае, когда множество состоит из одного элемента (т.е. все члены последовательности   одинаковы),      называется    стационарной последовательностью.

Геометрическое изображение членов последовательности

Так как числовая последовательность  есть функция: , , то для неё возможно изображение графиком, например, в декартовой системе координат (рис. 1).

Рис. 1

График представляет собой дискретное множество точек плоскости и является избыточным изображением в том смысле, что значения аргумента для любой последовательности  всегда одинаковы, а интерес представляют только поведение значений функции . Поэтому проще изображать последовательности как множество точек на одной координатной оси (рис. 2).

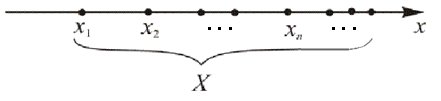
Рис. 2

Предел последовательности

Определение предела последовательности

Конечная или бесконечно удаленная точка а координатной прямой называется пределом числовой последовательности , если какова бы ни была окрестность точки а, она содержит все члены этой последовательности, начиная с некоторого номера .

Обозначения: или при или .

Краткая запись определения предела:

(1)

Геометрическая иллюстрация и формальное описание конечного предела последовательности

1. Если , то есть а – это конечная точка координатной прямой, то проиллюстрировать определение предела последовательности можно так, как на рис 3.

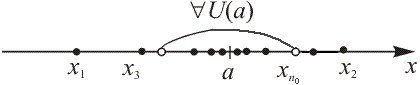
Рис. 3

При этом важно заметить следующие детали определения:

1) окрестность назначается произвольно; вне любой окрестности точки а может находиться лишь конечное количество членов последовательности , но внутри этой   же окрестности всегда находится их бесконечное количество — все , начиная с   некоторого номера ;

 2)  все числа стремятся (приближаются) к числу а в том смысле, что могут отличаться от него сколь угодно мало или, что то же, числа подходят к числу а сколь угодно близко;

 3)  приближение чисел к числу а возможно как с обеих сторон, так и только с одной стороны: слева или справа;

 4)  не исключается, что значения некоторых совпадают с числом а.

Если окрестность точки а описать как - окрестность, то нетрудно составить и проиллюстрировать формальное описание конечного предела последовательности (рис.4).

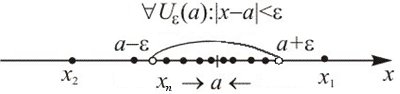
Рис. 4

(2)

Записанное определение (2) прочитывается следующим образом:

число а называется пределом числовой последовательности  , если для любого положительного числа , сколь малым бы оно ни было, можно указать номер , зависящий от , такой что выполняется неравенство для всех номеров n, начиная с номера .

Кратко смысл этого определения можно сформулировать так:

если , то это означает, что члены последовательности становятся сколь угодно близкими к числу , если брать номера достаточно большими.

Геометрическая иллюстрация и формальное описание предела последовательности, равного

2.  Если , то иллюстрация к определению в соответствии с формальной записью (1) имеет вид, приведенный на рис. 5.

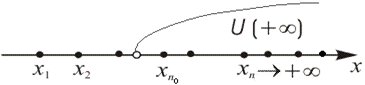
Рис. 5

При этом также замечаем, что вне любой окрестности может находиться лишь конечное число точек , внутри этой окрестности всегда находится бесконечное количество точек . Так как окрестность может назначаться любая, то числа должны увеличиваться с возрастанием номера и становиться сколь угодно большими.

Если окрестность точки описать как - окрестность: , то получится формальное описание предела, равного , и его иллюстрация (рис. 6):

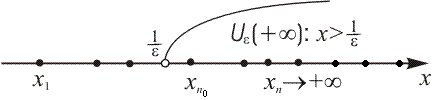
Рис. 6

   (3)

Формулируем краткий смысл этого определения:

если , то это означает, что члены последовательности становятся сколь угодно большими положительными, если брать номера достаточно большими.

Геометрическая иллюстрация и формальное описание предела последовательности, равного

3. Если   , то (рис.7)

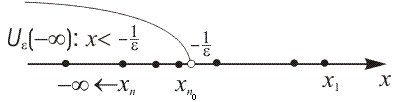
Рис.7

(4)

Краткое описание этого определения:

если , то это означает, что члены последовательности становятся сколь угодно большими по модулю, но отрицательными, если брать номера достаточно большими.}

Геометрическая иллюстрация и формальное описание предела последовательности, равного

4. Если   , то (рис. 8)

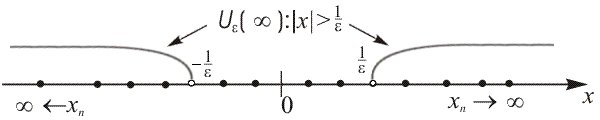
Рис.8

(5)

Краткий смысл этого определения:

если , то это означает, что члены последовательности становятся сколь угодно большими по модулю, если брать номера достаточно большими.