2.6. Прямоугольный декартов базис

Р ассмотрим прямоугольную систему координат в пространстве Е₃, образованную тремя взаимно перпендикулярными осями с общим началом в точке О (рис. 2.17). Одну из осей называют осью абсцисс и обозначают Ох, вторую – осью ординат и обозначают Оу, третью – осью аппликат и обозначают Оz. На каждой из осей выберем единичный вектор, направление которого совпадает с положительным направлением оси:

, , ; .

Эти векторы называются ортами. Так как орты некомпланарны, то они образуют базис, который называется декартовым ортогональным базисом.

Рассмотрим вектор в пространстве Е₃. Перенесём его параллельно самому себе в точку О (рис. 2.18).

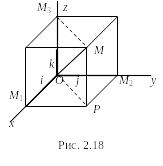
Получим – радиус-вектор точки М. Проведём , , , где М₁ – проекция точки М на ось Ох, М₂ – проекция точки М на ось Оу, М₃ – проекция точки М на ось Оz. Обозначим отрезки: , , ; ОР – диагональ прямоугольника . По определению операции сложения векторов , или . В прямоугольнике ОМ – диагональ, . Итак, , или , где числа – проекции вектора на координатные оси.

Найдём длину вектора как длину диагонали параллелепипеда (рис. 2.18):

,

или

. (2.4)

Модуль вектора равен корню квадратному из суммы квадратов его проекций на оси координат.

Пусть вектор имеет начальную точку и конечную . Найдём его длину.

Из определения проекции вектора на ось

, , ,

т. е. , , и по формуле (2.4) длина вектора или расстояние между точками А и В:

. (2.5)

На плоскости имеем две оси Ох и Оу с ортами i и j, следовательно, .

Для точек А(х₁, у₁), В(х₂, у₂), являющихся соответственно началом и концом вектора , формулы примут вид:

или

Пусть даны два вектора

тогда:

 два вектора равны, если равны их одноимённые проекции

 чтобы умножить вектор на число, достаточно умножить каждую его проекцию на это число:

,

где  = const;

 чтобы найти сумму (разность) двух векторов, надо сложить (вычесть) их одноимённые проекции:

.

 векторы и коллинеарны, если их соответствующие координаты пропорциональны:

.

Пример. Даны точки А(5, 0) и В(2, 4) на плоскости. Найти длину вектора .

Решение.

Найдём координаты вектора :

= {2 – 5, 4 – 0} = {–3, 4},

тогда

Направляющие косинусы вектора

Направление вектора в пространстве определяется углами ,  и  между вектором и положительным направлением соответствующих осей координат ОХ, ОУ, ОZ; cos , cos  и cos  называются направляющими косинусами вектора.

Возьмём вектор , где – проекции вектора на оси. Проекции вектора на оси:

, .

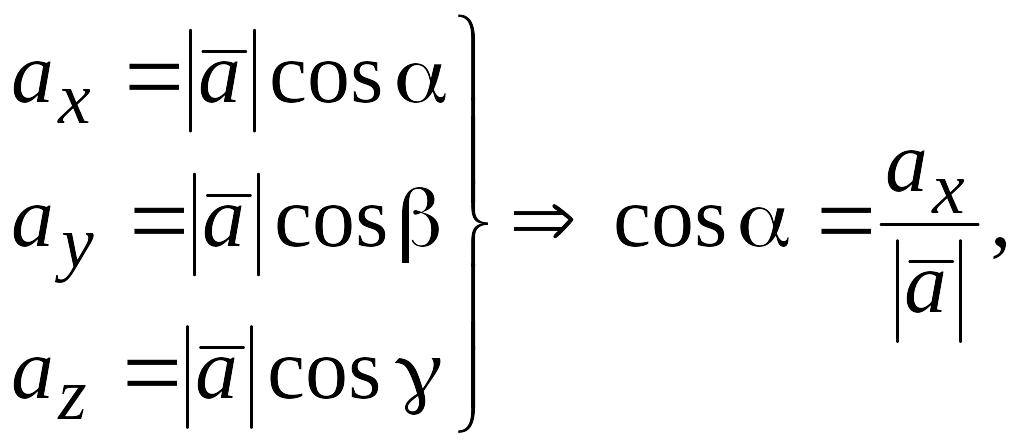
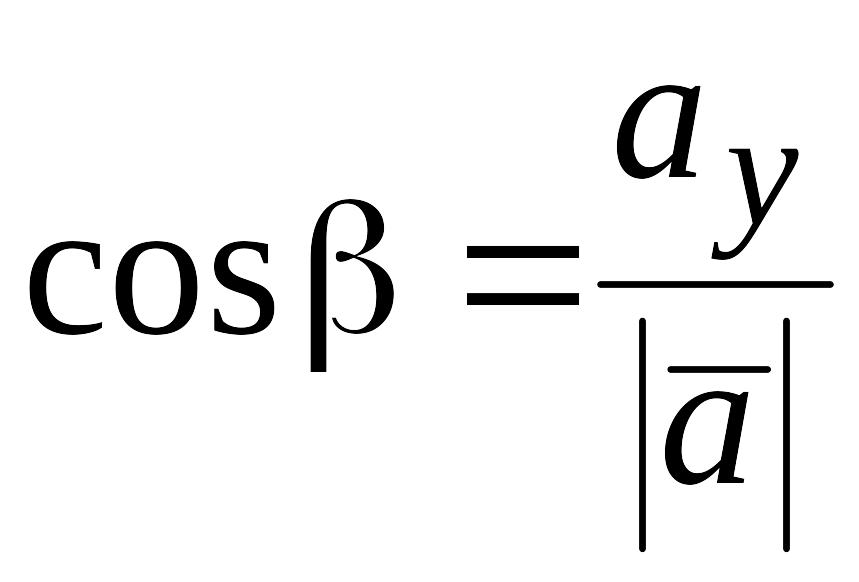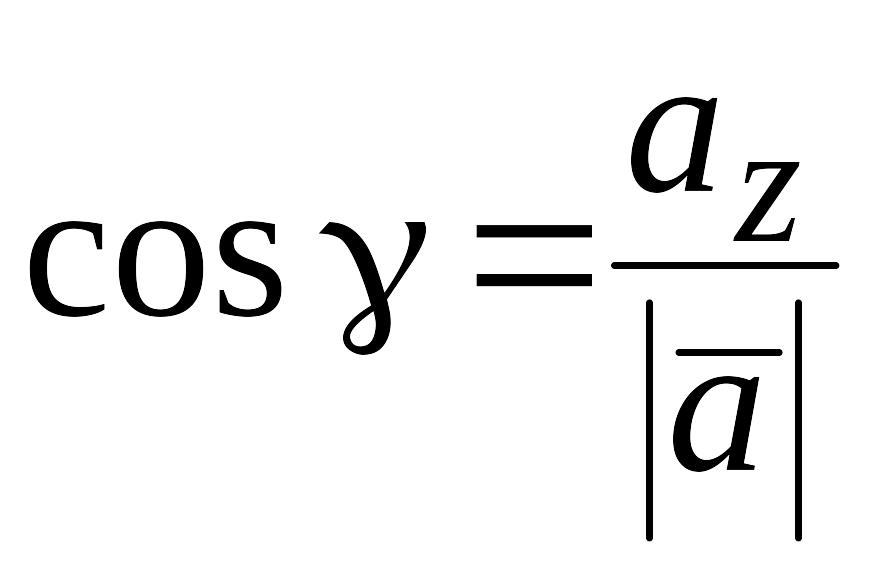Найдём длину вектора , откуда

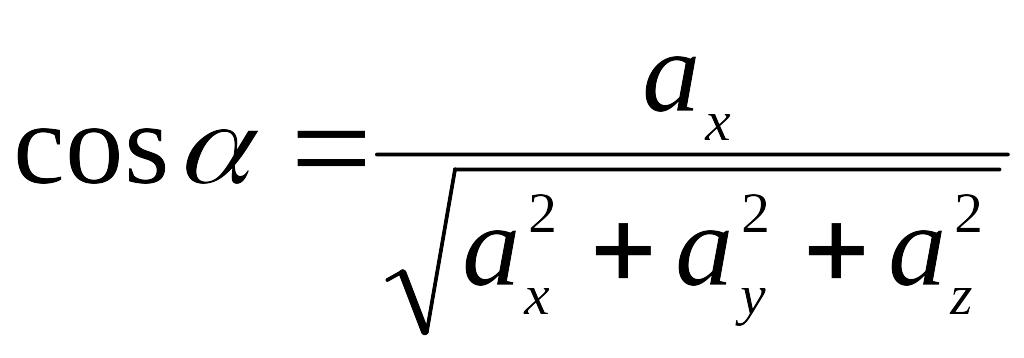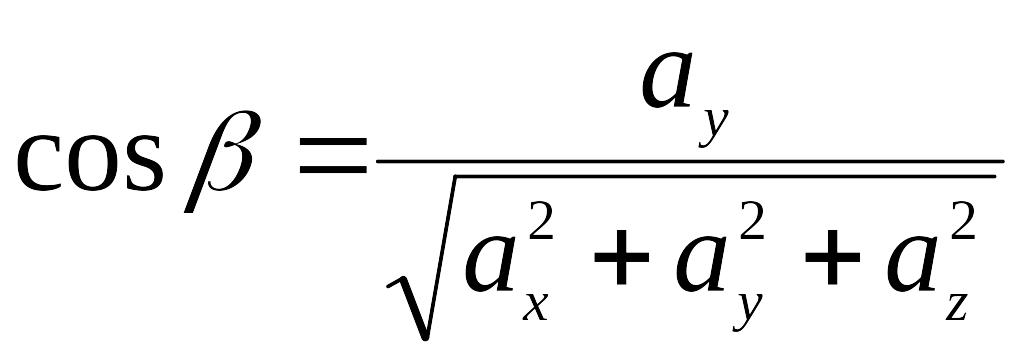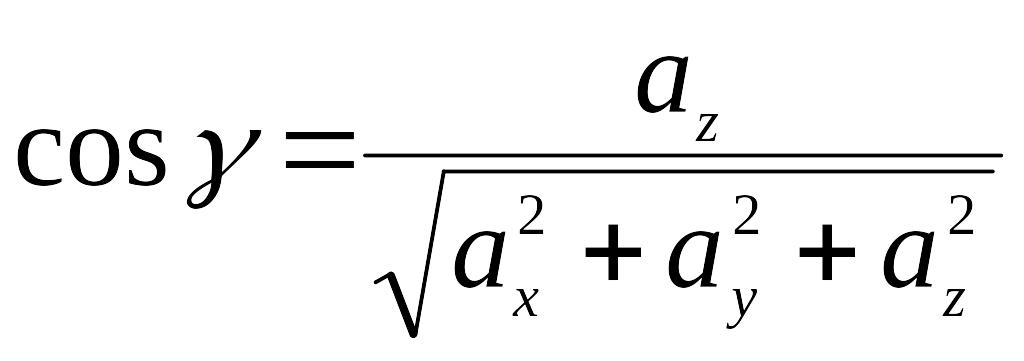, , . (2.6)

Возведём в квадрат равенства (2.6) и сложим: сумма квадратов направляющих косинусов любого вектора равна единице

.

Введём единичный вектор по направлению , для которого тогда

+ +

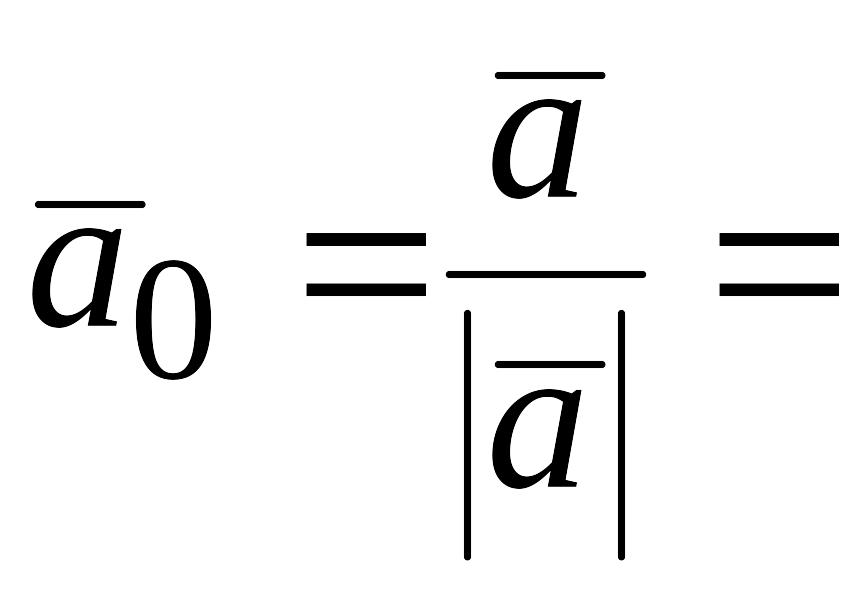
или

,

т. е. проекции единичного вектора по направлению вектора совпадают с его направляющими косинусами.

Пример. Найти единичный вектор по направлению вектора , если известны точки А(2, 2, 3), В(0, 2, 5).

Решение. Найдём вектор и его длину:

,

Вычислим направляющие косинусы:

Проверим равенство единице суммы квадратов направляющих косинусов:

Значит, единичный вектор данного направления найден верно. Запишем его координаты: .

Деление отрезка в данном отношении

Разделить отрезок в данном отношении   0  значит найти такую точку М, что

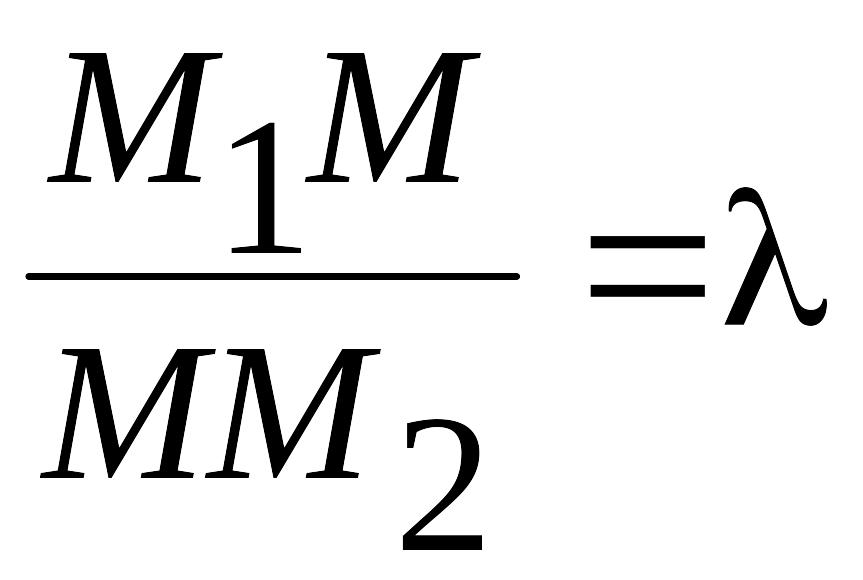
, или .

Пусть координаты точек и известны:

, .

Соединим все точки с началом координат, построив их радиус-векторы (рис. 2.19):

– радиус-вектор точки М₁,

– радиус-вектор точки М₂,

– радиус-вектор точки М.

Тогда и согласно равенству получим

, или .

Отсюда получаем формулу

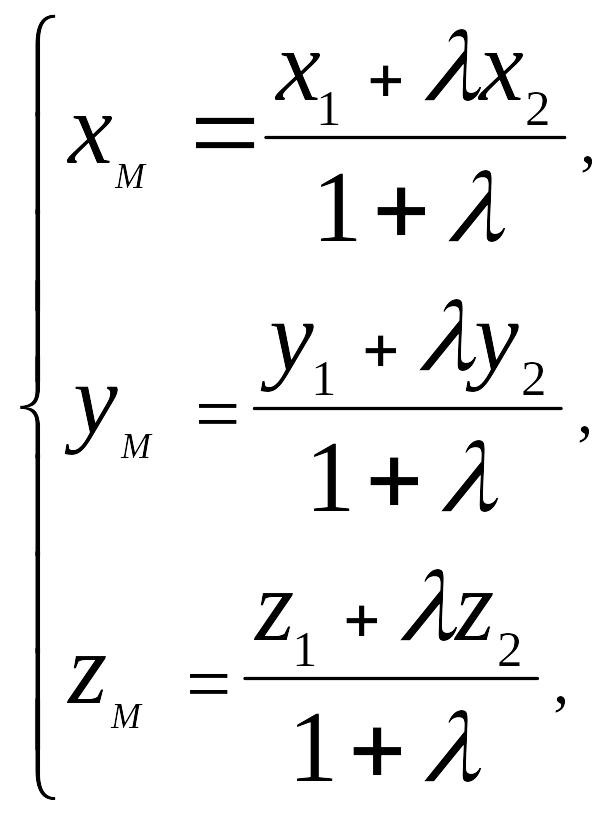
где х_М, у_М, z_M – координаты точки деления отрезка М₁М₂ в отношении .

Если точка М(х, у, z) – середина отрезка М₁М₂ ( = 1), тогда формула деления отрезка пополам:

_{а координаты середины отрезка:}

, , .