2.4. Параметрическое задание линий на плоскости
Пусть задана окружность радиуса R с центром в начале координат
x
2
+ y2
= R2.
Выберем в качестве параметра угол наклона радиуса вектора произвольной точки М(х, у) линии к оси ох (рис. 2.10). Тогда
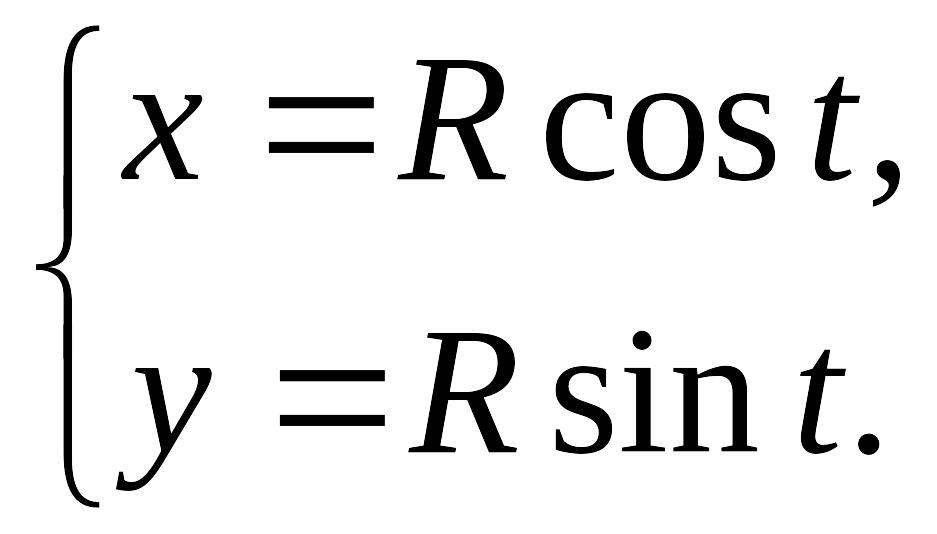
Это и есть параметрические уравнения окружности.
Пусть окружность радиуса r катится по прямой без скольжения. Примем за ось Ох (рис. 2.11) прямую, по которой катится окружность радиуса r.
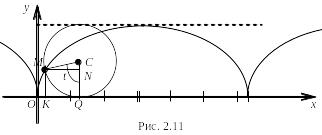
Пусть началом О координат будет та точка оси Ох, с которой совпадала текущая точка М в начальный момент движения окружности. Составим параметрические уравнения циклоиды. За параметр примем угол t, образуемый радиусом МС катящейся окружности с перпендикуляром СQ, опущенным из центра C круга на ось Ох. Определим координаты х и у точки М:
x = OK = OQ KQ,
y = KM = QC NC.
Сразу видно, что
MC = r, KQ = r sint, QC = r, NC = r cost.
Так как в начальном положении круга точка М совпадала с началом координат, то если покатить круг влево, когда он пройдёт по оси Ох путь OQ, точка М совместится с точкой О. Таким образом, путь OQ будет равен дуге МQ круга. Таким образом, OQ = МQ. Но дуга круга МQ равна rt. Следовательно, OQ = rt. Подставляя полученные значения отрезков в выражения для х и у, находим параметрические уравнения циклоиды:
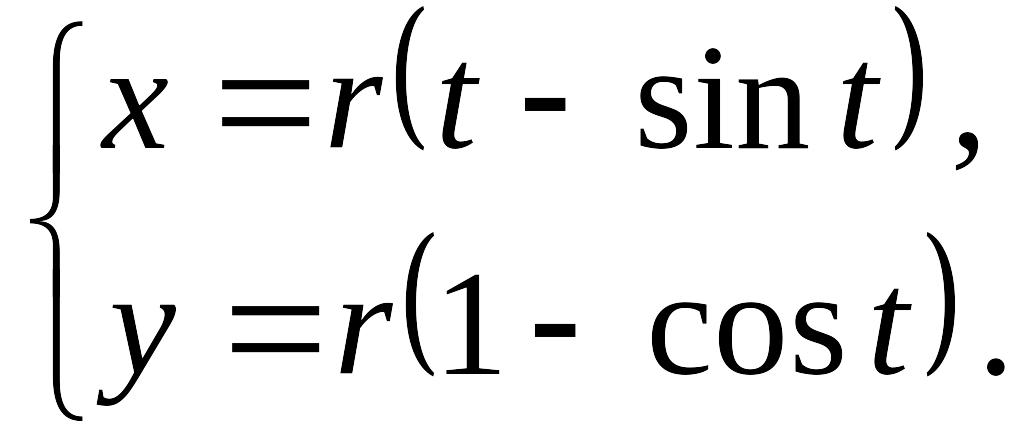
Заставляя параметр t принимать различные значения, мы заставляем точку М описывать циклоиду. Можно построить циклоиду, составив таблицу значений координат х и у её текущей точки М в зависимости от значений параметра t. Исключение параметра t приводит к декартову уравнению циклоиды. Из второго уравнения имеем
,
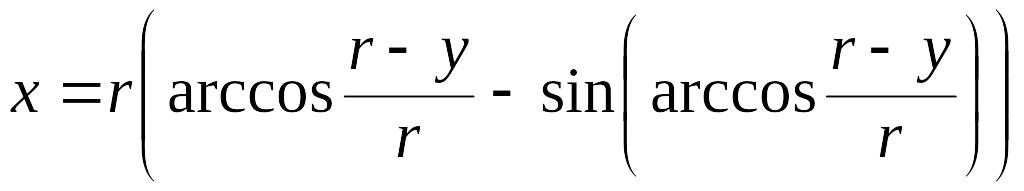или
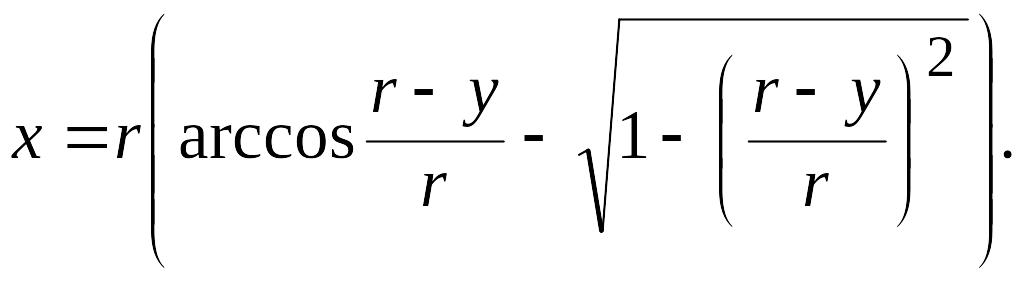
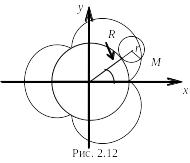
Пусть имеем две окружности разных радиусов. Точка М окружности, катящейся без скольжения по внешней стороне другой окружности, описывает эпициклоиду (рис. 2.12), уравнения которой в параметрической форме имеют вид
где R – радиус неподвижного круга, r – радиус катящегося круга, r < R; t – угол между прямой, соединяющей центры окружностей, и осью х.
Примечательна сама по себе история кривой, называемой циклоидой, сыгравшей исключительную роль в развитии математики на заре становления анализа бесконечно малых. Эта кривая описывается любой фиксированной точкой окружности, катящейся без скольжения по прямой. Таких кривых в жизни бесконечное множество: где есть катящееся колесо, там и циклоиды.
Циклоиду открыл, назвал и начал изучать Галилей. Хр. Гюйгенс изобрёл циклоидальный маятник и применил его в часах. Идею использования маятника для регулирования хода часов в 1641 г. выдвинул Галилей, но реализовать не смог ввиду наступившей потери зрения.
2.5. Векторы на плоскости и в пространстве
Такие величины, как температура, время, масса, площадь, объём и т.д., характеризуются одним числовым значением и называются скалярными. Другие величины, такие, как сила, скорость, ускорение, характеризуются числом и направлением и называются векторными. Для геометрического изображения физических векторных величин служат векторы.
Вектором называется направленный отрезок, т.е. отрезок прямой, ограниченный двумя точками, одна из которых называется начальной, а другая конечной.
Модуль вектора есть положительное число, равное длине вектора, т. е. расстоянию между его начальной и конечной точками.
Обозначение
модуля:
,
,
.
Вектор,
у которого конечная точка совпадает с
начальной, называется
нуль-вектор
и
обозначается
.
Направление
нулевого вектора не определено.
Векторы равны, если они одинаково направлены и длины их равны.
Вектор, длина которого равна единице, называют единичным вектором.
Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых.
Два коллинеарных вектора называются одинаково направленными, если их концы В и D лежат по одну сторону от прямой АС, содержащей их начала (рис. 2.13). В противном случае они называются противоположно направленными.
Два вектора, противоположно направленные, но имеющие одинаковые длины, называются противоположными.
Так,
в параллелограмме AВСD
(рис. 2.14)
векторы
и 
противоположные,
а векторы
и
– равные:
=
.
Векторы, лежащие в одной плоскости (или в параллельных плоскостях), называются компланарными.
Каков
бы ни был вектор
и точка А
в пространстве, всегда можно построить
путём параллельного переноса единственный
вектор
=
.
Вектор, точка приложения которого может быть выбрана произвольно, называют свободным.
В дальнейшем мы будем преимущественно рассматривать свободные векторы.
Умножение
вектора на число.
Произведением
вектора
на
число
называется
вектор
,
коллинеарный
вектору
,
имеющий
длину
,
одинаково
направленный с вектором
при
0
и противоположно направленный при
0.
Сложение
векторов.
Отложим
вектор
от некоторой точки А
(рис.
2.15), затем от точки В
отложим вектор
=
.
Вектор
,
соединяющий
начало первого вектора и конец второго,
называется суммой
и
обозначается
+
.
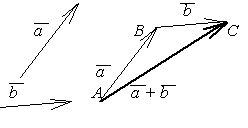
Рис. 2.15
О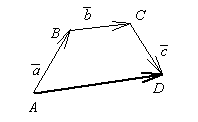
перация
сложения векторов распространяется на
любое конечное число слагаемых векторов.
Чтобы сложить три вектора
,
и
(рис. 2.16), расположим их так, чтобы
Рис.
2.16 конец первого служил началом
второго, а конец второго – началом
третьего, т. е.
,
,
.
Суммой векторов
,
и
является
вектор
,
соединяющий начало первого и конец
последнего вектора
Вычитание
векторов.
Разностью
двух векторов
и
называется
третий вектор
равный сумме векторов
и
,
если
.
1. Переместительный закон (коммутативности):
2. Сочетательный закон (ассоциативности):
3. Нулевой вектор играет роль нуля на множестве векторов:
4. Сумма противоположных векторов равна нуль-вектору:
5. Если каждый из векторов умножить на число , то и сумма этих векторов умножится на число :
Проекция вектора на ось
Проекция
вектора
на ось l
обозначается
символом
.
Проекция вектора на ось l равна произведению модуля вектора на косинус угла между вектором и осью:
.
Линейная зависимость векторов
Система
векторов
называется
линейно
зависимой,
если
существуют числа
,
не все равные нулю, для которых справедливо
равенство
. (2.2)
Левая
часть
равенства
(2.2)
называется
линейной
комбинацией векторов
.
Векторы
называются
линейно
независимыми,
если
равенство (2.2)
выполняется только при
.
Если система векторов линейно зависима, то хотя бы один из векторов всегда можно представить в виде линейной комбинации остальных:
. (2.3)
Справедливо и обратное: если один из векторов представлен в виде линейной комбинации остальных, то эта система векторов линейно зависима.
Всякие три вектора , и , принадлежащие одной плоскости, линейно зависимы.
Для того чтобы три вектора в трёхмерном пространстве были компланарны, необходимо и достаточно, чтобы они были линейно зависимы. Если три вектора не компланарны, то они линейно независимы.
Пример. Даны
точки А,
В, С.
Показать, что вектор
коллинеарен вектору
.
Решение.
Преобразуем сумму:
=
Пусть
,
,
тогда
,
,
следовательно, векторы
коллинеарны.
Базисом на плоскости называются любые два линейно независимых вектора.
Пусть
– любой
вектор на плоскости,
и
– базис,
то
.
Говорят, что вектор
разложен по базису
,
;
числа
и
называются аффинными
координатами
вектора
на плоскости:
.
В трёхмерном пространстве базисом называются любые три линейно независимых вектора, т. е. всякие три некомпланарных вектора.
Пусть
, 
,
– базис.
Тогда любой четвёртый вектор можно
представить в виде их линейной комбинации
,
или
,
где
–
координаты
вектора
в
базисе
,
,
.
Если векторы , , , имеют общее начало в точке О и точка М является концом вектора , то вектор
= 
называется
радиус-вектором
точки
М в
базисе
,
,
,
при этом числа
называются аффинными
координатами
точки
М.