Методичні рекомендації

При підготовці до роботи необхідно:

• Ознайомитися з цілями, завданнями і змістом лабораторної роботи.

• Вивчити теоретичні відомості до роботи.

• Підготувати початкові дані до лабораторної роботи відповідно до індивідуального варіанту.

• Підготувати додаткові початкові дані до лабораторних завдань.

• Пройти вхідне тестування або опитування для допуску до лабораторної роботи.

Початковими даними до лабораторної роботи є значення частоти тестового сигналу (F = f_0i) і частоти дискретизації сигналу f_д. Їх вибирають з приведених в таблиці 1, таблиці 2, таблиці 3 технічних характеристик цифрових фільтрів для заданої викладачем багатоканальної системи ЦОС конкретного виду згідно з вказівками.

Нижче наведений приклад вибору початкових даних для системи багатоканального смугового аналізу і синтезу сигналів (ЦОС РЛС) радіолокацій, варіант v = 20, число каналів системи К = 20.

Початкові дані знаходяться по таблиці. 3. Варіанту v = 20 відповідають f_0i = 1 050 Гц, f_д = 4 000 Гц.

До додаткових даних для виконання лабораторних завдань відносяться:

• значення частоти дискретизації f_да сигналу x(lT_да), що моделює заданий аналоговий сигнал x(t);

• число вибірок N дискретного сигналу x(nT_д), необхідне для його аналізу в часовій і частотній області.

Частота дискретизації f_да = 1/T_да квазіаналогового сигналу x(lT_да) знаходиться з умови перевищення нею у декілька разів частоти дискретизації f_д заданою для досліджуваного дискретного сигналу x(nT_д): f_да = Мf_д. Значення коефіцієнта М вибирається в межах М = 20...50.

Необхідне значення числа вибірок N дискретного сигналу x(nT_д) повинне задовольняти умові розміщення на довжині аналізованої реалізації NТ_д цілого числа р його періодів T = 1/F: NT_д = pT. Їм забезпечується однозначний дозвіл спектральних складових сигналу при обчисленні їх амплітуд X_mk і фаз φ_k за допомогою дискретного перетворення Фур'є (ДПФ), яке виконується на дискретних частотах f_к = kF = kf_0i, k = 0, 1, …(N/p) - 1:

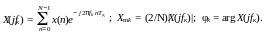
Числу вибірок сигналу N, по якому обчислюється ДПФ, відповідає крок аналізу по частоті Δf_а = f_д/N.

Для знаходження N співвідношення NT_д = pT представляється у вигляді

f_д / f_0i = N / p.

Як N приймається найменше число, що задовольняє цьому співвідношенню при усіх значеннях частот f_0i, i = 1, 2,... K, де K - число каналів багатоканальної системи ЦОС. При цьому число періодів сигналу р залежатиме від f_0i.

Наприклад: f_д = 7 680 Гц; f_0i = 240 + i240, Гц

f_д / f_0i =7 680 / (240 + i240) = 32 / (1 + i) = N/ p_i; N = 32; p_і = 1 + i.

Крок аналізу по частоті при цьому рівний: Δf_а = f_д/N = 240 Гц. Значенню цього кроку кратні як усі задані частоти f_0i = (i +1) Δf_а, так і їх вищі гармоніки.

Таким чином, в цьому прикладі умовам аналізу сигналів в часовій і частотній області для усіх варіантів відповідає мінімальне значення числа вибірок N = 32. При збільшенні його в кратне число разів пропорційно зменшується і крок аналізу сигналу по частоті.

Примітка: для системи цифрової обробки аудіосигналів (ЦОАС) вибір N проводиться окремо для кожного з її частотних піддіапазонів l = 1, 2,.6, що включають 4 канали з однаковою частотою дискретизації f_дl.

Для аналізу сигналу x(lT_да) з частотою дискретизації f_да = Мf_д, моделюючого аналоговий сигнал x(t), число його вибірок N_а повинне перевищувати знайдене значення N для сигналу x(nT_д) в М разів: N_а = N  M.

Вибрані значення N, N_а в програмі SDCAD називаються шириною вікна аналізу і вводяться в якості параметрів аналізу для кожної контрольної точки. Максимально можливе значення довжини аналізованої реалізації(ширина вікна) в програмі SDCAD складає 3 999.

Значення ширини вікна аналізу N_а можна використати і при аналізі спектру сигналу з частотою дискретизації f_д (замість N), при цьому крок аналізу по частоті зменшиться в M разів і в M разів зросте число періодів сигналу на довжині реалізації.