Лабораторна робота 1 дослідження перетворень спектрів при дискретизації сигналів після часу і відновлення

Мета лабораторної роботи: закріплення теоретичних знань про перетворення сигналів з аналогової форми в цифрову і з цифрової в аналогову шляхом їх моделювання на ЕОМ.

Завдання лабораторної роботи :

• вивчення спектрів дискретних сигналів, їх особливостей, взаємозв'язку;

• спектрів дискретних і аналогових сигналів, умов вибору частоти дискретизації для різного виду сигналів;

• дослідження перетворень частот при дискретизації періодичних сигналів, що не відповідають теоремі відліків;

• дослідження явища підміни частот і накладення спектрів при дискретизації сигналів;

• дослідження спотворень, що виникають при відновленні сигналів(цифро-аналоговому перетворенні).

Програмне забезпечення лабораторної роботи. Лабораторна робота виконується за допомогою програми структурного моделювання алгоритмів і систем ЦОС SDCAD. Опис програми приведений в дод. 1.

Короткі теоретичні відомості

Лабораторна робота виконується на основі теоретичного матеріалу, викладеного в главі 1 навчального посібника [1].

Дискретний сигнал х(nТд) (рис. 1) відповідає вибіркам аналогового сигналу x(t) в дискретні рівновіддалені моменти часу t = nТ_д = n/f_д : x(nT_д) = x(t) | t = nT_д, де Т_д = 1/f_д − період дискретизації сигналу за часом, f_д − частота взяття вибірок, що називається частотою дискретизації, n = 0, 1, 2, ... - номер вибірки.

Рис. 1.1. Графіки безперервного х(t) і дискретного х(nT_д) (х(n)) сигналів

Наприклад, аналоговому сигналу x(t) = Х_mcos(ωt + ) відповідає дискретний сигнал х(nТ_д) = Х_mcos(ω_nT_д + ) = Х_mcos[2π (f/f_д) n + )].

Дискретний сигнал означають також функцією номера вибірки n : х(nТ_д) = х(n) (рис. 1.1).

Спектр (перетворення Фур'є) дискретного сигналу знаходиться як . Він зв'язаний із спектром аналогового сигналу співвідношенням . Спектроперіодичний по частоті і дорівнює сумі зміщених на kω_д спектрів аналогового сигналу (рис. 1.2, 1.3).

При максимальній частоті спектру аналогового сигналу ω_m1, що відповідає умові ω_m1 ≤ ω_д/2 (рис. 1.2), спектри дискретного і аналогового сигналів співпадають в основній смузі частот 0 ± ω_д/2 (при |ω|≤ ω_д/2) : Х(jω) = Х_а(jω). Умова ω_m ≤ ω_д/2 (чи ω_д ≥ 2ω_m) відповідає теоремі відліків Котельникова.

При ω_m2 > ω_д/2 (рис. 1.3) відбувається накладення (перекриття) сусідніх копій спектру і Х(jω) ≠ Х_а(jω) в смузі 0±ω_д/2. При цьому складові спектру аналогового сигналу з частотою F, f_д/2, що перевищує, трансформуються в основну смугу частот дискретного сигналу 0± f_д/2. Вони перетворяться в нові спектральні складові з частотою

F_пр = |F - f_д [F/f_д]_цч.окр|,

де індекс «цч.окр» означає взяття цілої частини з округленням.

Рис. 1.2. Спектральні перетворення при дискретизації аналогового сигналу з фінітним спектром при ω_д ≥ 2ω_m

Рис. 1.3. Спектральні перетворення при дискретизації аналогового сигналу з фінітним спектром при ω_д < 2ω_m

Короткі теоретичні відомості

При F < f_д [F/f_д]_цч.окр змінюється також знак початкової фази сигналу : _пр = π - .

Наприклад, при f_д = 1 000 Гц і F₁ = 750 Гц отримуємо F_пр1 = 250 Гц, _пр1 = π-₁. При F₂ = 1 250 Гц отримуємо F_пр2 = 250 Гц, але _пр2 = ₂.

Для аналогових сигналів з необмеженим по частоті, але спадаючим спектром явище накладення спектрів має місце при будь-якому значенні частоти дискретизації f_д. Її значення вибирають виходячи з допустимого рівня спотворень накладення по частоті спектру f_m, що умовно приймається за максимальну: f_д ≥ 2f_m.

Перетворення цифрового сигналу в аналоговий (відновлення сигналу) здійснюється за допомогою цифроаналогового перетворювача (ЦАП) і згладжуючого ФНЧ (рис. 1.4).

Рис. 1.4. Структура підсистеми відновлення сигналу

У частотній області відновлення полягає у виділенні з мінімальними спотвореннями основної смуги спектру цифрового сигналу 0± f_д/2 і придушенні усіх його періодичних копій (рис. 1.2), тобто у деперіодизації сигналу.

Рис. 1.5. Сигнали підсистеми відновлення сигналу

Сигнал ŷ(t) на виході ЦАП має вигляд сходинок тривалістю Т_д (рис. 1.5).

Спектр такого сигналу визначається як Ŷ (jω) = H_ЦАП( jω) Y_ц( jω) (t) (t). Частотна характеристика ЦАП H_ЦАП(jω) є перетворенням Фур'є його імпульсної характеристики h_ЦАП(t) = 1 при 0 ≤ t ≤ Т_д. Модуль частотної характеристики (АЧХ)

|H_ЦАП(jω) | = |sin(ωТ_д/2) / (ωТ_д/2)|

має нульові значення на частотах ω = kω_д, k = ±1, ±2,. і значення 1; 0,89; 0,65 на частотах ω = 0, ω_д/4_, ω_д/2 (рис. 1.6). Максимуми бічних пелюсток АЧХ убувають за законом функції (sin x) / x.

Наклавши АЧХ ЦАП на спектр дискретного сигналу (рис. 1.6), можна оцінити спотворення, що виникають при відновленні сигналу і визначити вимоги до частотної характеристики ФНЧ.

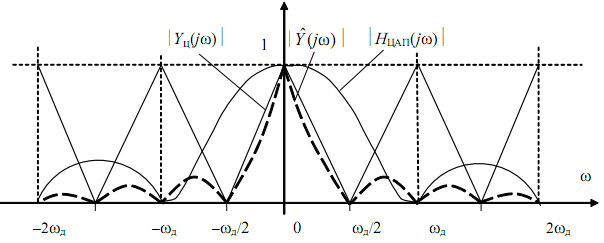
Рис. 1.6. Частотна характеристика ЦАП |Н_ЦАП(jω) | і перетворення спектру при цифроаналоговому перетворенні

При моделюванні на ЕОМ дискретизації сигналів за часом як модель аналогового сигналу x(t) приймається дискретний сигнал x(lT_да) з частотою дискретизації f_да = 1/T_да, що перевищує у декілька разів задану частоту дискретизації f_д для досліджуваного дискретного сигналу x(nT_д): f_да = Мf_д, М = 20...50 (рис. 1.7). При цьому перехід від дискретного сигналу x(lT_да), моделюючого x(t), до дискретного сигналу x(nT_д) здійснюється шляхом зниження частоти дискретизації f_да в М разів простим проріджуванням вибірок сигналу x(lT_да).

Моделювання відновлення сигналу здійснюється шляхом підвищення частоти дискретизації f_д дискретного сигналу y(nT_д) в М разів до частоти f_да = Мf_д шляхом додавання (М-1)-ої нульових вибірок на кожному інтервалі дискретизації і подальшої обробки його за допомогою цифрового фільтру-інтерполятора нульового порядку з прямокутною імпульсною характеристикою завдовжки М (рис. 1.8).

Рис. 1.7. До моделювання дискретизації сигналу в часі

Рис. 1.8. До моделювання відновлення сигналів

Частотна характеристика такого фільтру практично співпадає з частотною характеристикою ЦАП при значенні М = 20…50.