3.3. Учебное пособие

1. Голик, Е.С. Математические методы системного анализа и теории принятия решений: учеб. пособие. Ч.1. /Е.С. Голик [и др.]. – СПб.: Изд-во СЗПИ, 1999. – 54 с.

2. Голик, Е.С. Математические методы системного анализа и теории принятия решений: учеб. пособие. Ч.2. /Е.С. Голик. – СПб.: Изд-во СЗТУ, 2002. – 102 с.

3.4. Технические средства обеспечения дисциплины

1. Компьютерная программа Mathcad Professional.

2. Компьютерная программа Statgraphics.

3.5. Методические указания к проведению практических занятий

Практические занятия предусматривают решение задач по всем разделам дисциплины. Ниже приводятся задачи с решениями по каждому разделу.

Практическая работа № 1

Задача

Вычислить продолжительность пути, ведущего от основного события к 6-му событию, если сетевая модель имеет характеристики, представленные на рис. 1.1.

Рис. 1.1. Сетевая модель

Решение

Продолжительность максимального пути, ведущего от основного собы­тия к k-му:

(1.1)

где нулем обозначен номер исходного события.

Напишем формулу для вычисления . Обозначим через множество дуг (i,j), входящих в j-ю вершину (событие), и допустим, что все значения для j-х событий, которыми на­чинается каждая из этих дуг (работ), нами уже вычислены. То­гда на основании формулы (1.1) можем написать:

(1.2)

где N – номер завершающего события, причем = 0.

Вычисляя с помощью формулы (1.2) значения (вычисле­ния ведутся последовательно от исходящего события к завершаю­щему), найдем для нашей сетевой модели (рис. 1.1):

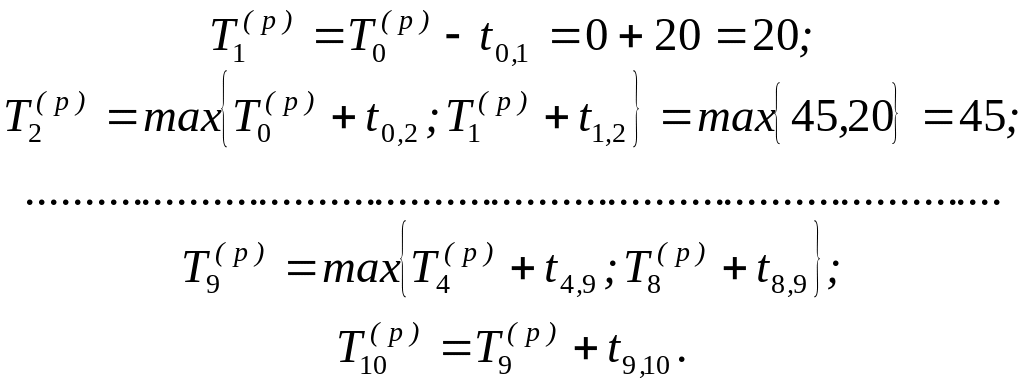
Вычислив все значения , получим . Ранний срок наступления завершающего события определяет продолжительность критического пути:

. (1.3)

Поздний срок наступления события – это самый поздний из допустимых моментов наступления данного k-го события, при котором еще возможно выполнение всех последующих работ без превышения критического времени. Превышение позднего срока на некоторую величину приводит к аналогичному увеличению кри­тического времени. Значение определяется как разность между критическим временем и продолжительностью максимального пути, ведущего от данного события к завершающему:

. (1.4)

Например, от события 6 (рис. 1.1) к завершающему событию ведут два пути: 6–7–8–9–10 с продолжительностью 195 ед. и 6–8–9–10, продолжительность которого равна 200 ед. Согласно формуле (1.4) . Очевидно, что если событие 6 наступит в момент (тo есть позднее ), а на выполнение работ, составляющих путь 6–8–9–10, требует­ся 200 ед., то в результате завершающее событие наступит в мо­мент, превышающий Т_кр на столько, на сколько больше . Действительно, вычислим поздний срок наступления события 6 как разность между Т_кр и продолжительностью первого пути: = Т_кр–195 = 305–195 = 110 ед. С этого момента требуется еще 200 ед. времени на выполнение работ второго пути, следовательно, завершающее событие наступит через 110+200=310 ед. после на­чала работ, то есть T_кр будет превышено на 5 ед.

Практическая работа № 2

Задача

По сетевому графику рис. 2.1 рассчитать резерв времени событий и работ.

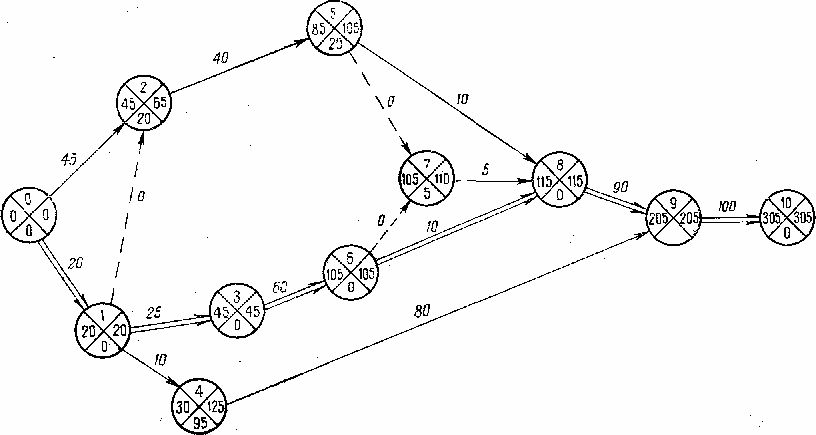
Рис. 2.1. Сетевой график

Решение

В левый сектор исходящего события сразу записывается значение T₀^(p) = 0. Далее находим: к событию 1 под­ходит одна дуга (0, 1), поэтому T₁^(p) = 0+20 = 20; к событию 2 под­ходят две дуги (0, 2) и (1, 2), поэтому T₂^(p) = max{0+45; 20+0}=45, и так далее. Каждое вычисленное значение T_k^(p) сразу записывает­ся в соответствующий сектор.

Поздний срок наступления завершающего события согласно формуле = T_кр. равен раннему сроку, эту величину записывают в правый сектор и далее ведут расчет последовательно от завершаю­щего события к исходящему.

Для нашего сетевого графика имеем T₁₀⁽ⁿ⁾ = T₁₀^(p) =305. Далее находим: из событий 9, 8, 7 выходит по одной дуге, поэтому T₉⁽ⁿ⁾ = 305–100 =205; T₈⁽ⁿ⁾ =205–90=115; T₇⁽ⁿ⁾ =115–5=110; из со­бытия 6 выходят две дуги (6, 7) и (6, 8), поэтому T₆⁽ⁿ⁾ = min{110–0; 115–10} =105 и так далее.

После того, как рассчитаны все значения T_k⁽ⁿ⁾, вычисляют ре­зервы времени событий как разности между величинами, записан­ными в левых и правых секторах, и записывают их в нижние сек­торы. Остальные параметры сетевой модели вычисляют по форму­лам (1.11)–(1.17) [2] (с. 16-17). Результаты всех расчетов удобно представить в виде табл. 2.1.

Таблица 2.1.

Началь­ное со­бытие i	Конеч­ное со­бытие j	Tij			Rij
0	1	20	20	20	0	0	0
0	2	45	45	65	20	20	0
1	2	0	45	65	20	45	25
1	3	25	45	45	0	0	0
1	4	10	30	125	95	95	0
2	5	40	85	105	20	20	0
3	6	60	105	105	0	0	0
4	9	80	205	205	0	95	95
5	7	0	105	110	5	25	20
5	8	10	115	115	0	20	20
6	7	0	105	110	5	5	0
6	8	10	115	115	0	0	0
7	8	5	115	115	0	5	5
8	9	90	205	205	0	0	0
9	10	100	305	305	0	0	0

Критический путь проходит через события, для которых R_j=0 (0–3–6–8–9–10).

Практическая работа № 3

Задача

На пункте технического обслуживания (ПТО) оборудованы две линии по обслуживанию техники. Время обслуживания одной еди­ницы техники распределено по показательному закону с парамет­ром Число единиц техники, одновременно находящихся на ПТО, не должно превышать четырех единиц. Поток техники на обслуживание – простейший поток заявок интенсивности =0,5ед./ч. Определить показатели эффективности работы ПТО.

Решение

Анализ задачи показывает, что ПТО можно рас­сматривать как СМО с конечной очередью, параметры которой n=2, m=2, =0,5 ед./ч, =0:5 ед./ч, = 1, =0,5.

Результаты вычислений для различных значений п и т (раз­личных вариантов организации ПТО) приведены в табл. 3.1.

Расчет показателей СМО целесообразно производить в после­довательности, указанной в таблице. Если =1 (для п=1, m=3), то Р₀ и L рассчитывают непосредственно по формулам (2.25) и (2.31) [2] (с. 41, 42).

Из полученных данных видно, что уменьшение п при постоян­ном значении п+т=4 позволяет значительно (в 1,7 раза) повы­сить коэффициент загрузки линий K_з Однако эффективность об­служивания техники значительно снизилась: при п=1 каждая пя­тая машина (Р_отк=0,2) уходит с ПТО необслуженной, а при n=2 только одна из 25 машин (Р_отк=0,044) получает отказ; среднее время пребывания машины на ПТО при n=1 , а при п=2 .

Таблица 3.1

Показатели	п=2, т= 2	п=1, т= 3	п=2, т=0	п=2, т
Р0	0,348	0,2	0,4	0,333
Pож	0,304	0,8	–	0,333
Ротк	0,044	0.2	0,2	0
q = 1–Ротк	0,956	0,8	0,8	1,0
Q (ед./ч)	0,478	0,4	0,4	0,5
Nз (ед.)	0,956	0,8	0,8	1,0
Кз (%)	47,8	80	40	50
L (ед.)	0,174	1,2	–	0,333
(ч)	0.348	2,4	–	0.666

Исключение очереди на ПТО (п=2,т=0) приводит к значи­тельному возрастанию вероятности отказа (с 0,044 до 0,2). Отсут­ствие ограничения на длину очереди (п=2, m) несколько по­вышает загрузку линий, однако приводит к увеличению времени ожидания почти в два раза (с 0,348 до 0,666 ч). Для этого случая целесообразно определить вероятность того, что число машин, одновременно находящихся на ПТО, превышает 4:

,

то есть пятую часть времени на ПТО находится более четырех ма­шин одновременно.

Практическая работа № 4

Задача

Техническая система состоит из n=10 ти­пов элементов, суммарная интенсивность потока отказов элементов каждого типа , интенсивность потока отказов системы . Определить состав комплекта ЗИПа, необходимого для обеспечения нормального функционирования си­стемы в течение времени T=1000 ч с вероятностью R_д ==0,95.

Решение

Оптимальный состав комплекта ЗИПа можно определить по следующей методике.

Определить объем запасов так, чтобы их стоимость была минимальной, то есть

(4.1)

а вероятность его достаточности R(Y) была не ниже заданной R_д, то есть

, или (4.2)

и выполнялись ограничения по суммарному весу запасов и требуемой емкости склада:

, (4.3)

где G — допустимый вес запасов; V — ограничение на емкость склада.

Определить объем запасов V* так, чтобы

(4.4)

или

(4.5)

и выполнялись условия

, (4.6)

где С_д — объем средств, выделяемых на создание запасов в каж­дом периоде.

Если ограничение на вес запасов и (или) емкость склада не на­кладывается, то соответствующие неравенства в (4.3) или (4.6) не учитываются.

Рассмотренная математическая модель управления запасами широко используется при определении состава комплектов ЗИПа, для технических систем. В этом случае у_j – количество запасных элементов j-го типа, a R(Y) – вероятность достаточности комп­лекта ЗИПа или вероятность нормального функционирования тех­нической системы (без простоев из-за недостачи запасных эле­ментов) .

Вышеприведенная теория применима, если если заданы стоимостные, весовые и габаритные характеристики элементов системы, а также требования к стоимостным (минимум стоимости), весовым G и га­баритным V характеристикам комплекта ЗИПа.

Если указанные характеристики не заданы, то рациональный состав комплекта ЗИПа определяют из условия обеспечения рав­ной вероятности достаточности запасных элементов каждого типа («равнопрочный» ЗИП). Решение задачи производится в следую­щем порядке.

1. Определить требуемые значения вероятности достаточности r_j(y_j) или недостаточности q_j(у_j) из условия

.

Для рассматриваемого примера

.

2. Вычислить среднее ожидаемое число требований на элемен­ты каждого типа:

.

3. По формуле методом последовательных приближений определить минимальное количество запасных элементов каждого типа, необходимых для обеспечения требуемого значения r_j (у_j).

Так, для рассматриваемого примера ; , то есть в состав комплекта ЗИПа доста­точно включить по одному элементу каждого типа (всего 10 эле­ментов).

Рассчитаем состав группового комплекта ЗИПа, необходимого для эксплуатации W=5 одинаковых систем для условий рассматриваемого примера. В этом случае . Для обеспечения в состав комплекта ЗИПа необходимо включить по три запасных элемента каждого типа (всего 30 элементов). Следовательно, создание группового комплекта позволяет уменьшить объем запаса в расчете на одну систему в 10:(30:5)=1,67 раза.

Пусть за счет применения однотипных элементов удалось сократить количество типов элементов до n=5, интенсивность потока отказов системы осталась прежней, то есть .

Для обеспечения вероятности в состав индивидуального комплекта необходимо включить по два элемента каждого типа (всего 10 элементов), так как

,

а в состав группового комплекта на W=5 систем – по четыре элемента каждого типа (всего 20 комплектов). Групповой комплект эффективнее индивидуального в 10:(20:5)=2,5 раза. Уменьшение числа типов элементов позволило сократить объем запаса в групповом комплекте в 30:20=1,5 раза. Таким образом, при простейшем потоке требований на предметы запаса целесообразно увеличение количества потребителей, обслуживаемых одним складом (создание групповых комплектов ЗИПа), и уменьшение числа используемых номенклатур (числа ЗИПов элементов в технических системах).

Практическая работа № 5

Задача

Пусть R выражает мне­ние ЛПР о том, что частный показа­тель Wi не менее предпочтителен, чем показатель Wj, для векторного показателя W=(W1, W2, W3, W4), где W1 — покупательная способность; W2 — себестоимость; W3 — затраты; W4 — время на реализацию страте­гии. ЛПР, например, считает, что увеличение покупатель­ной способности не менее предпочти­тельнее снижения себестоимости и затрат, а снижение себестоимости, в свою очередь, не менее предпочти­тельнее снижения затрат (при усло­вии, что затраты не превышают допу­стимой нормы); фактор времени при этом не менее важнее снижения себе­стоимости и затрат. Причем отношение R для слу­чая, изображенного на рис. 5.1, а, полученное в результате опроса эк­спертов, представляется в виде фун­кции принадлежности:

1 0,9 0,6 0,6

µ_R = 0,1 1 0,7 0,2

0,4 0,8 0,7 1 .

Представить отношение r в виде графа; матрицы смежности и множеством точек в декартовой системе координат. Решение

В этом случае от­ношение R можно записать:

R = {(W_i, W_j)\(W₁, W₁ ), (W₁, W₂),

(W₁ W₃,), (W₂, W₂), (W₂, W₃),

(W_3, W₃), (W₄, W₂), (W₄, W₃) (W₄, W₄)}

— как прямое перечисление показа­телей, связанных введенным отноше­нием;

R= {(W_i, W_j)│W_i, W_j W; W_i не менее предпочтительнее (важнее), чем W_j}— как указание общих свойств элементов.

Это же отношение может быть пред­ставлено в виде графа, матрицы смеж­ности и множеством точек в декартовой системе координат (соответственно слу­чай а—в на рис. 5.1); направление стре­лок на рис. 5.1, а соответствует направ­лениям рассматриваемого предпочте­ния между элементами, которые они связывают. Петли на графе обозначают тот факт, что элемент не менее пред­почтителен самого себя.

С использованием указанных спо­собов графического представления от­ношений весьма удобно анализировать их свойства. Для формального опи­сания свойств бинарных отношений обозначим: (d!, d") R или d'Rd" — если элементы d', d" связаны отноше­нием R и (d', d") R или d' "| Rd" — если элементы не связаны отноше­нием R. Заметим, что если ЛПР считает, что факт превос­ходства в важности имеет место при значениях функции принадлежности µ_R 0,5, то модель предпочтения можно представить «четкой» аппрокси­мацией, изображенной на рис. 5.1.

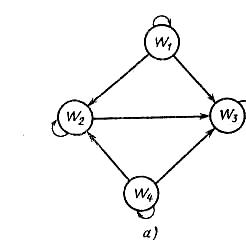
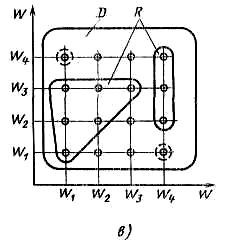
Рис. 5.1. Графическое представление бинарного отношения «не менее

предпочтителен (важен)»

Приведенная матрица соответствует случаю, когда при попарном сравне­нии элементов накладывается допол­нительное условие нормировки, из которого следует, что µ_R (d, ) = 1 – µ_R (d', d). В общем случае элементы матрицы смежности [А_д] мо­гут быть свободны от этого ограниче­ния.

По аналогии с обычным отношением нечеткое отношение можно предста­вить ориентированным графом, каж­дой дуге которого приписано число µR, или же поверхностью в декартовой си­стеме координат.

Практическая работа № 6

Задача

Решить игру в чистых стратегиях, заданную платежной матрицей

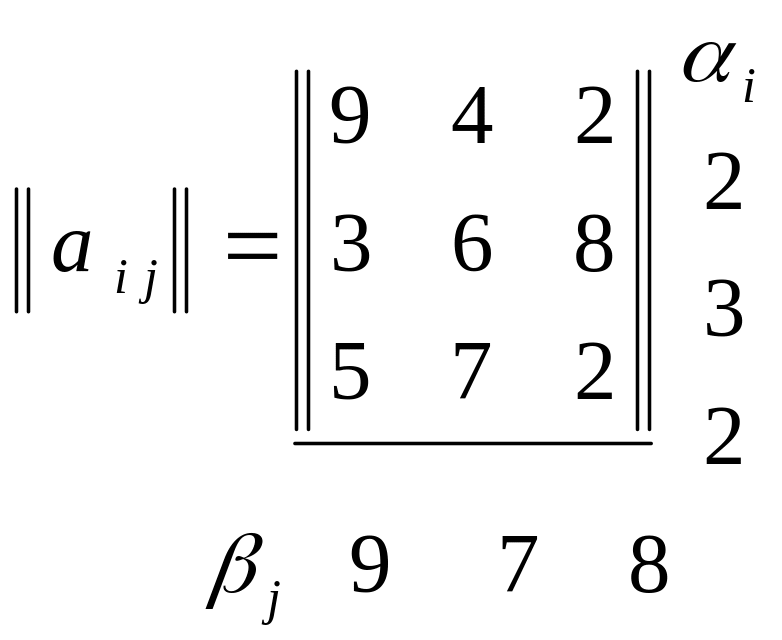
Решение

Максиминная стратегия — , минимаксная стратегия — . Минимаксные стратегии обладают свойством неустойчивости, которое заключается в изменении цены игры, если системы отклоняются от своих оптимальных стратегий. В рассмотренном примере, если известно, что система придерживается стратегии , системе целесообразно выбрать стратегию , что уменьшит ее проигрыш до трех единиц. Тогда система , если ей известно, что система намерена применить стратегию , может выбрать стратегию , что увеличит ее выигрыш до девяти единиц, и т. д.

Существует класс игр, для которых нижняя цена игры равна верхней. В этом случае цена игры

. (6.1)

Так как максимальный выигрыш одной системы равен минимальному проигрышу другой, то геометрически величина соответствует седловой точке функции, подобной функции Лагранжа. Игры, для которых справедливо выражение (6.1), называются играми с седловой точкой.

Практическая работа № 7

Задача

Решить игру в чистых стратегиях, заданную платежной матрицей:

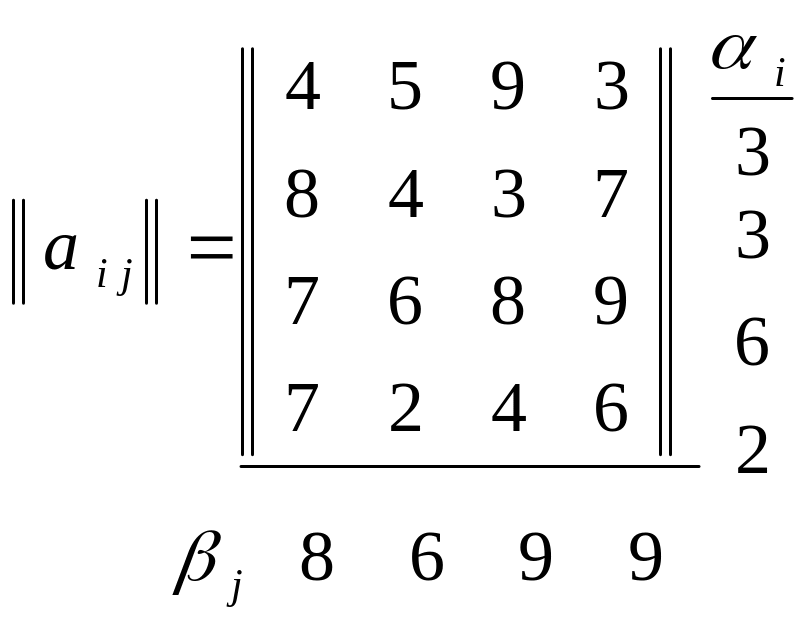
Решение

Оптимальные стратегии игр с седловой точкой устойчивы, так как отклонение любой системы от оптимальной стратегии приводит к уменьшению выигрыша (увеличению проигрыша).

Решение игры в чистых стратегиях предполагает, что каждая система при многократном повторении игры выбирает оптимальную стратегию с вероятностью 1. Стратегия системы, заключающаяся в выборе чистых стратегий с некоторыми фиксированными вероятностями, называется смешанной стратегией. Тогда чистая стратегия будет частным случаем смешанной стратегии, в которой вероятность применения всех стратегий, кроме данной, равна 0. Если игра ведется в смешанных стратегиях, то при многократном повторении игры каждая система случайно выбирает одну из своих чистых стратегий в соответствии с ее вероятностью. Смешанную стратегию системы будем описывать -мерным вектором:

,

где – вероятность использования чистой стратегии .

Смешанную стратегию системы будем описывать -мерным вектором:

,

где – вероятность использования чистой стратегии .

Очевидно, компоненты векторов и должны удовлетворять соотношениям

, (7.1)

так как множество стратегий представляет собой полное множество непересекающихся событий при назначении вероятностей , а множество стратегий – множество непересекающихся событий при назначении вероятностей .

При использовании смешанных стратегий величина выигрыша в каждой отдельной игре представляет собой случайную величину. Поэтому результат игры будет зависеть от смешанной стратегии системы и смешанной стратегии системы , который получил название платежной функции . Физически платежная функция является математическим ожиданием результата игры и вычисляется по формуле

. (7.2)

Пусть в игре существует такая смешанная стратегия системы , такая смешанная стратегия системы и такое число , что имеют место соотношения для любого ; для любого , удовлетворяющего формуле (7.1). Тогда стратегии и называются оптимальными стратегиями, число — ценой игры, а совокупность — решением игры.

Из формул (7.1) и (7.2) следует зависимость

. (7.3)

Заменяя в неравенствах число его значением из выражения (7.3), получим

. (7.4)

Точка , удовлетворяющая условиям (7.4), называется седловой точкой функции при и , удовлетворяющих условиям (7.1). Если , – числа в окрестности точки , поверхность напоминает седло, отсюда и возник термин «седловая точка». Таким образом, оптимальные стратегии систем – это седловая точка платежной функции, а цена игры – значение платежной функции в седловой точке.

Выражение (7.4) представляет собой содержание основной теоремы теории матричных игр, которая гласит: «Каждая матричная игра с нулевой суммой имеет решение в чистых или смешанных стратегиях».

Решение матричной игры в смешанных стратегиях, то есть нахождение седловой точки платежной функции (7.2), связано с операциями над платежной матрицей. Поэтому перед решением игры целесообразно упростить платежную матрицу, оставив в ней только те элементы, которые соответствуют существенным стратегиям. Чистая стратегия называется существенной, если вероятность ее использования в смешанной стратегии больше 0. В противном случае чистая стратегия называется несущественной.

Для выявления существенных стратегий попарно сравнивают строки и столбцы платежной матрицы. Если все элементы -й строки платежной матрицы не меньше соответствующих элементов -й строки, а один из элементов -й строки больше соответствующего элемента -й строки, то стратегия доминирует над стратегией , и поэтому стратегия несущественна и может быть исключена из платежной матрицы. Подобные рассуждения могут быть проведены в отношении столбцов. Кроме того, в платежной матрице могут существовать одинаковые строки и одинаковые столбцы, то есть дублирующие стратегии. Из нескольких дублирующих стратегий нужно оставлять одну.

Практическая работа № 8

Задача

Выявить существенные стратегии для платежной матрицы.

.

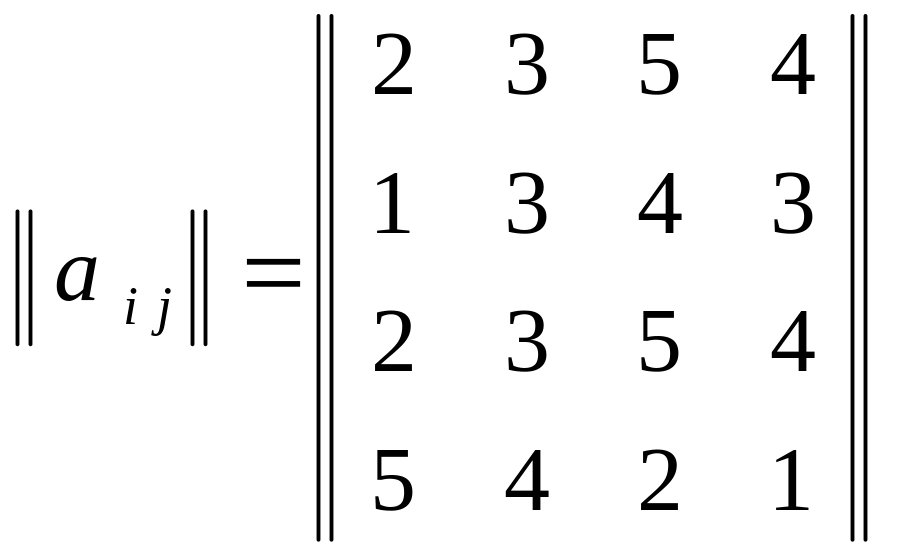Решение

Стратегии и — дублирующие, кроме того, стратегия доминирует над стратегией . Поэтому существенные стратегии системы имеют вид

.

В полученной матрице стратегия доминирует над стратегией , которую считаем несущественной. Окончательно платежная матрица примет вид

.

В теории игр имеет место следующая теорема. У любой конечной игры имеется решение, в котором число существенных стратегий каждой системы не превосходит наименьшего из чисел и . Справедливы следующие свойства оптимальных стратегий матричной игры.

Если система использует -ю существенную стратегию, а система – оптимальную смешанную стратегию , то выигрыш системы равен цене игры, то есть

. (8.1)

Если система использует -ю существенную стратегию, а система – оптимальную смешанную стратегию , то проигрыш системы равен цене игры, то есть

. (8.2)

На основе свойств оптимальных стратегий легко решить игру , заданную платежной матрицей

.

Пусть известно, что игра не имеет седловой точки. Так как все стратегии в игре существенные, на основании формул (8.1) и (8.2) с учетом условия (11.5) можно записать системы уравнений

решение которых относительно и представляет собой решение игры:

(8.3)

Решению игры можно дать удобную геометрическую интерпретацию (рис.8.1).

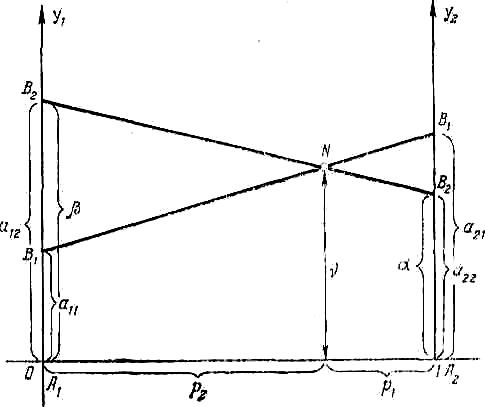
Рис. 8.1. Геометрическая интерпретация решения игры

Возьмем отрезок оси абсцисс единичной длины. Левый конец отрезка изображает стратегию , правый конец – стратегию ; внутренние точки отрезка представляют смешанные стратегии системы . Вероятность стратегии равна расстоянию от точки до правого конца отрезка, а вероятность стратегии – расстоянию от точки до левого конца отрезка. В точках и восстановим два перпендикуляра к оси абсцисс и . На оси будем откладывать выигрыш при чистой стратегии , а на оси – выигрыш при чистой стратегии . Если система применяет стратегию , то выигрыш стороны при стратегии будет , при стратегии – . Точку с ординатой на оси и точку с ординатой на оси соединим прямой. Любая смешанная стратегия системы даст выигрыш, равный ординате точки на отрезке , исключая его концы.

Аналогично строится прямая . Так как система стремится минимизировать свой проигрыш, то нижней границей выигрыша системы будет ломаная линия .

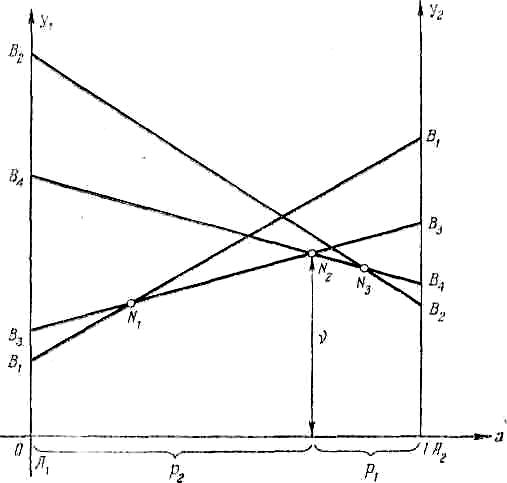
Рис. 8.2. Геометрический способ решения игры

Стремясь максимизировать свой минимальный выигрыш, система выберет оптимальную стратегию , соответствующую точке , как имеющую наибольшую ординату на ломаной . Эта ордината представляет собой цену игры , а точка ее пересечения с осью абсцисс делит отрезок в отношении . Для определения оптимальной стратегии системы строится график в стратегиях , , на котором ищут минимум верхней границы проигрыша системы .

На основании теоремы о существенных стратегиях игры и могут быть сведены к игре , так как число существенных стратегий каждой системы равно двум. Геометрический способ решения игры показан на рис. 8.2.

На графике строятся линии стратегий . Для определения существенных стратегий системы среди точек пересечения линий ее стратегий выбирается точка , имеющая максимальную ординату. Точка определяет существенные стратегии системы (в данном случае это стратегии и ), а ордината точки представляет собой цену игры . Таким образом, игра сведена к игре , которая решается элементарно. Решение игры проводится аналогично, с той разницей, что строится верхняя граница проигрыша, на которой ищут минимум.

Практическая работа № 9

Задача

Система имеет три типа танкового вооружения , , ; система имеет три типа противотанкового вооружения: , , .

Задана платежная матрица:

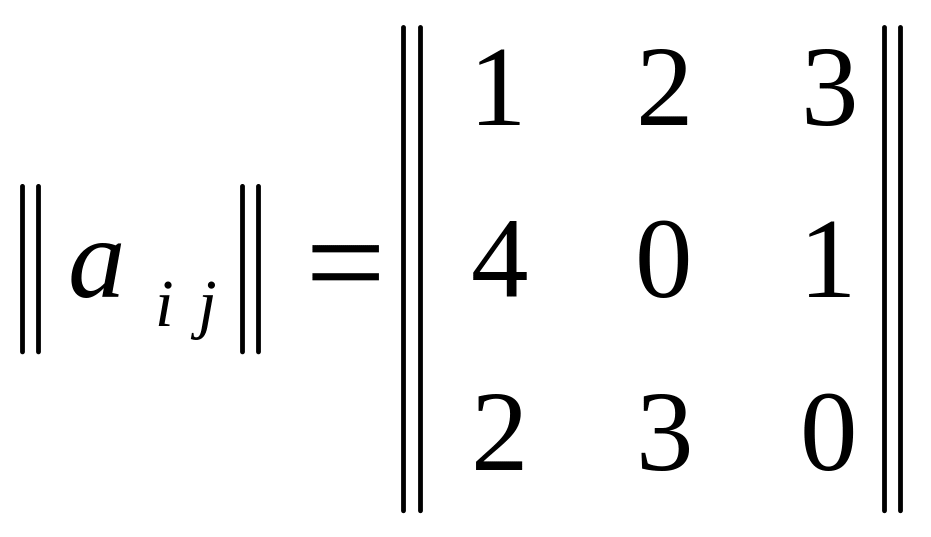
Определить оптимальные соотношения типов танкового и противотанкового вооружения для каждой системы.

Решение. Составим пару двойственных задач линейного программирования:

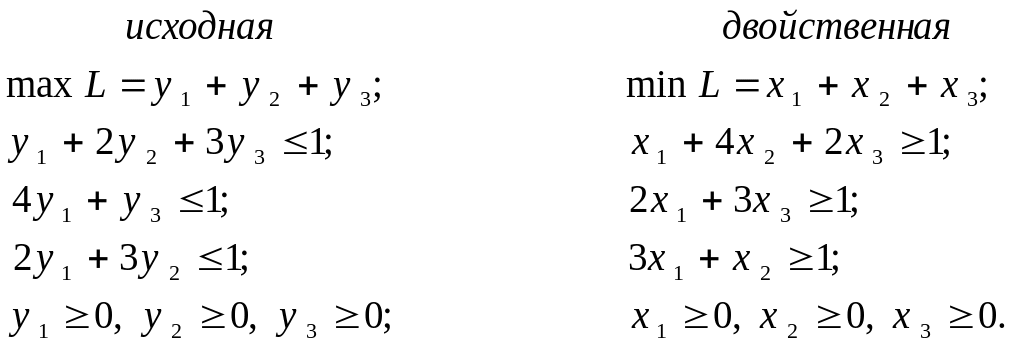
Оптимальные решения этих задач соответственно

Найдем цену игры:

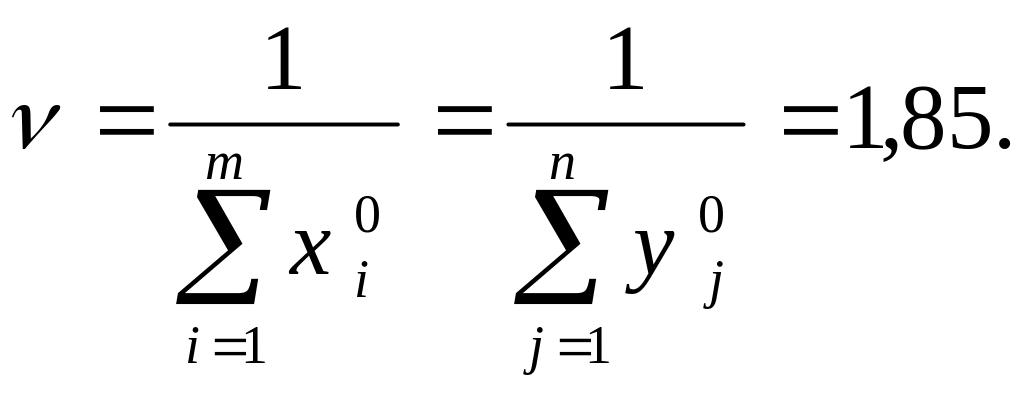
Составляющие оптимальных стратегий, определяющие оптимальное соотношение видов вооружения для обеих систем, находятся по формулам:

; .

Возможность сведения игровой задачи к паре двойственных задач линейного программирования существенно расширяет область применения теории игр в сфере управления сложными военно-техническими системами. Если ранее игра рассматривалась как состязание двух систем, преследующих противоположные цели, то, благодаря идее двойственности, принятие оптимального решения системой может рассматриваться как игровая задача. Целесообразность такого подхода основывается на следующих рассуждениях.

Принятие оптимального решения по модели линейного программирования сводится к задаче оптимального распределения ограниченных ресурсов. Тогда система, принимающая решение, может быть разделена на две подсистемы:

- подсистему планирования (решает исходную задачу);

- подсистему, формирующую ресурсы (решает двойственную задачу).

Задача оптимального планирования состоит в выборе таких переменных, которые при заданных ресурсах максимизируют эффект, формально определенный в виде целевой функции. С другой стороны, необходимо выбрать такие характеристики ресурсов, чтобы суммарные затраты на их приобретение были минимальными, но обеспечивали заданное значение целевой функции. Совместное решение этих задач с точки зрения математики может быть рассмотрено как игра между подсистемами планирования и формирования ресурсов.

Дадим двойственным задачам следующую военно-техническую трактовку. Требуется производить типов вооружения, каждый в количестве . Эффективность единицы -го типа вооружения задана коэффициентами . Для достижения требуемого эффекта необходимо ресурсов, причем -й ресурс выделен в количестве . Расход ресурса -го типа на производство единицы вооружения -го типа задан в виде элемента матрицы ограничений. Подсистема планирования определяет оптимальный план производства вооружения, то есть такие количества единиц вооружения , которые максимизируют суммарный эффект их использования при заданных величинах ресурсов .

Подсистема формирования ресурсов решает задачу оптимального выбора видов ресурсов из имеющихся в наличии. Если имеются несколько видов одного и того же ресурса, то для их характеристики вводится двойственная переменная , называемая удельной оценкой ресурса. Физически двойственная переменная означает влияние ресурса -го типа на эффективность единицы вооружения -го типа. Подсистема формирования ресурсов будет выбирать такие оптимальные виды ресурсов, которые обеспечивали бы эффективность единицы вооружения, удовлетворяющие ограничениям задачи, и минимизировали ее целевую функцию.

Так как оптимальные значения целевых функций исходной и двойственной задач равны, то их совместное решение определяет оптимальное распределение оптимально выбранных ресурсов.

Для решения матричных игр американским ученым Г. Брауном предложен приближенный метод. Идея метода заключается в моделировании способов поведения систем в конфликтной ситуации. Рассмотрим сущность метода на примере решения игры, заданной игровой матрицей

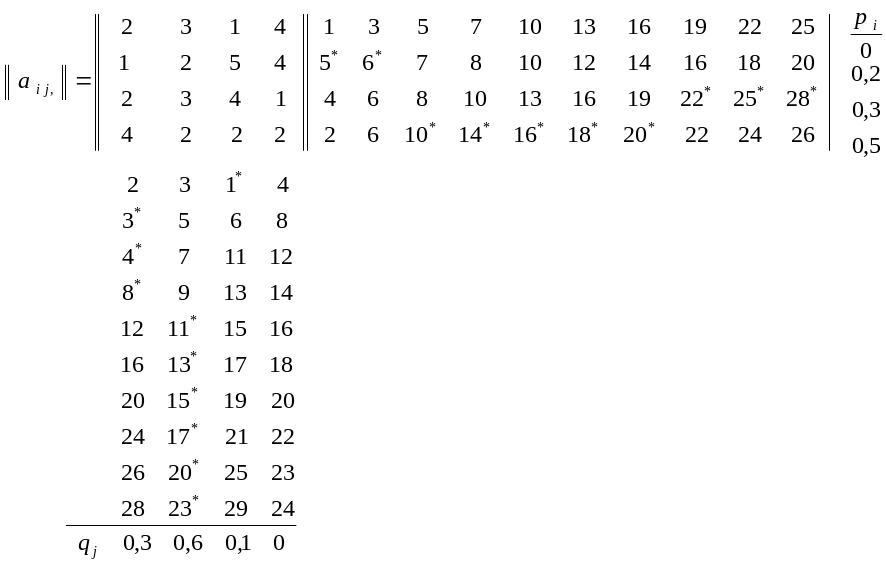
Решение игры методом Брауна начинается со случайного выбора стратегии одной из систем. Пусть система выбрала стратегию . Выпишем элементы этой стратегии под игровой матрицей. Система , минимизируя свой проигрыш, выберет стратегию , соответствующую минимальному элементу стратегии . Выпишем элементы стратегии справа от матрицы. Система находит среди элементов стратегии максимальный элемент и выбирает стратегию , соответствующую максимальному выигрышу. Элементы стратегии прибавляются к элементам стратегии и записываются под матрицей.

Аналогичные итерации повторяются столько раз, сколько необходимо для решения игры с требуемой точностью. В приведенном примере выполнено 10 итераций, причем на каждой итерации максимальный выигрыш системы и минимальный проигрыш системы отмечаются звездочкой.

Подсчитав число отмеченных элементов в каждой стратегии сторон, получим частоту использования каждой стратегии путем деления числа отмеченных элементов стратегии на общее число итераций. При достаточно большом числе итераций частоты стратегий сводятся к вероятностям, которые и являются оптимальными решениями матричной игры.

За 10 проведенных итераций получены оптимальные стратегии:

; .

В методе Брауна точность полученного решения повышается при увеличении числа итераций.

Так как матричная игра соответствует паре двойственных задач линейного программирования, то метод Брауна можно использовать для решения этих задач.

Особенно перспективно использование метода Брауна для получения приближенного решения в больших задачах линейного программирования, а оптимальное решение лучше искать симплексным методом.