Розділ 3. Результати
3.1 Результат роботи програми
Щоб оцінити роботу програми, вирішимо чисельно, а також за допомогою точної формули конкретну задачу.
Розглянемо падіння сталевої кульки (щільності 7800 кг / м 3 і радіуса 1 см) в гліцерині (щільність 1261 кг / м 3, в'язкість при температурі 20 о С - 1.49 Па * с), в момент часу t 0 = 0 (тіло знаходиться у спокої на початку координат). Знайдемо його координати в момент часу 1секунда після початку руху.
Задамо для методу Рунге-Кутти інтервал часу, рівний однієї десятитисячної секунди (0,0001 с).
Значення, отримане методом Рунге-Кутти, складає 0,845197 м, а точне значення - 0,845149 м. Різниця між цими величинами складає 0,000048 - всього 0,057%.
Для наочності розглянемо графіки значень координат при значно меншому числі кроків (і відповідно, меншою точності). Нехай інтервал часу буде дорівнювати 0,05 с.
Рис. 1 Графік координат при меншому числі кроків
Значення координат, отриманих для моменту часу 1сек при цьому інтервалі (і, отже, 20 кроках), складає 0,818847 м. Різниця з точним значенням становить 0,021508, тобто 2,54%.
Р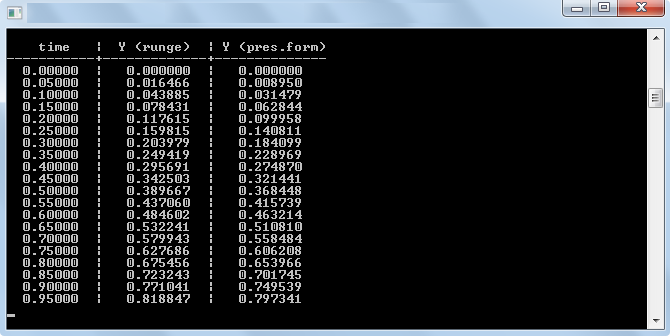
езультат
роботи програми з такими параметрами:
Рис. 2 Результат роботи програми
Цікаво відзначити, що навіть при такому грубому наближенні рішення для швидкості виявляється на кілька порядків точніше. Так, з удвічі меншим інтервалом (0,025 с) в момент часу 0,5 с (тобто також після 20 кроків) значення, отримане чисельними методами, виходить рівним 0,943383 м / c , а точне значення - 0,953384 м / c і відрізняється всього на 0,000001 м / с або близько 0,0001%.
Причина цієї розбіжності в точності для координати і швидкості полягає в тому, що задача Коші:
у разі швидкості зводилася до рівняння
тобто похідна швидкості не залежала явно від часу, а залежала тільки від значення самої швидкості. У той же час для координат ми мали диференціальне рівняння
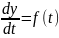
тобто в правій частині ми, чисельно розв'язуючи задачу, могли отримати лише залежність від часу. Явної залежності від координати тут не було.
Таким чином, різниця в точності рішення обох рівнянь пояснюється відмінністю їх правих частин, а саме - від яких параметрів ці праві частини залежать.
Висновки
У цій роботі було вивчено рух твердого тіла у в'язкій рідини, складено рівняння руху і знайдені точні вирази для швидкості і координат тіла. Був також вивчений і застосований для чисельного рішення диференціального рівняння метод Рунге-Кутти.
Чисельний метод застосовувався для вирішення завдання в два етапи - спочатку було вирішено диференціальне рівняння для швидкості (при цьому в рівнянні похідна явно залежала тільки від швидкості, і не залежала від часу), потім було записано диференціальне рівняння, що зв'язує поняття координати і швидкості , знаючи значення швидкості в потрібні моменти часу, знову вирішено чисельними методами (у цьому випадку похідна виходила функцією тільки від часу, і явно не залежала від координати).
Отримані чисельні рішення для швидкості виявилися дуже добре відповідними точним рішенням навіть при невеликій кількості кроків (з швидко спадної практично до нуля похибкою).
Рішення ж для координати при малому числі кроків відрізнялися від точних рішень на значення порядку декількох відсотків, однак зі збільшенням числа кроків похибка помітно знизилася - аж до сотих часток відсотка при 10.000 кроків.
Метод Рунге-Кутти показав себе як дуже точний і простий в реалізації у задачі для рішення диференціальних рівнянь.