Розділ 1

1. Рух тіла у в'язкому середовищі

Розглянемо занурене у в'язку рідину тверде тіло (для простоти – кулькообразної форми). На це тіло діють наступні сили:

сила земного тяжіння

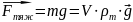
сила Архімеда з боку рідини

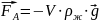
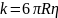і сила внутрішнього тертя, яка при досить малих швидкостях руху виявляється прямо пропорційна швидкості і спрямована протилежно напрямку руху. При цьому коефіцієнт опору середовища k прямо пропорційний в'язкості середовища і площі дотику тіла і рідини. Для тіл сферичної форми радіуса R він буде дорівнює  . Таким чином, сила внутрішнього тертя дорівнює:

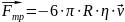
Рівнодіюча цих сил буде дорівнювати:

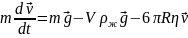
Рух буде рівномірним, тому, якщо направити вісь OY вертикально вниз, то в проекції на цю вісь рівняння матиме вигляд:

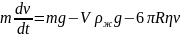
Можна привести його до вигляду задачі Коші:

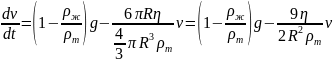
з початковими умовами 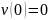 , 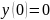. Вважаючи праву частину рівняння рівним f (y, v), можна розв’язати його чисельними методами, що й було зроблено в даній роботі. Крім того, можна знайти точне рішення рівняння, щоб перевірити точність методу Рунге-Кутти. 

Якщо ввести позначення

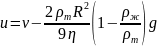
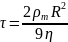
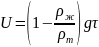
рівняння можна записати у вигляді

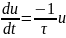
або

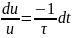
Проінтегрувавши, отримуємо

Або

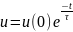
Враховуючи, що 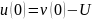 , рівняння записується у вигляді

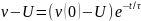
Оскільки в початковий момент часу швидкість тіла дорівнює нулю, то остаточно для швидкості отримуємо рівняння:

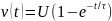
Проінтегрувавши даний вираз за часом і враховуючи, що в початковий момент тіло перебувало на початку координат 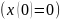, знаходимо вираз для залежності координати тіла від часу:

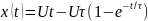
2. В'язкість (внутрішнє тертя) і в'язкопружність

У фізичної моделі ідеальної рідини передбачається, що в рідкому середовищі відсутнє внутрішнє тертя, тобто взаємодія між елементами середовища, спрямована уздовж поверхні їхнього зіткнення. Однак, у реальній рідині така взаємодія присутня, і така властивість називається в'язкістю. В'язкість обумовлена ​​тим, що дотичні шари рідини, що рухаються з різними швидкостями, за рахунок дифузії обмінюються молекулами, а як наслідок - імпульсом. Шар, що рухається з більшою швидкістю, втрачає частину своїх швидких молекул, і натомість отримує повільні молекули, а шар, що рухається з меншою швидкістю, навпаки - втрачає повільні і отримує швидкі молекули. За рахунок цього швидкість руху першого шару знижується, а швидкість руху другого - зростає.

Властивість в'язкопружності деяких рідин означає, що вони можуть вести себе і як пружні тіла, і як в'язкі рідини. При цьому якщо з боку зовнішнього середовища на них виробляється вплив, протягом досить короткого часу, то рідина веде себе, як пружне тверде тіло, і тільки через деякий час після початку дії починає рухатися, як в'язка рідина.

2. Актуальність данної роботи

Існуючі рішення

При описі руху тіла у в'язкому середовищі виникають диференціальні рівняння, які в найпростіших випадках можуть бути вирішені якісно із знаходженням точних формул, що описують рух, проте в більш складних ситуаціях (при обліку в моделі додаткових факторів) це виявляється не завжди можливо і тоді доводиться використовувати методи чисельного вирішення цих диференціальних рівнянь.

Виникає рівняння виду

 

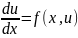
з початковою умовою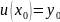

називається задачею Коші. При чисельному рішенні необхідно знайти значення функції 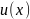  в заданій точці. При цьому послідовно шукається значення в точках множини x_n, (n = 1, ... N), де x_n як правило і є потрібна нам точка.

Найпростіший з таких методів це метод Ейлера. У ньому весь відрізок від x₀ до x_n  розбивається на рівні відрізки довжини h, і наближено покладається, що

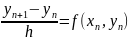
звідки по рекурентного співвідношення

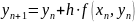
знаходиться значення y_n функції u у всіх точках аж до x_n.

Однак, метод Ейлера є досить приблизним і має малу точність. Існують модифікації цього методу, названі виправленим методом Ейлера і модифікованим методом Ейлера. Вони мають більш високу точність, проте існує сімейство ще більш точних методів, так званих методами Рунге-Кутти. При цьому згадані три методи виявляються частими випадками методу Рунге-Кутти.

Так, метод Ейлера являє собою метод Рунге-Кутти першого порядку, а його модифікації - методами Рунге-Кутти другого порядку. У даній роботі використовується найпоширеніший з представників цього сімейства, який є методом Рунге-Кутти четвертого порядку (одним з багатьох) і називається просто методом Рунге-Кутти. Він є, з одного боку, досить простим в реалізації, в порівнянні з аналогічними більш високого порядку, з іншого боку - має хорошу точність, достатню для більшості випадків.