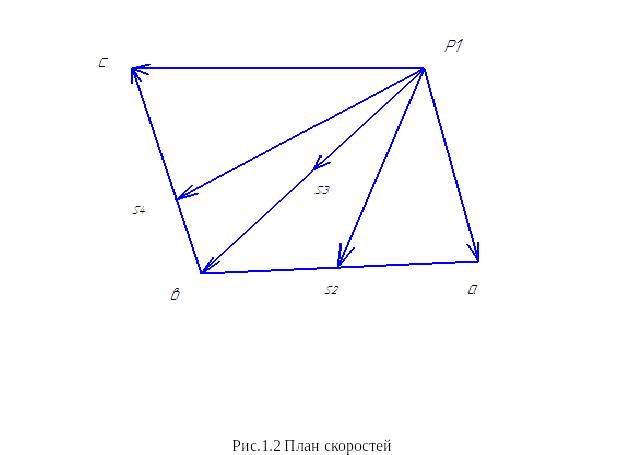
2. Построение планов скоростей.

В масштабе _v строим 12 планов скоростей.

где V_А – линейная скорость т. А;

₁ – частота вращения звена ОА, ;

₁= ;

l_ОА – истинная длина звена ОА в м.

Определяем масштаб плана скоростей:

_V =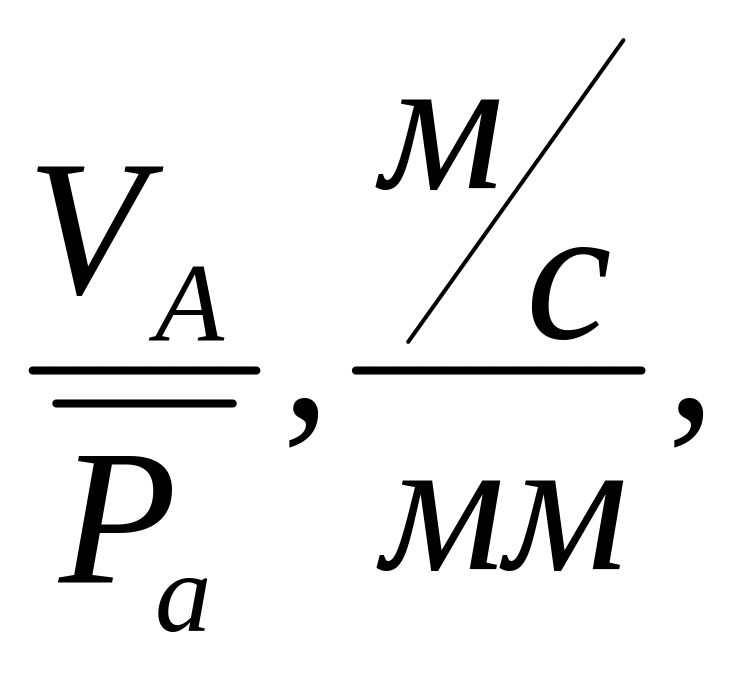

- отрезок в мм на плане скоростей, характеризующий истинную скорость точки А. Выбирается произвольно. Примем =40 мм, тогда

_V = .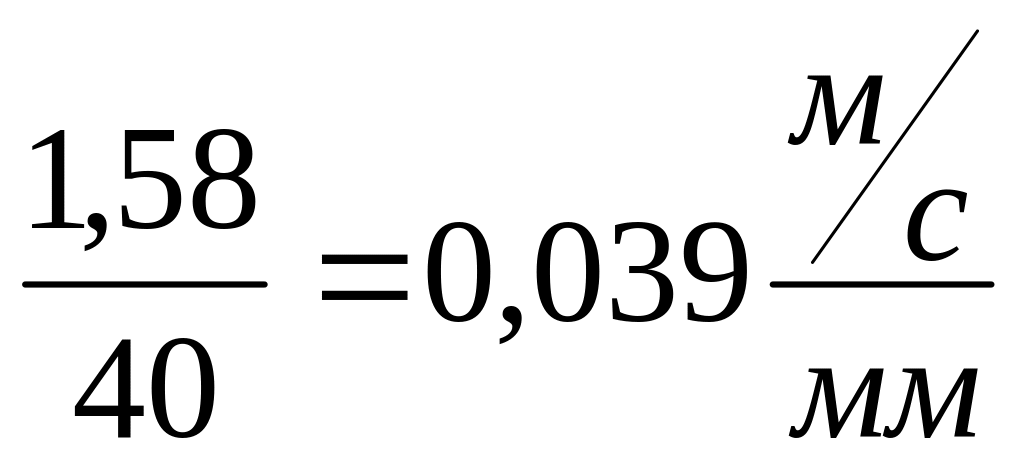

т. Р – полюс плана скоростей.

где - вектор линейной скорости точки В. Направлен перпендикулярно к звену ВС в сторону вращения этого звена;

- вектор линейной скорости точки А. Направлен перпендикулярно к звену ОА в сторону вращения этого звена;

- вектор скорости точки В в относительном вращательном движении вокруг точки А. Известен только по направлению и перпендикулярен звену АВ.

- вектор линейной скорости точки С. Направлен по ходу ползуна;

Для построения плана скоростей из точки Р1 проводим =40 мм перпендикулярно звену ОА. Из точки Р1 проводим линию, перпендикулярную звену ВО₃ в сторону вращения этого звена. Из конца вектора перпендикулярно звену АВ проводим линию до пересечения ее с линией, перпендикулярной звену ВО₃. Точка пересечения этих линий – точка b. Таким образом, направления векторов и совпадают с направлением движения звеньев ОА и ВО₃ соответственно, начало вектора находится в конце вектора , конец – в конце вектора .

Для нахождения точки с на плане скоростей из полюса проводим вектор, совпадающий с направлением скорости точки С (вертикально вверх или вертикально вниз по ходу ползуна). На пересечении этих векторов и находится точка с.(рис1.2)

Построив таким же образом остальные планы скоростей, найдем истинные значения скоростей V_B, V_BA, V_С, V_СВ, по формулам:

где , - отрезки в мм на плане скоростей;

_V – масштаб плана скоростей.

Определяем линейную скорость точки В для 1-ого положения:

где - отрезок в мм на плане скоростей;

_V – масштаб плана скоростей.

Подставляя соответствующие значения для остальных положений в формулу нахождения линейной скорости точки В получим:

Определяем истинную скорость точки В в относительном вращательном движении вокруг точки А.

где - отрезок в мм на плане скоростей;

_V – масштаб плана скоростей.

Подставляя соответствующие значения для остальных рабочих положений в формулу нахождения линейной скорости точки В в относительном вращательном движении вокруг точки А, получим:

Определяем истинную скорость точки С в относительном вращательном движении вокруг точки В.

где - отрезок в мм на плане скоростей;

_V – масштаб плана скоростей.

Подставляя соответствующие значения cb для остальных рабочих положений в формулу нахождения линейной скорости точки C в относительном вращательном движении вокруг точки B, получим:

Определяем истинное значение линейной скорости точки С:

где - отрезок в мм на плане скоростей;

_V – масштаб плана скоростей.

Подставляя соответствующие значения для остальных положений в формулу нахождения линейной скорости точки С, получим:

Определяем скорости центров масс звена АВ

где - отрезок в мм на плане скоростей;

_V – масштаб плана скоростей.

Подставляя соответствующие значения для остальных положений в формулу нахождения линейной скорости точки S₂, получим:

Определяем скорости центров масс звена О₃В

где - отрезок в мм на плане скоростей;

_V – масштаб плана скоростей.

Подставляя соответствующие значения для остальных положений в формулу нахождения линейной скорости точки S₃, получим:

Определяем скорости центров масс звена ВС

где - отрезок в мм на плане скоростей;

_V – масштаб плана скоростей.

Подставляя соответствующие значения для остальных положений в формулу нахождения линейной скорости точки S₄, получим:

Также находим угловые скорости звена АВ для каждого положения:

где V_BA – истинное значение скорости т. В в относительном вращательном движении вокруг точки А;

l_АВ – истинная длина звена АВ в м.

Подставляя в данную формулу соответствующие для каждого положения значения V_BA, получим:

Находим угловые скорости звена О₃В для каждого положения:

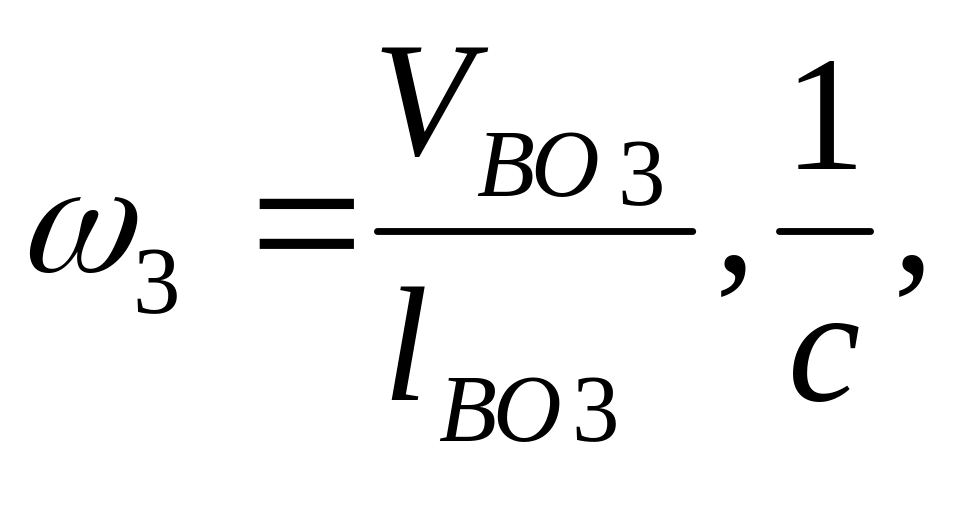
где V_BО3 – истинное значение скорости т. В в относительном вращательном движении вокруг точки О₃;

l_ВО3 – истинная длина звена ВО3 в м.

Подставляя в данную формулу соответствующие для каждого положения значения V_BО3, получим:

Находим угловые скорости звена СВ для каждого положения:

где V_СВ - скорость точки В в относительном вращательном движении вокруг точки C;

l_ВC = 410 мм =0,41 м.

Подставляя в данную формулу соответствующие для каждого положения значения V_CВ, получим:

Результаты расчетов заносим в таблицу 1.1.

Таблица 1.1.

Линейные и угловые скорости механизма.

Параметры Полож. мех.	VA,м/с	VB,м/с	VBА,м/с	VCВ,м/с	VС,м/с	VS2	VS3	VS4	ВА, м/с	ВО3, м/с	CВ, м/с
0, 12	1,58	2,02	1,4	2,04	0	1,71	0	1,28	7	9,2	4
1	1,58	2,22	1,87	1,67	1,95	171	1,13	1,95	9,35	10,57	4,07
2	1,58	2,14	2,1	0,15	2,26	1,56	1,09	2,22	10,5	10,19	0,36
3	1,58	1,59	2,03	0,89	1,01	1,24	0,81	1,32	10,15	9,04	2,17
4	1,58	1,32	1,75	1,09	0,46	1,17	0,66	0,89	8,75	6,28	2,65
5	1,58	1,09	1,4	1,05	0,15	1,13	0,58	0,7	7	5,19	2,56
6	1,58	1,05	1,44	1,01	0,12	1,13	0,54	0,66	7,2	5	2,46
7	1,58	1,17	1,24	0,93	0,39	1,24	0,58	0,81	6,2	5,57	2,26
8	1,58	1,2	1,09	0,7	1,7	1,28	0,58	0,97	5,45	5,71	1,7
9	1,58	1,44	0,97	0,27	1,28	1,44	0,78	1,4	4,85	6,85	0,65
10	1,58	1,56	0,93	0,62	1,75	1,44	0,78	1,56	4,65	7,42	1,51
11	1,58	1,59	1,17	1,56	1,4	1,56	0,89	1,48	5,85	7,57	3,8

1.3 Построение плана ускорений для заданного (7-го) положения механизма.

Т. к. угловая скорость звена ОА ₁=const, то ускорение точки А определим по формуле:

где l_ОА – истинная длина звена ОА;

₁ - угловая скорость звена ОА.

Из полюса  плана ускорений отложим отрезок произвольной длины а параллельно звену ОА от точки А к точке О. Примем а = 100 мм, тогда масштаб плана ускорений:

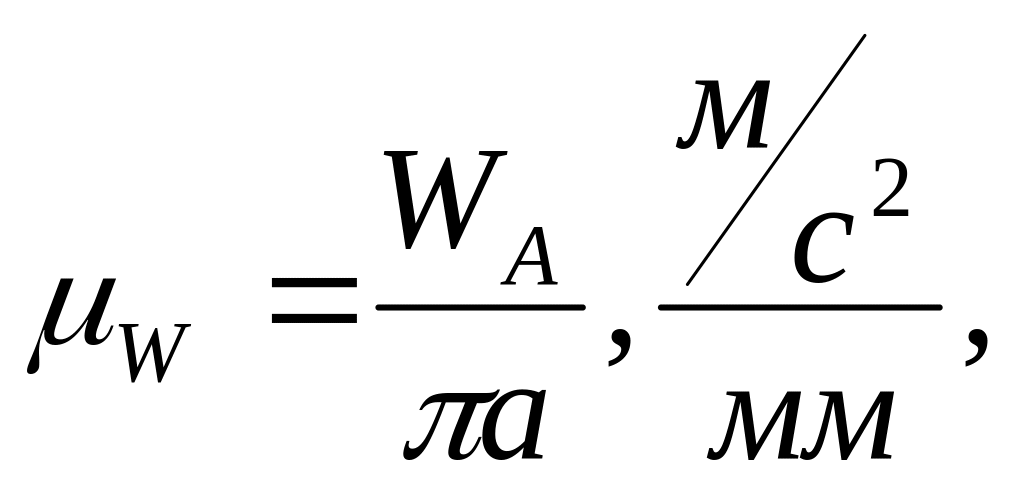
где - ускорение точки А;

а – отрезок в мм на плане ускорений, изображающий истинное ускорение точки А.

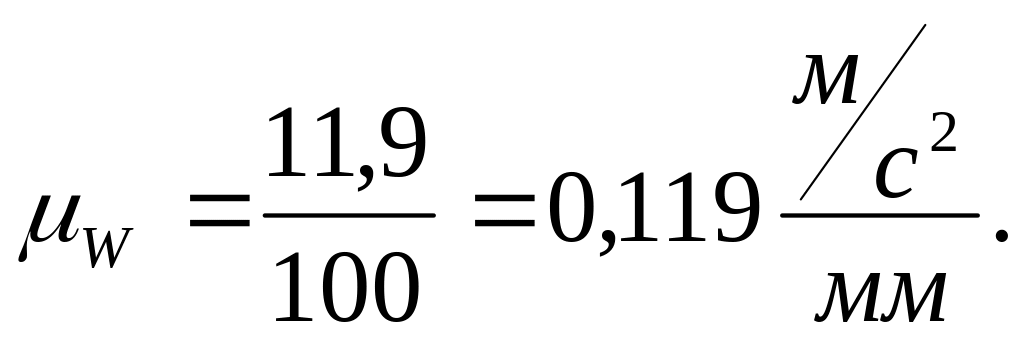
Для определения ускорения точки В используем следующие векторные уравнения:

где - вектор абсолютного ускорения точки В;

- вектор нормального ускорения точки В в относительном вращательном движении вокруг точки А. Направлен параллельно звену ВА от В к А;

- вектор тангенциального ускорения точки В в относительном вращательном движении вокруг точки А. Направлен перпендикулярно звену ВА.

где - вектор нормального ускорения точки В в относительном вращательном движении вокруг точки О3. Направлен параллельно звену ВО3 от В к О3;

- вектор тангенциального ускорения точки В в относительном вращательном движении вокруг точки О3. Направлен перпендикулярно звену ВО3;

- вектор абсолютного ускорения точки C. Равный по модулю вектору .

Величину нормального ускорения определяем по формуле:

где l_ВА - истинная длина звена ВА (в 7-м положении);

Чертежное значение , изображающее ускорение на плане ускорений в масштабе _W, определяем по формуле:

где - вектор нормального ускорения точки В в относительном вращательном движении вокруг точки А;

- масштаб плана ускорений.

Величину нормального ускорения определяем по формуле:

где l_ВО3 - истинная длина звена ВО3 (в 7-м положении);

Чертежное значение , изображающее ускорение на плане ускорений в масштабе _W, определяем по формуле:

где - вектор нормального ускорения точки В в относительном вращательном движении вокруг точки О3;

- масштаб плана ускорений.

Для определения ускорения точки С используем следующее векторное уравнение:

где - вектор абсолютного ускорения точки С;

- вектор нормального ускорения точки В в относительном вращательном движении вокруг точки C. Направлен параллельно звену ВC от С к В;

- вектор тангенциального ускорения точки В в относительном вращательном движении вокруг точки C. Направлен перпендикулярно звену CВ.

Величину нормального ускорения определяем по формуле:

где l_CВ - истинная длина звена CВ (в 7-м положении);

Чертежное значение , изображающее ускорение на плане ускорений в масштабе _W, определяем по формуле:

где - вектор нормального ускорения точки В в относительном вращательном движении вокруг точки C;

- масштаб плана ускорений.

Построение ведем в такой последовательности (рис. 1.3).

После построения , из конца этого вектора проводим вектор , изображающий ускорение на плане ускорений. Из конца этого вектора проводим отрезок произвольной длины перпендикулярно звену АВ. Из полюса  плана ускорений проводим вектор , изображающий ускорение на плане ускорений. Из конца этого вектора перпендикулярно звену ВО3 проводим отрезок до пересечения его с отрезком, проведенным перпендикулярно звену АВ. Точка их пересечения – точка B. Соединив полюс  с точкой , получим вектор , характеризующий абсолютное ускорение точки В (W_B) на плане ускорений. Соединив конец вектора с точкой , получим вектор , изображающий ускорение на плане ускорений, конец вектора с точкой , - вектор , изображающий ускорение на плане ускорений. Соединив а и в - получим вектор , характеризующий ускорение точки В в относительном вращательном движении вокруг точки А. Из точки в проводим вектор параллельно звену СВ, который характеризует нормальное ускорение звена CВ. Из конца этого вектора проводим отрезок, перпендикулярный звену СВ до пересечения с вертикальной линией, проходящей через полюс . Этот отрезок характеризует тангенциальное ускорение звена CВ. Соединив полюс с концом последнего отрезка, получим полное ускорение т.С, направленное параллельно оси оу вверх.

Определение тангенциального ускорения точки В относительно точки А

,

где - отрезок в мм на плане ускорений

μ_W - масштаб плана ускорений

Определение полного ускорения точки В.

,

где - отрезок в мм на плане ускорений

μ_W - масштаб плана ускорений

Определение тангенциального ускорения точки С относительно точки В

,

где - отрезок в мм на плане ускорений

μ_W - масштаб плана ускорений

Определение полного ускорения точки С.

,

где - отрезок в мм на плане ускорений

μ_W - масштаб плана ускорений

Определение угловых ускорений.

Угловое ускорение звена АВ определяется по формуле:

Угловое ускорение звена ВC определяется по формуле:

Полученные данные заносим в таблицу 1.2

Таблица 1.2

Линейные и угловые ускорения т.D

Параметр Полож. мех.	WA м/с2	W м/с2	W м/с2	W м/с2	WB м/с2	W м/с2	W м/с2	WC м/с2	ВА, 1/c2	СВ, 1/c2
3	11,9	20,56	12,17	2,13	14,04	5,47	6,66	13,56	27,35	16,24
4	11,9	15,4	11,01	3,33	6,3	0,357	4,76	7,97	1,785	11,6
7	11,9	7,78	6,09	2,31	11,06	2,38	1,78	4,16	11,9	4,34
10	11,9	4,75	11,01	0,94	11,42	0	12,73	4,52	0	31,04

1.4 Построение диаграммы зависимости перемещения ползуна от угла поворота ведущего звена S=S().

Для построения диаграммы на оси абсцисс откладываем отрезок l_0-12, (рис.1.4,а). Масштаб оси абсцисс _ определяется по формуле:

_=

где l_0-12 – отрезок в мм. на диаграмме, характеризующий один полный оборот кривошипа. Примем l_0-12 =240 мм, тогда

_=

Для нахождения масштаба времени используем формулу:

_t=

где _ - масштаб оси абсцисс данной диаграммы;

₁ – угловая скорость звена ОА.

_t=

Вдоль оси ординат откладываем перемещение ползуна С, опираясь на кинематическую схему механизма, начиная с нулевого положения. Каждый из 12-ти отрезков, на которые разбита ось абсцисс, соответствует определенному положению механизма. В первом положении перемещение ползуна С равно 0, следовательно, 0-ой точке на диаграмме будет соответствовать нулевое перемещение. На следующем (1-м) отрезке откладываем расстояние (в определенном масштабе),

Sd

5` 6`

4` 7`

3` 8`

9`

2`

10`

1` 11`

0 1 2 3 4 5 6 7 8 9 10 11 12

Рис. 1.4 (а). Диаграмма зависимости перемещения ползуна от угла поворота ведущего звена

Vd

2``

3``

4``

1`` 5``

6`` 6 7 8 9 10 11 12

0 1 2 3 4 5

7`` 12``

8``

^H1

9`` 10`` 11``

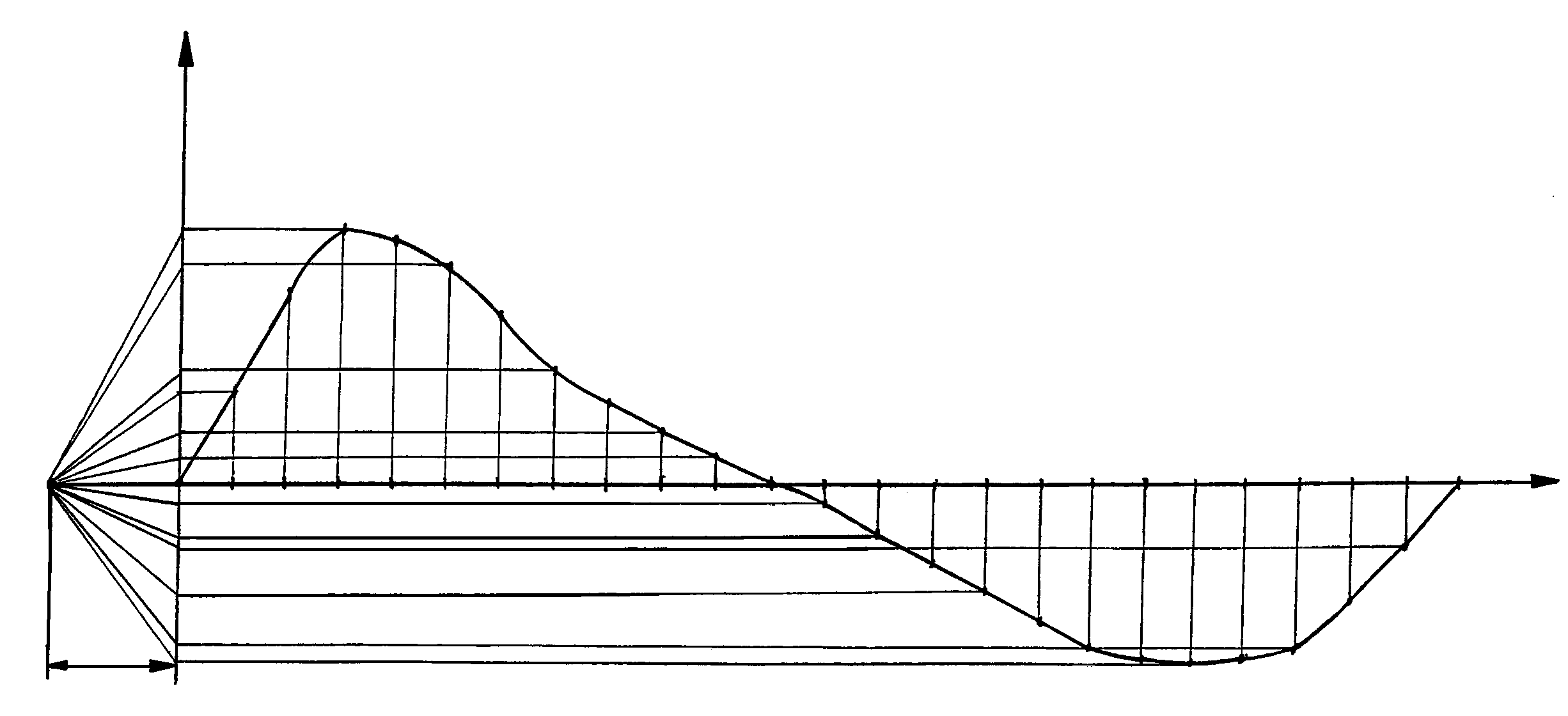
Рис. 1.4 (б). Диаграмма зависимости скорости ползуна от угла поворота ведущего звена

Wd

1”’ 1”’

12”’

11”’

2”’2 3 4 5 6 7 8 9

P2 0 1 10”’10 11 12 1

5”’ 6”’ 9”’

3”’ 4”’ 7”’ 8”’

H2

Рис. 1.4 (в). Диаграмма зависимости ускорения ползуна от угла поворота ведущего звена

которое соответствует перемещению ползуна из 0-го в 1-ое положение (отрезку С₀С₁ из кинематической схемы механизма). На 2-м отрезке (в том же масштабе) откладываем расстояние, которое соответствует перемещению ползуна из 0-го во 2-ое положение (отрезку С₀С₂). Таким же образом откладываем остальные расстояния вдоль оси ординат на диаграмме, заканчивая 12-м положением, которое характеризуется 0-м перемещением ползуна (т. е. ордината равна 0). Полученные точки соединяем и получаем кривую расстояний точки С от нулевого крайнего положения (нумеруем эти точки 1’,2’,3’) и т. д.

Определяем масштаб оси ординат данной диаграммы по формуле:

_S=

где – расстояние на кинематической схеме механизма, соответствующее перемещению ползуна С из 0-го в i-тое положение (например, в 10-ом), тогда С₀С₁₀=60 мм;

- расстояние вдоль оси ординат на диаграмме перемещения т. С, соответствующее i-тому отрезку (в данном случае отрезку 10), =30 мм;

_l - масштаб построения кинематической схемы механизма.

_S=

1.5 Построение диаграммы зависимости скорости ползуна С от угла поворота ведущего звена V=V().

Построение осуществляем графическим дифференцированием диаграммы перемещения (с помощью метода хорд). Для построения данной диаграммы на оси абсцисс откладываем отрезок l_0-12 =240 мм и разбиваем его на 12 равных частей, по величине равных отрезкам с диаграммы перемещения ползуна С (рис. 1.4,б). На этой же оси откладываем влево от оси ординат расстояние Н₁ – полюсное расстояние в мм. Выбирается произвольно. Получаем точку Р₁ (примем Н₁=43,35 мм).

На диаграмме перемещения точки С проводим прямые линии, соединяющие точки 01’, 1’2’, 2’3, и т. д. На диаграмме скорости точки С делим построенные по оси абсцисс отрезки на равные части. Далее для каждого рабочего положения осуществляем следующие действия: из точки Р₁ на графике скорости проводим линию, параллельную линии 01’, до пересечения ее с осью ординат. Из полученной точки пересечения на оси ординат проводим отрезок, параллельный оси абсцисс до середины участка 01. Конец этого отрезка - точка 1’’.

Аналогичным образом осуществляем действия для всех рабочих положений и получаем точки 2’’,3’’,4’’ и т. д. Соединив полученные точки, получим диаграмму скорости точки С. Точкам 0 и 12 на оси абсцисс должна соответствовать 0-ая ордината.

Масштаб оси ординат диаграммы скорости точки С определяем по формуле:

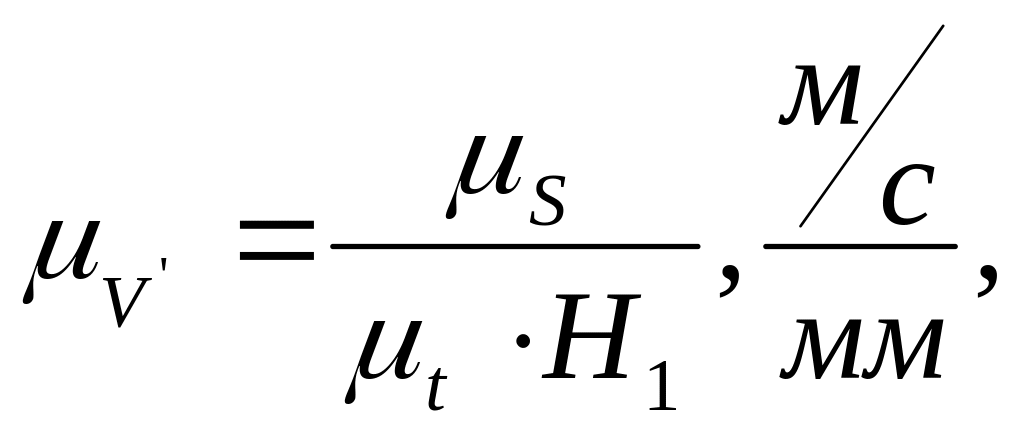
где _S – масштаб оси ординат диаграммы перемещения точки С;

_t – масштаб времени;

Н₁ – полюсное расстояние.

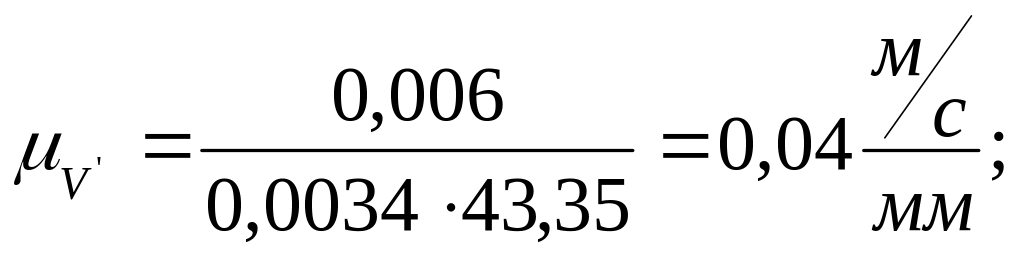
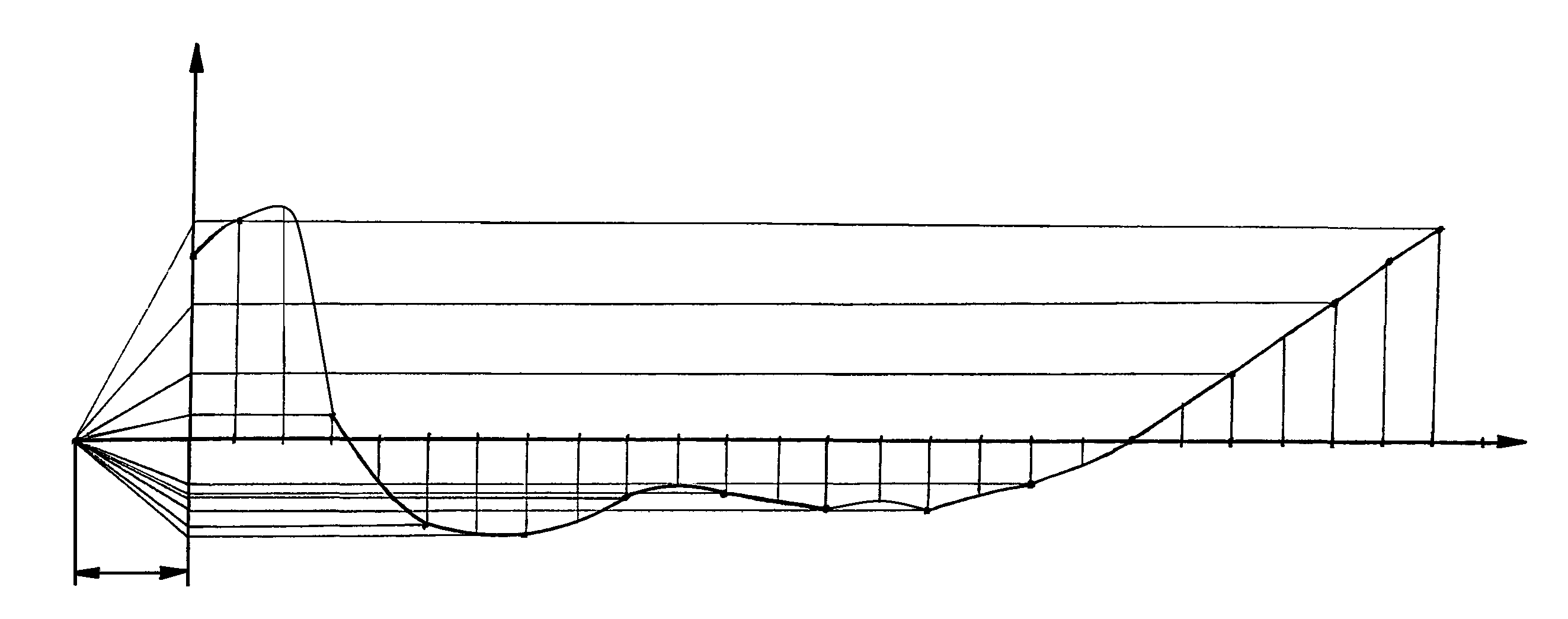
1.6 Построение диаграммы зависимости ускорения точки С от угла поворота ведущего звена W=W().

Построение осуществляем графическим дифференцированием диаграммы скорости точки С (рис.1.4,в). Для построения диаграммы на оси абсцисс откладываем отрезок l_0-12 =240 мм и разбиваем его на 12 равных частей, равных по величине отрезкам диаграммы скорости точки С. Вправо от отрезка l_0-12 на этой же оси откладываем длину еще одного отрезка, равного по величине тем, на которые разбит отрезок l_0-12. (получили тринадцать равных по величине отрезков). Влево от оси ординат откладываем полюсное расстояние Н₂. Выбирается произвольно (примем Н₂=39,2 мм). Получаем точку Р₂. На диаграмме скорости точки С соединяем прямыми линиями точки пересечения этой диаграммы с линиями, проведенными вдоль оси оу из точек 1, 2, 3 и т. д., находящихся на оси абсцисс данной диаграммы. Далее осуществляем действия, аналогичные тем, которые изложены выше в п. 1.5 при построении диаграммы скорости точки С. В данном случае точки пересечения середин отрезков 0-12 с линиями, параллельными оси абсцисс, называем 1’’’, 2’’’, 3’’’ и т. д. В середину отрезка 12-1 параллельным переносом сносим точку 1’’’, а также точку пересечения диаграммы ускорения и линии, проведенной вдоль оси оу из точки 1, расположенной на оси абсцисс. Соединяем эти две точки с точкой 12’’’. Из т.12 на оси абсцисс проводим линию вдоль оси ох до ее пересечения с графиком ускорения. Получаем некоторую точку. Т. к. т.12 соответствует точке 0, параллельным переносом перемещаем полученную точку на ось ординат. Соединяем полученную точку с точкой 1’’’ . Линии параллельного переноса и линии находящиеся «правее» точки 12 на оси абсцисс данной диаграммы, должны быть проведены пунктиром.

Масштаб оси ординат диаграммы перемещения определяется по следующей формуле:

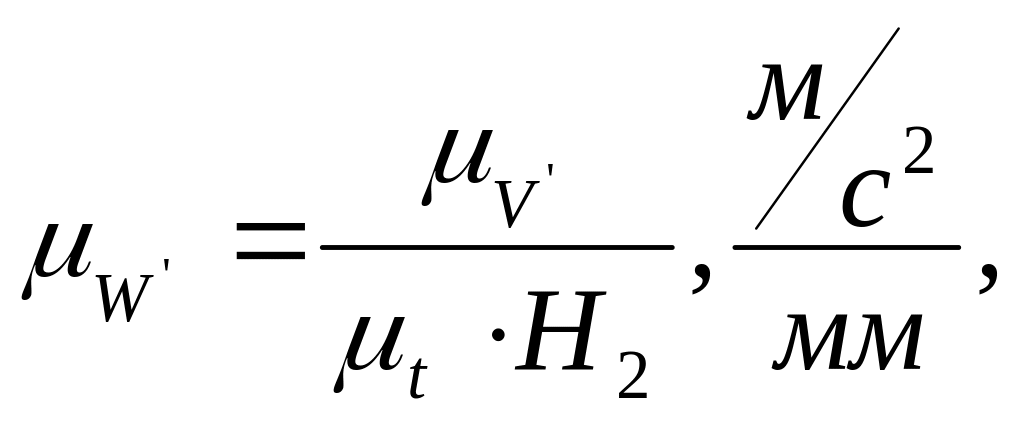
где - масштаб оси ординат диаграммы скорости точки С;

_t – масштаб времени;

Н₂ - полюсное расстояние.