
- •Неделько е.Ю. Лабараторный практикум по математической статистике
- •Лабораторная работа № 1 «Описание и группировка данных»
- •Пример выполнения лабораторной работы № 1 (вар. 0)
- •Пример выполнения лабораторной работы №2 (Вар. 0)
- •Задание №2. По второму столбцу выборки с составим непрерывный вариационный ряд и вычислим и .
- •"Элементы теории корреляции"
- •Пример выполнения лабораторной работы №3
- •Метод четырех полей
- •"Проверка гипотез"
- •Пример выполнения лабораторной работы №4
- •Пример выполнения лабораторной работы № 5
- •Приложение 1 Варианты заданий Вариант 0
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Критические точки распределения f Фишера – Снедекора
- •Уровень значимости
- •Уровень значимости
- •Приложение 6 Распределение Пуассона
- •Критические точки распределения .
Пример выполнения лабораторной работы № 5
Задание 1.
При уровне значимости проверить нулевую гипотезу о равенстве средних нескольких нормально распределенных генеральных совокупностей с неизвестными, но равными дисперсиями.
:
![]() ;
;
:
![]() .
.
Исходные данные помещены в таблицу 8
Таблица 8
|
Уровни фактора |
|||||
|
|
|
|
|
|
|
1 |
20 |
9 |
17 |
16 |
10 |
21 |
2 |
18 |
14 |
15 |
8 |
15 |
19 |
3 |
23 |
8 |
15 |
20 |
18 |
21 |
4 |
19 |
25 |
14 |
17 |
10 |
13 |
5 |
16 |
12 |
18 |
14 |
20 |
11 |
|
19,2 |
13,6 |
15,8 |
15 |
14,6 |
17 |
В таблице 8 – групповые средние подсчитаны по формуле
![]() ,
,
где
![]() – количество наблюдений на одном уровне.
– количество наблюдений на одном уровне.
Подсчитаем общую
среднюю
![]() по формуле
по формуле
![]() ,
,
где
![]() – количество уровней фактора F.
– количество уровней фактора F.
![]() .
.
Введем новые
переменные
![]() ,
где
,
где
![]() – условный нуль.
– условный нуль.
Вычислим общую, факторную и остаточную суммы квадратов отклонений по формулам:
 ,
(5)
,
(5)
 ,
(6)
,
(6)
![]() ,
(7)
,
(7)
где
![]() ;
;
![]() ;
;
 .
(8)
.
(8)
Новые переменные и некоторые вычисления приведены в таблице 9.
Таблица 9
j i |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
5 |
25 |
‑ 6 |
36 |
‑ 2 |
4 |
1 |
1 |
‑ 5 |
25 |
6 |
36 |
|
2 |
3 |
9 |
‑ 1 |
1 |
0 |
0 |
‑ 7 |
49 |
0 |
0 |
4 |
16 |
|
3 |
8 |
64 |
‑ 7 |
49 |
0 |
0 |
5 |
25 |
3 |
9 |
6 |
36 |
|
4 |
4 |
16 |
‑ 10 |
100 |
‑ 1 |
1 |
2 |
4 |
‑ 5 |
25 |
‑ 2 |
4 |
|
5 |
1 |
1 |
‑ 3 |
9 |
3 |
9 |
‑ 1 |
1 |
5 |
25 |
‑ 4 |
16 |
|
|
– |
115 |
– |
195 |
– |
14 |
– |
80 |
– |
84 |
– |
108 |
|
|
21 |
– |
‑ 7 |
– |
4 |
– |
0 |
– |
‑ 2 |
– |
10 |
– |
|
|
441 |
– |
49 |
– |
16 |
– |
0 |
– |
4 |
– |
100 |
– |
|
В результате вычислений по формулам (6), (7), (8), (9) получим:
![]() ;
;
![]() ;
;
![]() .
.
Вычислим факторную и остаточную дисперсии по формулам:
![]() ;
;
![]() .
.
Сравним факторную и остаточную дисперсию по критерию Фишера. Для этого найдем критическую точку правосторонней критической области, используя таблицу приложения 4.
![]() .
.
Вычислим наблюдаемое значение критерия
 .
.
Так как,
![]() ,
то факторная дисперсия и остаточная
различаются незначимо. Это означает,
что влияние фактора практически не
проявляется. Различие групповых средних
объясняется случайными причинами.
Нулевую гипотезу о равенстве средних
отвергать нет оснований. Для изучения
данного специального раздела математики
можно использовать любой из предлагаемых
источников.
,
то факторная дисперсия и остаточная
различаются незначимо. Это означает,
что влияние фактора практически не
проявляется. Различие групповых средних
объясняется случайными причинами.
Нулевую гипотезу о равенстве средних
отвергать нет оснований. Для изучения
данного специального раздела математики
можно использовать любой из предлагаемых
источников.
Задание 2.
На уровне значимости проверить нулевую гипотезу о равенстве средних нескольких нормально распределенных генеральных совокупностей с неизвестными, но равными дисперсиями. Количество наблюдений на различных уровнях фактора F различно:
: ;
: .
Исходные данные помещены в таблице 10
Таблица 10
j i |
Уровни фактора |
|
|||||
|
|
|
|
|
|
||
1 |
19 |
27 |
29 |
43 |
17 |
8 |
|
2 |
35 |
38 |
37 |
39 |
31 |
– |
|
3 |
25 |
36 |
29 |
22 |
12 |
– |
|
4 |
43 |
44 |
25 |
36 |
24 |
– |
|
5 |
– |
11 |
22 |
23 |
– |
– |
|
6 |
– |
33 |
– |
– |
– |
– |
|
7 |
– |
19 |
– |
– |
– |
– |
|
|
4 |
7 |
5 |
5 |
4 |
1 |
26 |
|
30,5 |
29,5 |
28,4 |
32,6 |
21 |
8 |
– |
В таблице 10 групповые
средние
вычислялись по формуле
![]() ,
где
,
где
![]() – количество наблюдений на j
– том уровне фактора.
– количество наблюдений на j
– том уровне фактора.
Общую среднюю
подсчитаем по формуле
![]() ,
где
,
где
![]() ,
– количество уровней фактора.
,
– количество уровней фактора.
![]() .
.
Вводим новые
переменные
![]() ,
где
,
где
![]() .
.
Вычисляем общую, факторную и остаточную сумму квадратов отклонений по формулам
 ,
(9)
,
(9)
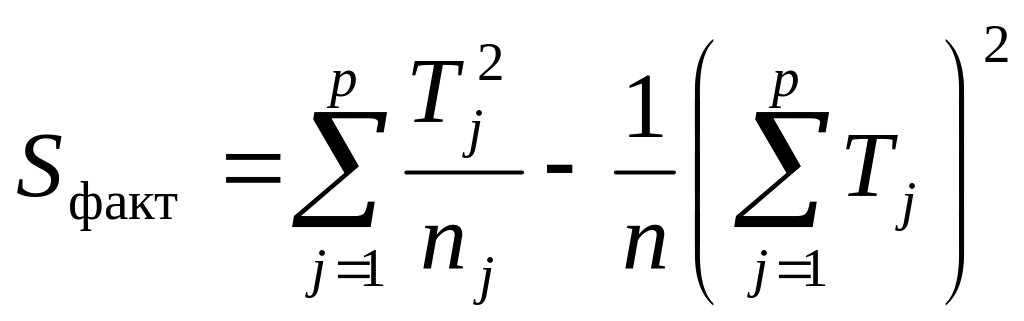 ,
(10)
,
(10)
![]() , (11)
, (11)
где
![]() ;
;
![]() .
(12)
.
(12)
Новые переменные и некоторые вычисления приведены в таблице 11.
Таблица 11
j i |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
-8 |
64 |
0 |
0 |
2 |
4 |
16 |
256 |
-10 |
100 |
-19 |
361 |
|
2 |
8 |
64 |
11 |
121 |
10 |
100 |
12 |
144 |
4 |
16 |
– |
– |
|
3 |
-2 |
4 |
9 |
81 |
2 |
4 |
-5 |
25 |
-15 |
225 |
– |
– |
|
4 |
16 |
256 |
17 |
289 |
-2 |
4 |
9 |
81 |
-3 |
9 |
– |
– |
|
5 |
– |
– |
-16 |
256 |
-5 |
25 |
-4 |
16 |
– |
– |
– |
– |
|
6 |
– |
– |
6 |
36 |
– |
– |
– |
– |
– |
– |
– |
– |
|
7 |
– |
– |
8 |
64 |
– |
– |
– |
– |
– |
– |
– |
– |
|
|
4 |
7 |
5 |
5 |
4 |
1 |
|
||||||
|
– |
388 |
– |
847 |
– |
137 |
– |
522 |
– |
350 |
– |
361 |
|
|
14 |
– |
19 |
– |
7 |
– |
28 |
– |
-24 |
– |
-19 |
– |
|
|
49 |
– |
51,6 |
– |
9,8 |
– |
156,8 |
– |
144 |
– |
361 |
– |
|
По формулам (9), (10), (11) с использованием таблицы 11 получим:
![]() ;
;
![]() ;
;
![]() .
.
Факторную и остаточную дисперсии найдем по формулам:
![]() ;
;
![]() .
.
Сравним факторную и остаточную дисперсии по критерию Фишера. Для этого вычислим
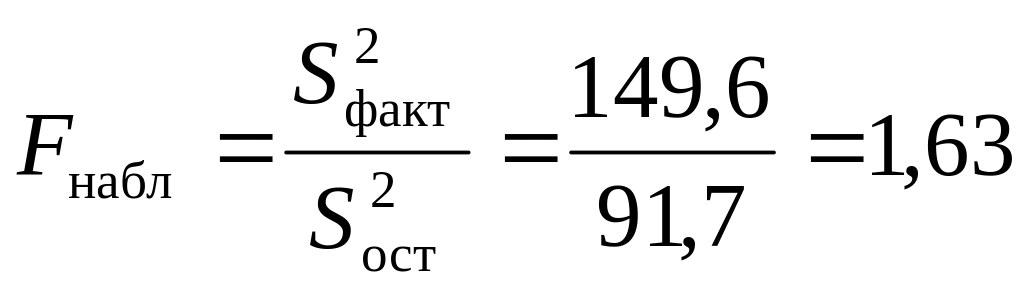 .
.
Критическую точку правосторонней критической области найдем по заданному уровню значимости ; используя таблицу приложения 4.
![]()
Поскольку
![]() ,
различие факторной и остаточной дисперсий
нельзя считать значимым. Следовательно,
нулевую гипотезу о равенстве средних
нельзя отвергать. Значит, уровень
подготовки спортсменов во всех
плавательных центрах в среднем одинаков.
Разница в результатах контрольных
соревнований объясняется случайными
причинами.
,
различие факторной и остаточной дисперсий
нельзя считать значимым. Следовательно,
нулевую гипотезу о равенстве средних
нельзя отвергать. Значит, уровень
подготовки спортсменов во всех
плавательных центрах в среднем одинаков.
Разница в результатах контрольных
соревнований объясняется случайными
причинами.
СПИСОК ЛИТЕРАТУРЫ
Гмурман В.Е. Теория вероятностей и математическая статистика. – М., 1997. – 368с.
Джонсон Н., Лион Ф. Статистика и планирование эксперимента в технике и науке. – М., 1980. – 610с.
Колде Я.К. Практикум по теории вероятностей и математической статистике. – М.: Изд. «Высшая школа», 1991. – 157с.
ПРИЛОЖЕНИЯ
