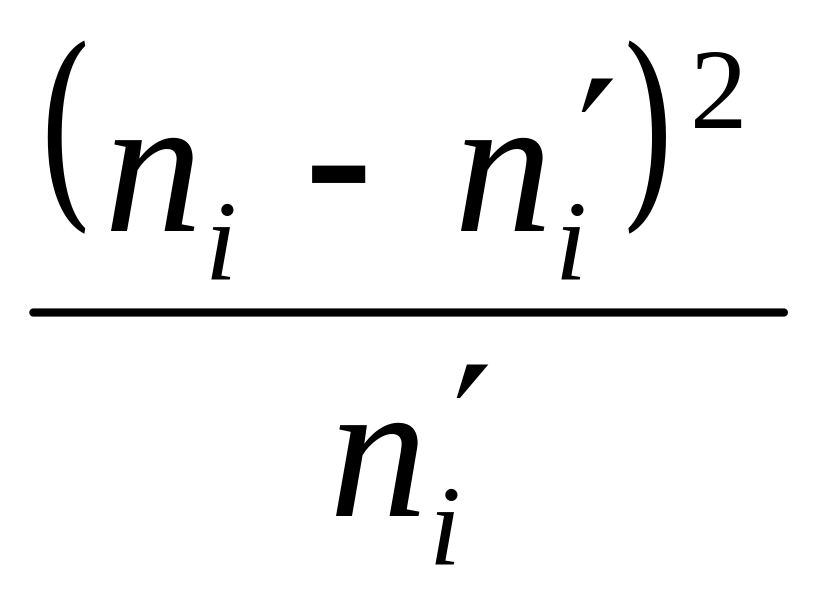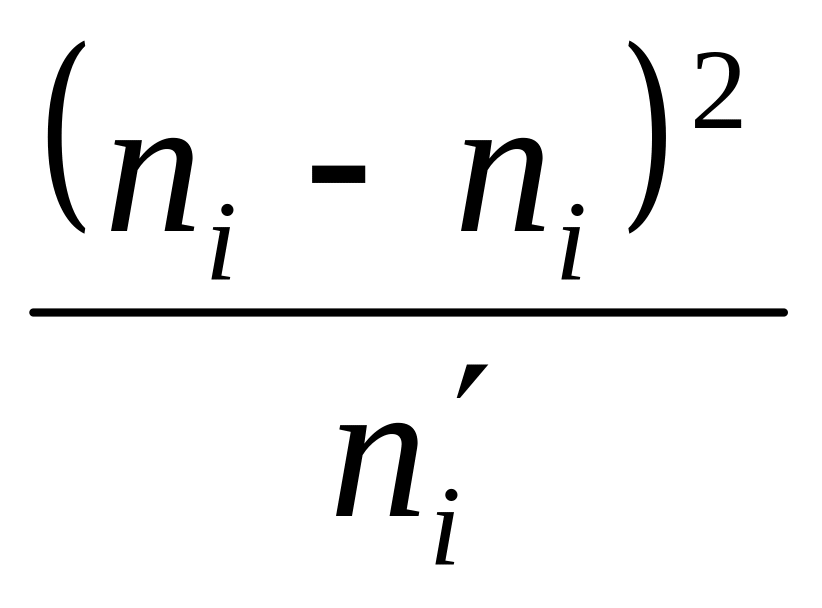"Проверка гипотез"
Задание 1.
По столбцам
и
выборки D
(приложение 1, вар 0) при уровне значимости
α проверить гипотезу о равенстве
дисперсий
:
;
:
,
используя критерий Фишера.
Принять
Задание 2.
По столбцам
и
выборки D
при уровне значимости α проверить
гипотезу о равенстве средних значений
:
;
:
,
если неизвестные дисперсии генеральных
совокупностей считать равными, используя
критерий Стюдента.
Принять
.
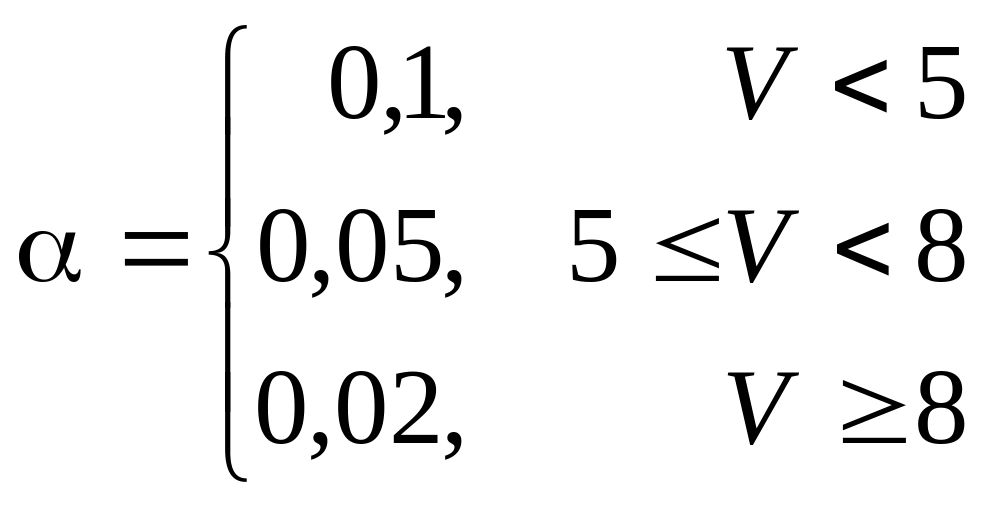
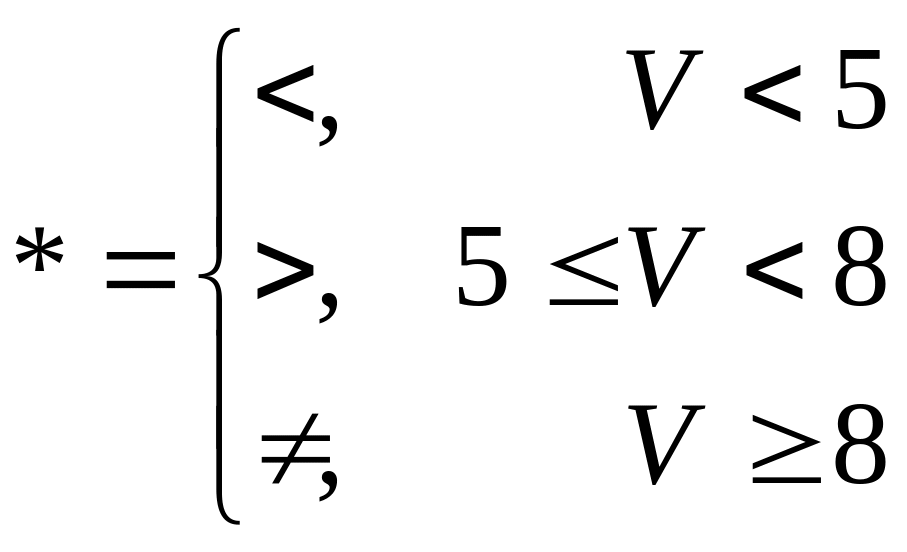Здесь V
– номер варианта.
Задание 3. Используя результаты лабораторной работы № 2, провести проверку гипотезы о значимости выборочного коэффициента корреляции.
Принять
Задание 4. По выборке A при уровне значимости проверить гипотезу о распределении Пуассоа соответствующей генеральной совокупности.
Принять
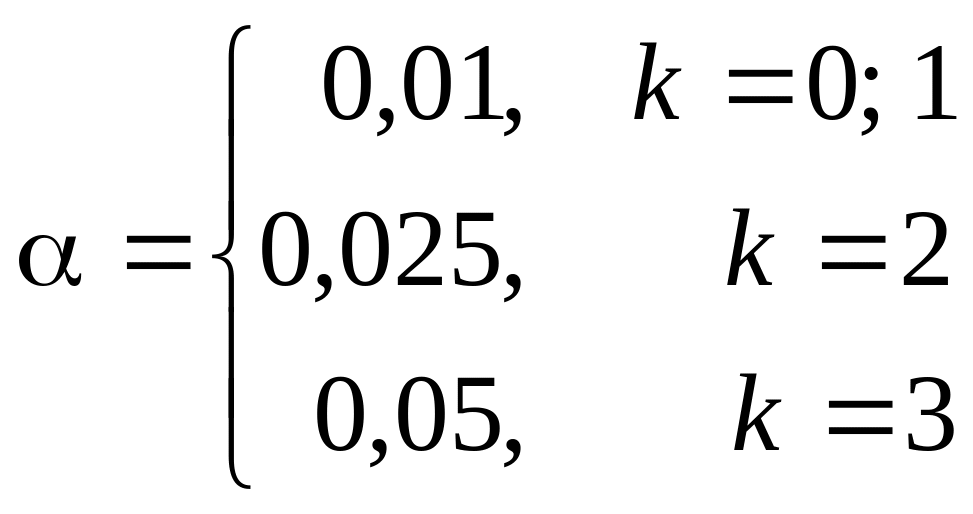где k
– остаток
.
Задание 5. По выборке B при уровне значимости проверить гипотезу о нормальном распределении соответствующей генеральной совокупности.
Принять
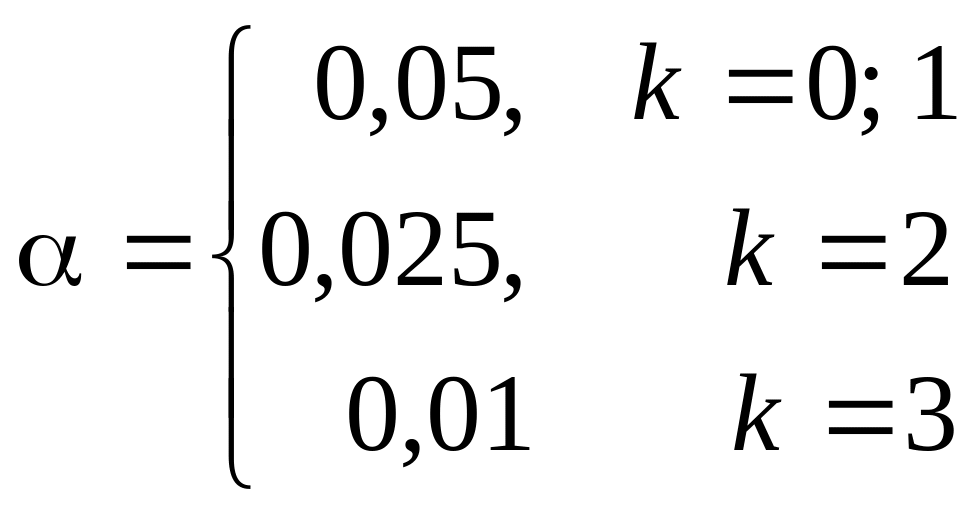где k
– остаток
.
Пример выполнения лабораторной работы №4
Задание 1.
При уровне значимости
необходимо проверить нулевую гипотезу
(
)
о равенстве дисперсий двух генеральных
совокупностей
при альтернативной гипотезе
:
.
Исходные данные:
|
17 |
15 |
15 |
14 |
18 |
|
16 |
8 |
20 |
17 |
14 |
Вычисляем наблюдаемое значение критерия
,
где
– большая исправленная дисперсия,
‑ меньшая исправленная дисперсия.
Исправленную дисперсию определяем по формуле:
,
где n
– объем выборки,
– дисперсия выборки.
Найдем выборочные средние
;
;
;
.
;
;
;
;
.
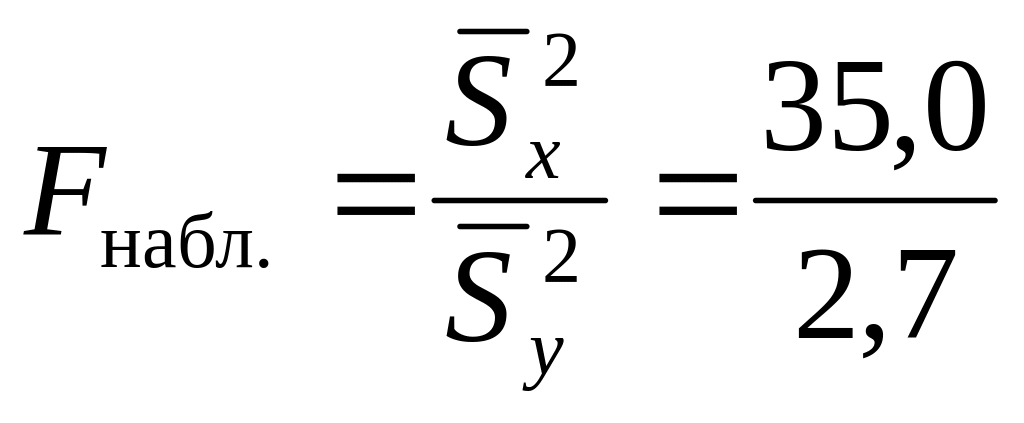Основываясь на форме альтернативной гипотезы , строим правостороннюю критическую область.
Критическую точку правосторонней критической области находим по таблице критических точек распределения Фишера (см. приложение 4)
,
где α – заданный
уровень значимости,
;
– числа степеней свободы большей и
меньшей дисперсии соответственно.
Так
как
,
нет оснований отвергнуть нулевую
гипотезу. Есть основание полагать
генеральные дисперсии равными. Различие
же выборочных дисперсий может быть
объяснено случайными причинами, например,
малым объемом выборки.
Задание 2.
При уровне значимости
необходимо проверить гипотезу о равенстве
средних двух генеральных совокупностей
:
при альтернативной гипотезе
:
.
Считаем дисперсии генеральных совокупностей неизвестными, но равными
Исходные данные
|
20 |
18 |
23 |
19 |
16 |
|
9 |
14 |
8 |
25 |
12 |
Наблюдаемое значение критерия находим по формуле:
,
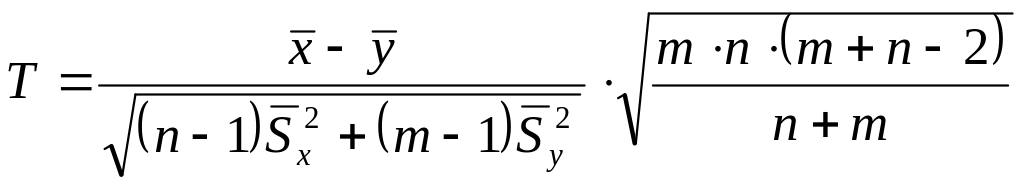где
,
‑ выборочные средние;
,
– выборочные исправленные дисперсии;
n,
m
– объемы выборок.
;
;
;
.
;
;
;
.
Вычисляем
.
В соответствии с
видом конкурирующей гипотезы
:
,
– строим левостороннюю критическую
область.
Для поиска критической точки воспользуемся таблицей критических точек распределения Стьюдента (см. приложение 4).
.
Так как
,
то нет оснований отвергать нулевую
гипотезу о равенстве генеральных средних
.
Задание 3.
В лабораторной
работе №2 по выборке объема
найден выборочный коэффициент корреляции
(
)
переменных величин x
и y.
Требуется при уровне значимости
проверить нулевую гипотезу о равенстве
нулю генерального коэффициента корреляции
:
при альтернативной гипотезе
:
.
Наблюдаемое значение критерия находится по формуле
.
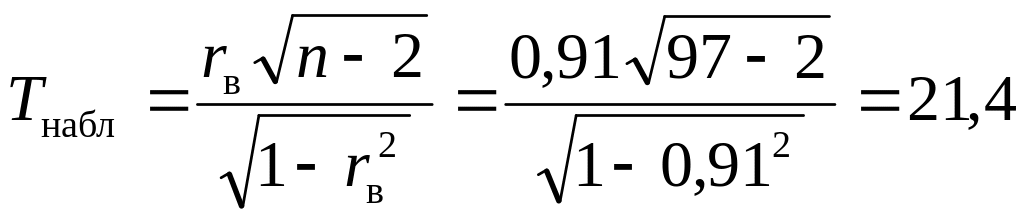В соответствии с видом альтернативной гипотезы : строим двустороннюю критическую область.
Критическую точку находим с помощью таблиц критических точек распределения Стьюдента (см. приложение 5).
.
Так как
(
),
то есть наблюдаемое значение критерия
попало в критическую область, нулевую
гипотезу следует отвергнуть и принять
альтернативную
.
Значит x
и y
коррелированны и связаны линейной
зависимостью.
Задание 4.
При уровне значимости проверить нулевую гипотезу ( ) о распределении генеральной совокупности по закону Пуассона. Альтернативная гипотеза ( ): распределение генеральной совокупности не соответствует распределению Пуассона.
В качестве критерия проверки нулевой гипотезы принимается случайная величина
,
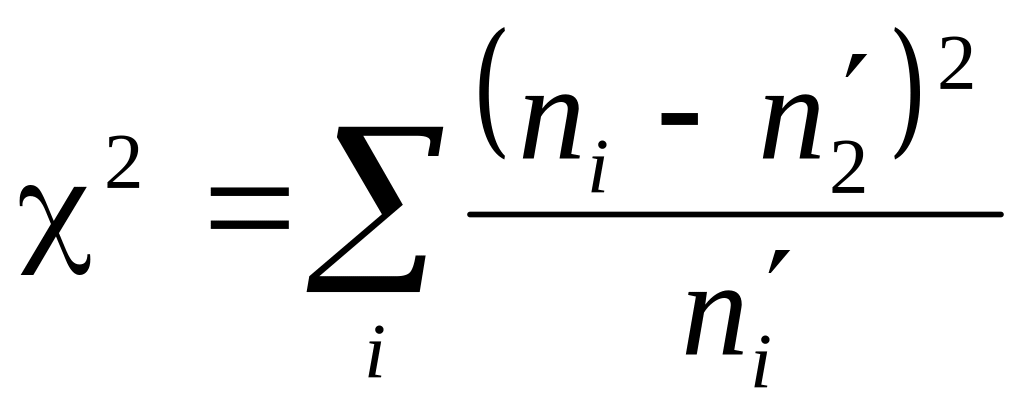(5)
где
‑ эмпирическая частота,
‑ теоретическая частота, вычисление
в предположении, что изучаемая генеральная
совокупность распределена (в данном
случае) по закону Пуассона.
При выполнении
лабораторной работы №1 по выборке A
построен дискретный вариационный ряд
(табл. 1) и найдены среднее значение
и дисперсия
.
Параметром распределения Пуассона
является .
Известно, что для этого распределения
.
Оценки математического ожидания (
)
и дисперсии (
)
близки по значению, но не равны. В таблице
распределения Пуассона (таблица
приложения 6) найдем ближайшее к ним
.
Проверим гипотезу при
.
Частоты трех последних значений малы
(табл. 1), поэтому объединяем их в один
интервал.
Для вычисления
наблюдаемого значения
построим табл. 8.
Табл. 8
i |
|
|
|
|
|
|
|
1 2 3 4 5 6 |
0 1 2 3 4 5 |
7 11 14 18 11 3 |
0,1353 0,2707 0,2707 0,1804 0,0902 0,0529 |
8,7 17,3 17,3 11,8 5,8 3,4 |
‑ 1,7 ‑ 6,3 ‑ 3,3 6,2 5,2 ‑ 0,4 |
2,98 39,63 10,89 38,44 27,04 0,16 |
0,332 2,294 0,630 3,258 4,662 0,047 |
|
|
|
1,0056 |
64,3 |
|
|
|
Замечание 1.
В таблице 8 столбец
(вероятностей распределения Пуассона)
взят из таблицы приложения 6 для значения
,
причем вероятность значения
получено суммированием вероятностей
после значения
.
В результате .
Для проверки
гипотезы выбираем правостороннюю
критическую область. Критическую точку
найдем по таблице приложения 7, где
уровень значимости,
‑ число степеней свободы, s
– количество интервалов, r
– число параметров предполагаемого
распределения. В описанном случае
,
.
В итоге
.
Таким образом
.
Критическая область с нанесенной на нее имеет вид
Вывод.
Так как
,
нет оснований отвергать нулевую гипотезу
о распределении генеральной совокупности
по закону Пуассона.
Задание 5.
По выборке B при уровне значимости проверить нулевую гипотезу ( ) о распределении генеральной совокупности по нормальному закону. Альтернативная гипотеза ( ): распределение генеральной совокупности не отвечает нормальному распределению.
В качестве критерия
проверки нулевой гипотезы принимается
случайная величина
(формула 5).
При выполнении лабораторной работы №1 по выборке B получен непрерывный вариационный ряд (табл. 3). Используем его и приступим к определению наблюдаемого значения критерия .
Разобъем этот процесс на два этапа. Первый – определение теоретических частот нормального распределения . Второй ‑ собственно подсчет . Для определения частот составим табл. 9.
Табл. 9
|
|
|
|
|
|
|
|
|
|
|
1 2 3 4 5 6 7 8 9 10 |
48 51 54 57 60 63 66 69 72 75 |
51 54 53 60 63 66 69 72 75 76 |
‑ ‑ 11,5 ‑ 8,5 ‑ 5,5 ‑ 2,5 0,5 3,5 6,5 9,5 12,5 |
‑ 11,5 ‑ 8,5 ‑ 5,5 ‑ 2,5 0,5 3,5 6,5 9,5 12,5 15,5 |
‑ ‑ 2,1 ‑ 1,55 ‑ 1,0 ‑ 0,46 0,09 0,64 1,19 1,73 2,28 |
‑2,1 ‑1,55 ‑1,0 ‑0,46 0,09 0,64 1,19 1,73 2,28 |
‑ 0,5 ‑ 0,4821 ‑ 0,4394 ‑ 0,3413 ‑ 0,1772 0,0359 0,2389 0,3830 0,4582 0,4887 |
‑ 0,4821 ‑ 0,4394 ‑ 0,3413 ‑ 0,1772 0,0359 0,2389 0,3830 0,4582 0,4887 0,5 |
0,0179 0,0427 0,0981 0,1641 0,2131 0,203 0,1441 0,0752 0,0305 0,0113 |
2,88 6,87 15,79 26,42 34,31 32,68 23,20 12,11 4,91 1,82 |
|
|
|
|
|
|
|
|
|
1 |
161 |
В табл. 9 обозначено
;
;
;
;
,
‑ значения функции Лапласа из таблицы
приложения 8;
;
.
Для подсчета составим табл. 10.
Табл. 10
|
|
|
|
|
|
|
|
1 |
2 |
2,88 |
‑ 0,88 |
0,77 |
0,27 |
4 |
1,39 |
2 |
7 |
6,87 |
0,23 |
0,05 |
0,007 |
49 |
7,13 |
3 |
21 |
15,79 |
5,21 |
27,14 |
1,71 |
441 |
27,93 |
4 |
22 |
26,42 |
‑ 4,42 |
19,54 |
0,74 |
484 |
18,32 |
5 |
31 |
34,31 |
‑ 3,31 |
10,96 |
0,32 |
961 |
28,01 |
6 |
34 |
32,68 |
1,32 |
1,74 |
0,05 |
1156 |
35,37 |
7 |
27 |
23,20 |
3,8 |
14,41 |
0,62 |
729 |
31,42 |
8 |
11 |
12,11 |
‑ 1,11 |
1,23 |
0,10 |
121 |
9,99 |
9 |
4 |
4,91 |
‑ 0,91 |
0,83 |
1,17 |
16 |
3,26 |
10 |
2 |
1,82 |
0,08 |
0,006 |
0,004 |
4 |
2,20 |
|
161 |
161 |
|
|
|
|
165,02 |
В таблице 10 последние два столбца приведены для контроля вычислений. Если они выполнены тщательно, то должно быть
.
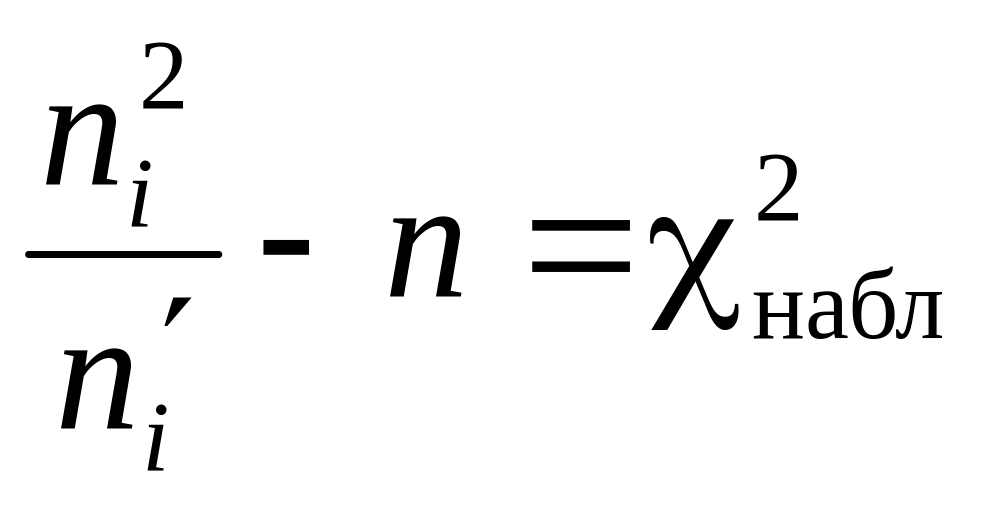В нашем случае
,
что практически совпадает с найденным .
Критическую точку
правосторонней кртической области
найдем по таблице приложения 7.
.
Нанесем наблюдаемое значение на критическую область
Вывод.
Поскольку наблюдаемое значение не попало в критическую область ( ), нет оснований отвергать нулевую гипотезу о распределении генеральной совокупности по нормальному закону.
ЛАБОРАТОРНАЯ РАБОТА № 5
“Однофакторный дисперсионный анализ”
В работе задействованы два массива данных.
Выборка D.
Результаты тестирования студентов,
изучающих специальный раздел математики
по разным методикам, например,
– конспект лекций,
– справочное пособие и т.д. Тестирование
проводится на предмет изучения вопроса
о равноценности источников.
Задание 1. На уровне значимости α требуется проверить гипотезу о равенстве средних значений для всех уровней фактора F.
Выборка Е.
Результаты контрольных соревнований
спортсменов, прошедших подготовку в
различных (
)
плавательных центрах. Цель соревнований
– определить одинаков ли в среднем
уровень подготовки во всех центрах.
Задание 2. На уровне значимости α требуется проверить гипотезу о равенстве средних значений для всех уровней фактора F.
Уровень значимости принять: 0,01 – четный вариант; 0,05 – нечетный вариант.