Метод четырех полей

U V	-2		-1		0	1		2		3		I	II
-2		4	‑			‑		‑		‑		4	‑
	1
-1		2		1		‑		‑		‑		9	‑
	2		5
0												III	IV
1	‑		‑				1					‑	16
						16
2	‑		‑				2		4			‑	46
						9		7
3	‑		‑						6		9	‑	57
								8		1
4	‑		‑								12	‑	48
										4
I	8		5		II	34		‑		‑		13	‑
III	‑		‑		IV	34		76		57		‑	167

Значение используемого слагаемого найдем суммированием чисел в четырех клетках таблицы 3.

.

Найдем коэффициент корреляции

.

Величины , , , найдем по формулам

;

;

;

.

В результате уравнения регрессии будут выглядеть так.

;

. (3)

;

. (4)

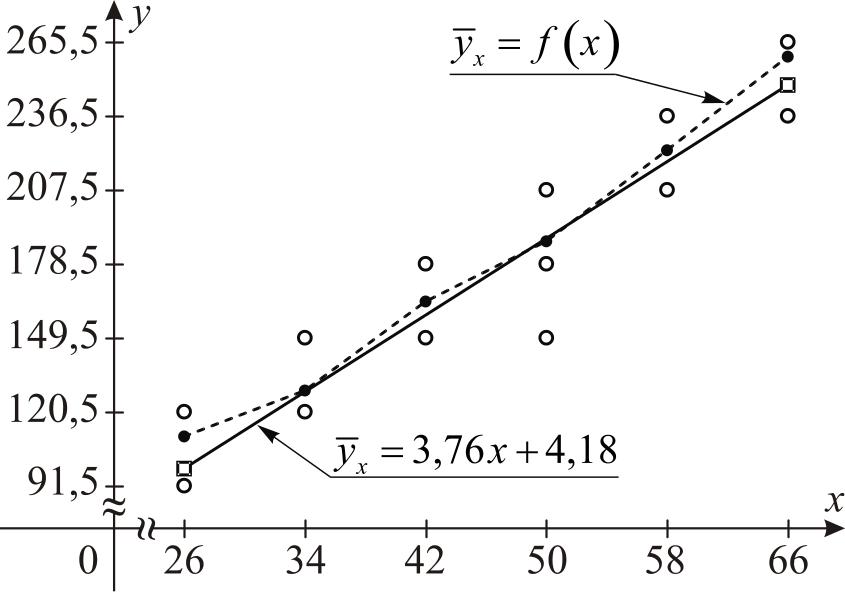
Построим графики эмпирической регрессии (по данным табл. 5) и прямые регрессии (форм. (3), (4)). На этих же графиках построим корреляционное поле XY.

Рис. 5. Корреляционное поле (○ ○ ○), линии эмпирической (● ● ●) и теоретической регрессии (□ □)

Рис. 6. Корреляционное поле (○ ○ ○), линии эмпирической (● ● ●) и теоретической регрессии (□ □)

Задание 4

Стандартную ошибку оценки определяем по формуле:

.

Оценка коэффициента корреляции генеральной совокупности производится по соотношению:

;

;

;

.

Вывод

1. Между переменными x и y соответствует глубокая положительная ( 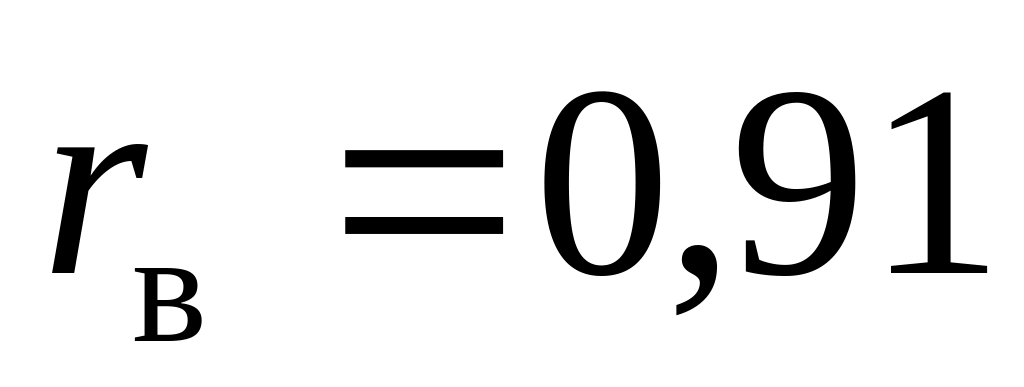) корреляционная связь.

2. С вероятностью 0,9973 коэффициент корреляции генеральной совокупности покрывается интервалом .

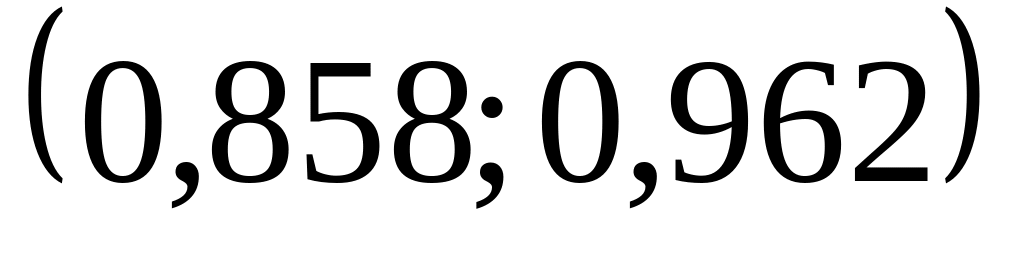ЛАБОРАТОРНАЯ РАБОТА № 4