Министерство образования и науки, молодежи и спорта Украины

Национальный университет кораблестроения

имени адмирала Макарова

Неделько е.Ю. Лабараторный практикум по математической статистике

Николаев 2013

УДК

ББК

ВВЕДЕНИЕ

Настоящее методическое пособие предназначено для студентов технических специальностей, изучающих курс математической статистики. Теоретические знания предлагается закрепить в форме выполнения лабораторных работ, охватывающих следующие разделы: первичная обработка данных эксперимента, теория оценивания, корреляционный анализ, теория статистического вывода, дисперсионный анализ.

Каждая из предлагаемых лабораторных работ соровождается примером выполнения. Все вычисления проведены в форме «ручного счета», что, с точки зрения автора, весьма полезно для углубленного понимания курса. Вместе с тем вполне возможно применение современных компъютерных программ для практической реализации поставленных в изучаемом курсе задач.

Практическая ценность данного пособия состоит в том, что студент получает необходимые навыки комплексного статистического анализа результатов экспериментальных исследований.

Исходные данные для выполнения лабораторных работ представлены в виде выборок.

Выборка А. Количество дефектов, обнаруженных в N сварных швах одинаковой длины в результате ручной електросварки.

Выборка B. Абсолютное удлинение (мм.) при растяжении N образцов полимерного материала.

Выборка C. Результаты эксперимента по изучению взаимосвязи времени выдержки (в часах) образцов полимерного материала под нагрузкой (переменная X) и абсолютным удлинением (в мм.) при разрушении (переменная Y).

Выборка D. Результат тестирования (в баллах) студентов, изучающих специальный раздел высшей математики по различным источникам, например: F₁ – конспект лекций, F₂ – справочник и т.д.. Тестирование проводится на предмет изучения вопроса о равноценности источников.

Выборка E. Результаты контрольных соревнований (в баллах), прошедших подготовку в разных плавательных центрах. Цель соревнований – определить одинаков ли в среднем уровень подготовки во всех плавательных центрах.

Лабораторная работа № 1 «Описание и группировка данных»

Задание 1. По выборкам А и В составить дискретный и непрерывный вариационные ряды. По выборке А построить полигон и гистограмму частот, по выборке В – полигон и гистограмму относительных частот.

Задание 2. Найти основные числовые характеристики вариационных рядов: среднее значение ( ); моду (M₀) медиану (M_e); размах варьирования (R); дисперсию (S²), стандартное отклонение (S), коэффициент вариации (V_x), асимметрию (А_s), эксцесс (Е). По выборке А вычислить (нечётные варианты), (чётные варианты). По выборке В вычислить , (нечётные варианты), , (чётные варианты).

Пример выполнения лабораторной работы № 1 (вар. 0)

По выборке А (приложение 1, вар 0) строим дискретный вариационный ряд (Табл. 1), который дополняем столбцами, используемыми для определения числовых характеристик.

Табл. 1

i
1	0	7	0	0	0
2	1	11	11	1	11
3	2	14	28	4	56
4	3	18	54	9	162
5	4	11	44	16	176
6	5	1	5	25	25
7	6	1	6	36	36
8	7	1	7	49	49
		64	155		515

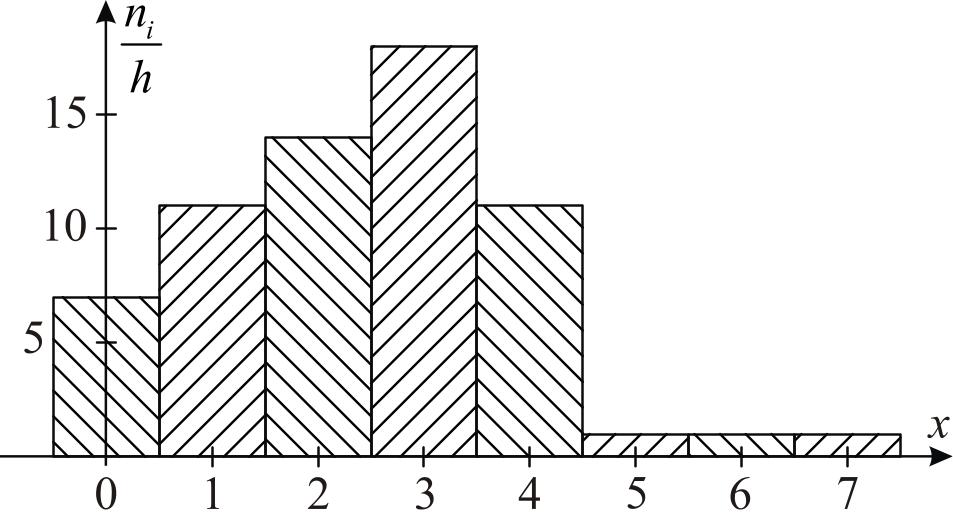
Строим полигон (рис.1) и гистограмму частот (рис.2).

Рис. 1. Полигон частот

Рис. 2. Гистограмма частот ( )

Вычисляем основные характеристики (см. табл. 1).

1) – среднее значение. .

2) – мода; .

3) – медиана; .

4) – дисперсия; ; .

5) ‑ стандартное отклонение; ; .

6) – коэффициент вариации; .

Для определения асимметрии и эксцесса построим табл.2:

Табл. 2

i
1	0	-2,42	-14,2	-99,4	34,3	240,1	7
2	1	-1,42	-2,86	-31,5	4,07	44,7	11
3	2	-0,42	-0,07	-0,98	0,031	0,43	14
4	3	0,58	0,195	3,51	0,11	2,04	18
5	4	1,58	3,94	43,3	6,23	68,6	11
6	5	2,58	17,2	17,2	44,3	44,3	1
7	6	3,58	45,9	45,9	164,3	164,3	1
8	7	4,58	96,1	96,1	440,0	440,0	1
				74,13		1004,5	64

7) – асимметрия; ; .

8) Е ‑ эксцесс; ; .

По выборке В (приложение 1, вар 0) строим непрерывный вариационный ряд (табл.3).

Табл. 3 ( ; )

i
1 2 3 4 5 6 7 8 9 10	48-51 51-54 54-57 57-60 60-63 63-66 66-69 69-72 72-75 75-78	2 7 21 22 31 34 27 11 4 2	2 9 30 52 83 117 144 155 159 161	49,5 52,5 55,5 58,5 61,5 64,5 67,5 70,5 73,5 76,5	-15 -12 - 9 - 6 - 3 0 3 6 9 12	-10 -28 -63 -44 -31 0 27 22 12 8	50 112 189 88 31 0 27 44 36 32	0,004 0,014 0,043 0,046 0,064 0,07 0,06 0,02 0,008 0,004
		161				-107	609

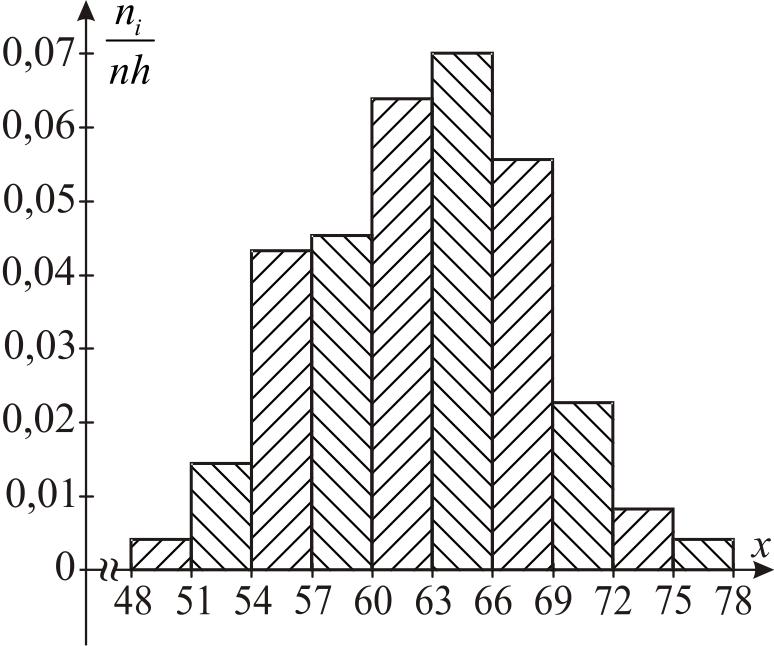
Строим полигон (рис.3) и гистограмму относительных частот (рис.4).

Рис. 3. Полигон относительных частот

Рис. 4. Гистограмма относительных частот

Вычисляем основные характеристики (см. табл. 3).

1) – среднее значение; .

2) – мода; .

3) – медиана; .

4) – дисперсия; ; .

5) – стандартное отклонение; ; .

6) – коэффициент вариации; ; .

Для определения асимметрии и эксцесса строим табл. 4.

Табл. 4 ( )

i
1 2 3 4 5 6 7 8 9 10	49,5 52,5 55,5 58,5 61,5 64,5 67,5 70,5 73,5 76,5	2 7 21 22 31 34 27 11 4 2	-13 -10 -7 -4 -1 2 5 8 11 14	-2197,0 -1000,0 -343,0 -64 -1 8 125 512 1331 2744	-4394,0 -7000,0 -7203,0 -1408,0 -31,0 272 3375 5632 5324 5488	28561 10000 2401 256 1 16 625 4096 14641 38416	57122 70000 50421 5632 31 544 16875 45056 58564 76832
					55		381077

7) – асимметрия; ; .

8) – эксцесс; ; .

ЛАБОРАТОРНАЯ РАБОТА № 2

“Теория оценивания”

Задание №1. По 3 и 4 столбцу ( и ) выборки D вычислить несмещенные оценки математического ожидания а, дисперсии и среднего квадратического отклонения  генеральной совокупности, распределенной нормально.

Задание №2. По второму столбцу Y выборки С вычислить несмещенные оценки параметров генеральной совокупности а, , . (Предварительно составить непрерывный вариационный ряд).

Задание №3. Используя выборки из заданий 1 и 2, найти доверительный интервал для оценки математического ожидания а (при неизвестном ) и среднего квадратического отклонения  при доверительной вероятности .

Доверительную вероятность  принять:

где V – номер варианта.

Задание №4. Считая выборки из задания 1 пробными, найти минимальный объем выборки для определения доверительного интервала математического ожидания а с точностью  и доверительной вероятностью .

Доверительную вероятность  и точность  принять: