
Вивчення законів коливання фізичного маятника
Мета роботи.
Вивчити закономірності затухаючих механічних коливань фізичного маятника, визначити характеристики таких коливань.
Прилади і обладнання
1. Фізичний маятник.
2. Електронний секундомір.
Самостійна підготовка.
1. Студент вивчає правила роботи з установкою.
2. Вивчає теорію коливань фізичного і математичного маятників.
3. Вивчає теорію і методику проведення експерименту.
Теоретичні відомості
 Фізичним
маятником зветься тверде тіло, яке має
можливість коливатися під дією власної
ваги
Фізичним
маятником зветься тверде тіло, яке має
можливість коливатися під дією власної
ваги
![]() біля нерухомої горизонтальної осі О,
що не проходить через його центр інерції
біля нерухомої горизонтальної осі О,
що не проходить через його центр інерції
![]() (рис. 1).
(рис. 1).
У положенні рівноваги центр інерції
маятника
знаходиться під точкою підвісу О
на вертикальній лінії. Якщо відхилити
фізичний маятник від положення рівноваги
на кут
![]() ,
то виникне момент сили ваги маятника,
який повертає його до положення рівноваги.
,
то виникне момент сили ваги маятника,
який повертає його до положення рівноваги.
Основний закон обертального руху твердого тіла в механіці в узагальненій формі має вигляд
![]() ,
( 1)
,
( 1)
де
![]() –
час,
–
час,
![]() – вектор моменту імпульсу тіла,
– вектор моменту імпульсу тіла,
![]() –
вектор моменту сил, які діють на тіло.
–
вектор моменту сил, які діють на тіло.
У наближенні малих відхилень, при яких
![]() ,
при врахуванні тільки сили ваги,
диференціальне рівняння ( 1) дає рівняння
руху маятника у вигляді гармонічних
коливань:
,
при врахуванні тільки сили ваги,
диференціальне рівняння ( 1) дає рівняння
руху маятника у вигляді гармонічних
коливань:
![]() ,
( 2)
,
( 2)
де
![]() – амплітуда коливань,
– амплітуда коливань,
![]() – циклічна частота власних коливань
маятника,
– циклічна частота власних коливань
маятника,
![]() – початкова фаза,
– початкова фаза,
![]() . Період цих коливань є
. Період цих коливань є
![]() ( 3)
( 3)
де J – момент інерції маятника відносно осі О, g – прискорення вільного падіння, m – маса маятника, l – відстань ОС.
Якщо тіло маятника побудовано так, що його маса зосереджена біля точки С (матеріальна точка з масою m на невагомому підвісі довжиною l), то маятник називається математичним. В цьому випадку J=ml2, а період коливань має вигляд
![]() .
( 4)
.
( 4)
При врахуванні сил тертя маятника з
навколишнім середовищем, які діють
проти руху маятника і гальмують його,
розв’язок диференціального рівняння
( 1) (коли не дуже великі сили тертя й
![]() )
є
)
є
![]() ( 5)
( 5)
де
![]() ( 6)
( 6)
![]() ( 7)
( 7)
 Рівняння
руху маятника ( 5) є рівнянням гармонічних
коливань із частотою ω та амплітудою
A(t), яка зменшується згідно з
формулою (6). При цьому, як випливає з
формули (7), частота ω<ω0.
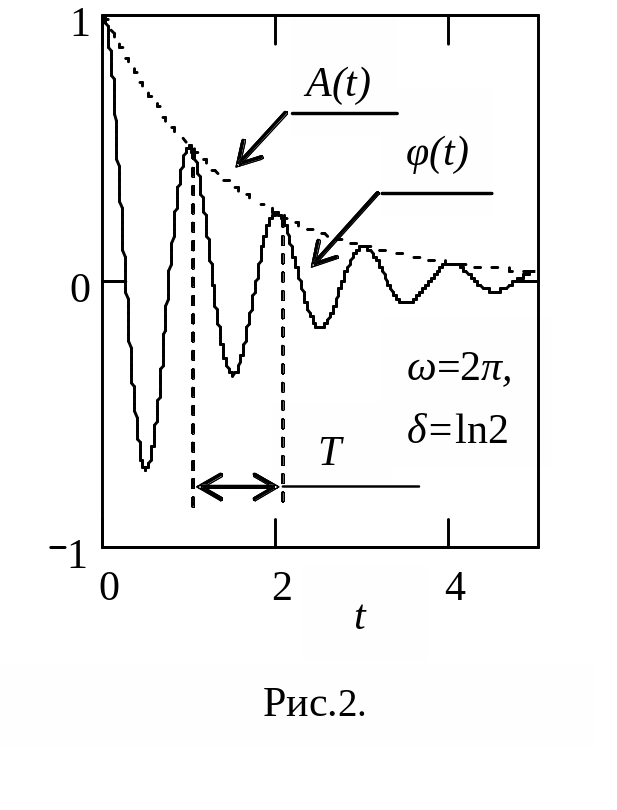
Приклад вигляду функцій φ(t),
A(t) при δ=ln2, ω=2π
наведений на рис. 2. Зменшення амплітуди
коливань обумовлено втратою енергії
маятником при виконанні ним роботи
проти сил тертя. Коефіцієнт загасання
δ=1/τ визначає швидкість зменшення
амплітуди, а проміжок часу τ, за який
амплітуда зменшується у e разів,
називається часом релаксації. Період
загасаючих коливань не дорівнює Т0,
він дається виразом:
Рівняння
руху маятника ( 5) є рівнянням гармонічних
коливань із частотою ω та амплітудою
A(t), яка зменшується згідно з
формулою (6). При цьому, як випливає з
формули (7), частота ω<ω0.
Приклад вигляду функцій φ(t),
A(t) при δ=ln2, ω=2π
наведений на рис. 2. Зменшення амплітуди
коливань обумовлено втратою енергії
маятником при виконанні ним роботи
проти сил тертя. Коефіцієнт загасання
δ=1/τ визначає швидкість зменшення
амплітуди, а проміжок часу τ, за який
амплітуда зменшується у e разів,
називається часом релаксації. Період
загасаючих коливань не дорівнює Т0,
він дається виразом:
![]() ( 8)
( 8)
Добуток коефіцієнта загасання на період коливань ε=δТ називається логарифмічним декрементом загасання. Він задовольняє виразу
![]() ( 9)
( 9)
Вираз (6) може бути представленим у вигляді
lnA(t)=lnA0 – δt. (10)
Рівняння (10) є рівнянням прямої лінії у координатах lnA – t, а коефіцієнт
![]() (11)
(11)
визначає нахил цієї прямої лінії до осі часу (рис .3). Ця формула може бути використана для експериментального визначення коефіцієнта загасання, якщо виміряна залежність амплітуди від часу. Тоді він дається виразом
![]() (12)
(12)
 Знання,
які потрібно мати при виконанні роботи
Знання,
які потрібно мати при виконанні роботи
Для виконання роботи потрібно:
вивчити наступні розділи: обертальний рух, механічні коливання, математичний маятник, фізичний маятник, вільні гармонічні коливання, загасаючі коливання;
вміти отримати вираз (5).
