3 Қос интеграл

3.1 Тік бұрышты координаттар жүйесіндегі қос интегралдар

жазықтығының жабық D облысында анықталған функциясы берілсін. D облысын кез келген жолмен n жай облыстарға бөлейік. Осы жай (қарапайым) облыстардың аудандарын деп, ал сәйкес диаметрлерін арқылы белгілейік, мұндағы облыс диаметрі деп осы облыста жатқан кез келген екі нүктесінің ара қашықтықтарының ең үлкенін айтады. Әрбір жай облыстан кез келген бір нүктеден таңдап алып, осы нүктелердегі анықталатын функциялардың мәндерін сәйкес аудандарына көбейтіп қолдансақ

Осы қосынды функцияның D облысындағы интегралдық қосындысы деп аталады.

Егер интегралдық қосындының шегі бар және ол шек D облысын n жай облыстарға қалай бөлгенімізге де, әрбір жай облыстан М₁ нүктелерін қалай алғанымызға да байланысты болмаса, одна осы шек функциясының D облысындағы қос интегралы деп аталады да былай белгіленеді:

Егер D облысында болса, онда екі еселі интегралы жоғарыдан бетімен, бүйір жағынан D облысының шекарасы арқылы өтетін Оz осіне параллель болатын цилиндр бетімен, төменнен Оху жазықтығымен шектелген цилиндрлік дененің көлеміне тең болады.

Е к і е с е л і и н т е г р а л д ы ң н е г і з г і қ а с и е т т е р і:

1.

2. мұндағы С – тұрақты сан.

3. Егер D облысын D₁ және D₂ облыстарына бөлсек, онда

4. Егер D облысында болса, онда

5. Е к і е с е л і и н т е г р а л д ы б а ғ а л а у. Егер болса, онда мұндағы S – D облысының ауданы, ал m мен М сәйкесінше функциясының осы облыстағы ең кіші және ең үлкен мәндері.

Е к і е с е л і и н т е г р а л д ы е с е п т е у.

Интегралдау облысы берілу пішіні (тұрпаты) бойынша екі түрге бөлінеді:

а) D облысы мен түзулерімен және жатқанда үзіліссіз қисық сызықтармен шектелсін, әрі Оу осіне параллель жүргізілген түзулер осы қисықтардың әрқайсысын тек бір нүктеде қисын (3.1 Сурет).

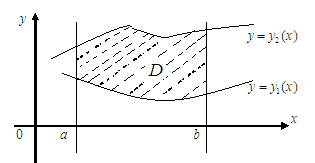
3.1 Сурет

Осындай облыс үшін екі еселі интеграл келесі формуламен есептелінеді:

мұнда алдымен ішкі интегралы есептелінеді, бұл жағдайда х айнымалысы тұрақты деп саналады.

б) D облысы мен түзулерімен пен жатқанда үзіліссіз қисық сызықтарымен шектелсін, әрі Ох осіне параллель жүргізілген түзулер осы қисықтардың әрқайсысын тек бір нүктеде қисын (3.2 Сурет).

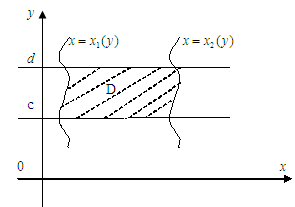
3.2 Сурет

Осындай облыс үшін қос интеграл келесі формуламен есептелінеді:

мұнда алдымен ішкі интегралы есептелінеді, бұл жағдайда у айнымалысы тұрақты деп саналады.

Берілген формулалардың оң жақтары қос интегралдар деп аталады.

317. интегралын есептеу керек, мұнда D облысы тіктөртбұрыш:

Шешуі. ▲

318. интегралын есептеу керек, мұндағы D облысы квадрат:

Шешуі.

▲

319. интегралын есептеу керек.

Шешуі.

▲

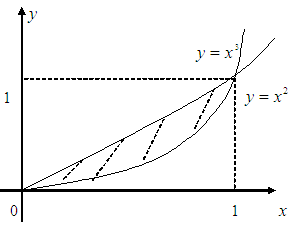
320. интегралын есептеу керек, мұндағы D облысы параболаларымен шектелген.

Шешуі. D облысын сызайық. және параболаларының қиылысу нүктелері және болады (3.3 Сурет).

болғандықтан