
- •Математика 2 Есептер мен жаттығулар
- •Isbn 978-601-266-055-7
- •1 Көп аЙнымалылы функция
- •1.1 Көп айнымалылы функцияның анықталу облысы
- •1.2 Көп айнымалылы функцияның туындылары мен дифференциалдары
- •1.3 Бетке жүргізілген жанама жазықтық және нормаль түзу
- •1.4 Екі айнымалылы функцияның экстремумы
- •1.1 Сурет
- •2 Дифференциалдық теңдеулер
- •2.1 Бірінші ретті дифференциалдық теңдеулер
- •2 Сурет
- •2.2 Жоғарғы ретті дифференциалдық теңдеулер
- •1. Кейбір реті төмендетілетін дифференциалдық теңдеулер.
- •2.3 Дифференциалдық теңдеулер жүйесі
- •3 Қос интеграл
- •3.1 Тік бұрышты координаттар жүйесіндегі қос интегралдар
- •3.1 Сурет
- •3.2 Сурет
- •3.3 Сурет
- •3.4 Сурет
- •3.5 Сурет
- •3.6 Сурет
- •3.2 Қос интегралда айнымалыларды алмастыру
- •3.7 Сурет
- •3.3 Қос интегралдың қолданылуы
- •3.9 Сурет
- •3.10 Сурет
- •3.11 Сурет
- •3.13 Сурет
- •3.14 Сурет
- •3.15 Сурет
- •4 Үштік интегралдар
- •4.1 Сурет
- •4.2 Сурет
- •4.3 Сурет
- •4.4 Сурет
- •4.6 Сурет
- •5 Қисық сызықты және беттік интегралдар
- •5.1 Доға ұзындығы және координаттар бойынша қисық сызықты интегралдар
- •5.2 Беттік интегралдар
- •6 Өріс теориясының элементтері
- •5.3 Сурет
2.3 Дифференциалдық теңдеулер жүйесі
1. Бірінші ретті дифференциалдық теңдеулер жүйесі. Төменде берілген теңдеулер жүйесі:
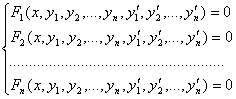
бірінші ретті дифференциалдық теңдеулер жүйесі деп аталады, мұндағы х-тәуелсіз айнымалы, у1, у2,…,уn – ізделінді функциялар.
Егер жүйе ізделінді функциялардың туындылары арқылы шешілген болса, яғни :
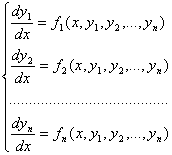
онда нормальдық жүйе деп аталады.
Дифференциалдық теңдеулер жүйесінің жалпы шешімі деп теңдеулер жүйесін теңбе-теңдікке айналдыратын
![]() ,
,
![]() ,
…
,
…
![]()
функциялар жиынтығын айтады.
2. Тұрақты коэффициентті сызықтық дифференциалдық теңдеулер жүйесі. Дифференциалдық теңдеулер жүйесін қарастырғанда 3 теңдеуден тұратын (n=3) жүйемен шектелейік. Төменде айтылғандардың барлығы кез келген ретті жүйе үшін де орындалады.
Тұрақты коэффициентті нормальдық дифференциалдық теңдеулер жүйесі сызықтық біртекті делінеді, егер оны келесі түрде жазу мүмкін болса:

Жүйе
шешімдері:
![]() түрінде ізделінеді. Келесі анықтауышты
есептейміз:
түрінде ізделінеді. Келесі анықтауышты
есептейміз:
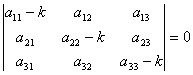
Анықтауышты есептеу нәтижесінде k-ға қатысты үшінші дәрежелі теңдеу аламыз. Бұл теңдеу сипаттамалық (характеристикалық) теңдеу деп аталады және оның k1 , k2, , k3. үш түбірі болады. Оның әрқайсысына берілген жүйенің нөлден өзге шешімі сәйкес келеді:
![]()
![]()
![]()
Бұл шешімдердің сызықтық комбинациясы берілген сызықтық біртекті жүйенің шешімі болады:
![]()
![]()
![]()
294. Жүйенің шешімін табу керек:
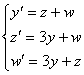
Шешуі. Сипаттамалық теңдеу құрастырайық:
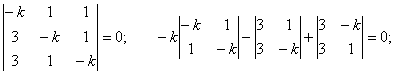
![]()
1) k = -1.
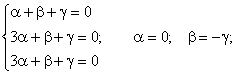
Егер
= 1 десек, онда бұл жағдайда шешімдер:
![]()
2) k2 = -2.
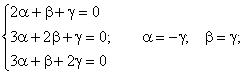
Егер
= 1
десек,
онда:
![]()
3) k3 = 3.
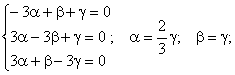
Егер
= 3
десек,
онда:
![]()
Жалпы шешім:
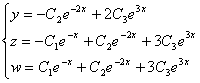 .
▲
.
▲
295. Жүйенің жалпы шешімін табу керек:
![]()
Шешуі. Сипаттамалық теңдеу құрастырайық:
![]()
![]()
Теңдеулер жүйесін шешейік:
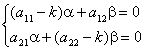
k1 үшін:

![]() делік
(кез
келген мән қоюға болады),
сонда:
делік
(кез
келген мән қоюға болады),
сонда:
![]()
k2 үшін :
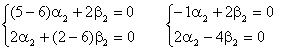
![]() делік
(кез келген мән қоюға болады), сонда:
делік
(кез келген мән қоюға болады), сонда:
![]() Жүйенің
жалпы шешімі:
Жүйенің
жалпы шешімі:
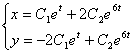 .
▲
.
▲
Бұл мысалды басқа тәсілмен шығаруға болады:
Шешуі.
Бірінші теңдеуді дифференциалдаймыз:
![]()
Бұл өрнекке екінші теңдеудегі туындыны у =2x + 2y қоямыз.
![]()
Оған бірінші теңдеуден у тауып қоямыз:
![]()
![]()
![]()
![]()
![]()
![]()
![]() деп
белгілей отырып,
жүйе
шешімін аламыз:
деп
белгілей отырып,
жүйе
шешімін аламыз:
▲
296. Жүйенің жалпы шешімін табу керек:
![]()
Шешуі.
Бұл жүйе жоғарыда қаралған жүйеден
басқа текті, себебі біртекті
емес
(теңдеуде х-тәуелсіз аргумент бар). Шешу
үшін бірінші теңдеуді х бойынша
дифференциалдаймыз:
![]()
Екінші
теңдеудегі z’
алмастырсақ, онда:
![]() .
.
Бірінші
теңдеуден z
–ті тауып осыған қойсақ, онда:
![]()
Енді алынған екінші ретті дифференциалдық теңдеуді шешейік:
![]()
Біртекті
теңдеудің жалпы шешімі:
![]()
Енді біртекті емес теңдеудің дара шешімін табайық:
![]()
![]()
![]()
Біртекті емес теңдеудің жалпы шешімі:
![]()
Алынған нәтижені жүйенің бірінші теңдеуіне қоямыз:
![]() ▲
▲
Теңдеулер жүйесінің (сипаттамалық теңдеулерін құру арқылы) жалпы шешімін табу керек.
297.
![]() Ж:
Ж:
![]()
298.![]() Ж:
Ж:
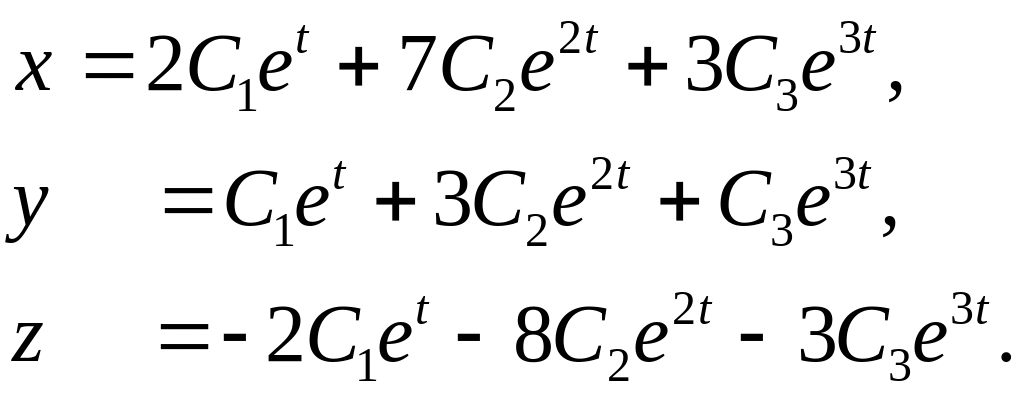
299.
![]() Ж:
Ж:
![]()
300.
![]() Ж:
Ж:

301.
![]() Ж:
Ж:
![]()
302.
![]() Ж:
Ж:
![]()
303.
![]() Ж:
Ж:
![]()
304.
![]() Ж:
Ж:
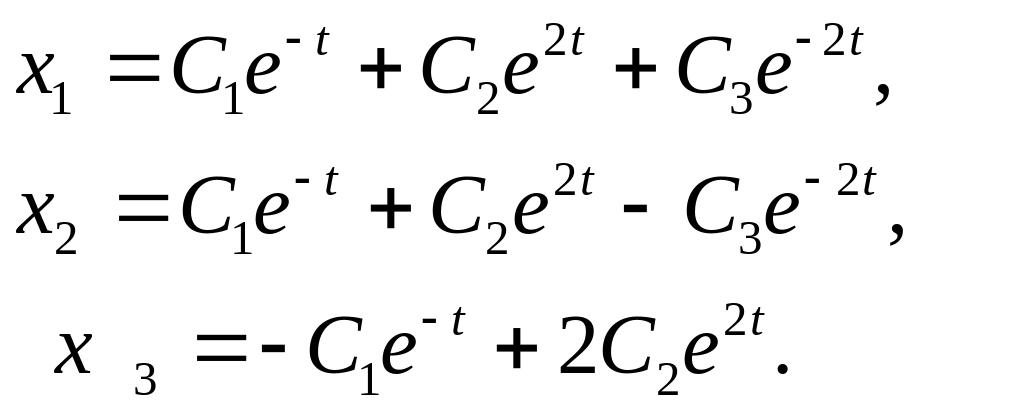
305.
![]() Ж:
Ж:
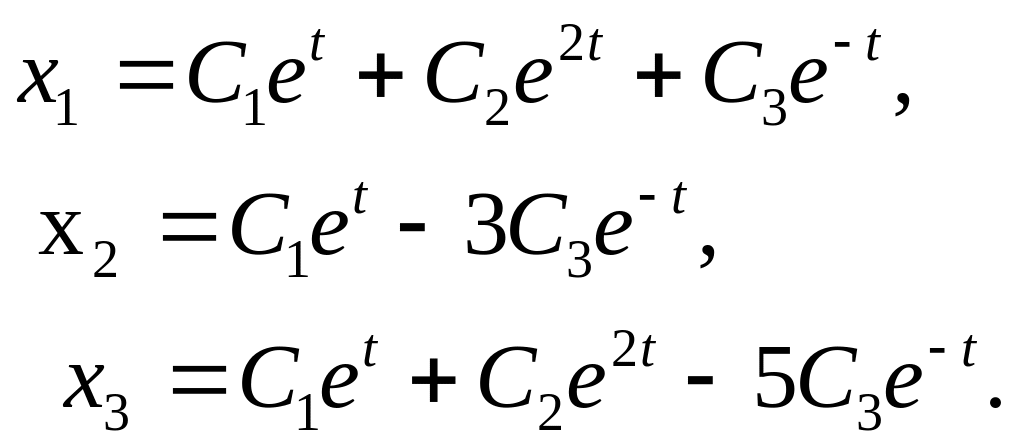
306.
![]() Ж:
Ж:
![]()
Дифференциалдық теңдеулер жүйесін белгісіздерді біртіндеп жою әдісі бойынша шешу керек:
307.![]()
![]() Ж:
Ж:
![]()
308.![]() Ж:
Ж:
![]()
309.
![]() Ж:
Ж:
![]()
310.
![]() Ж:
Ж:
![]()
311.
![]()
![]() Ж:
Ж:

312.
![]()
![]() Ж:
Ж:
![]()
313.
![]() Ж:
Ж:

314.
![]() Ж:
Ж:
![]()
315.
![]() Ж:
Ж:
![]()
316.
![]() Ж:
Ж:
![]()
