2 Сурет

Шешуі: S_трап= екені белгілі, мұндағы MB=y; OB=x;

OC=BM-DM=BM-CDtgDCM=y-xy^/ болғандықтан, трапеция ауданының формуласынан:

а²= х(у+у-ху^/) немесе

- сызықтық біртекті емес дифференциалдық теңдеу аламыз.

Оның шешімін Бернулли әдісімен табайық, яғни алмастыруын жасайық. Теңдеуге апарып қойсақ:

1)

2)

3) - сызықтық біртекті емес дифференциалдық теңдеудің жалпы шешімі, у(а)=а болғандықтан:

- ізделінді қисықтың теңдеуі. ▲

197. - Бернулли теңдеуін шешу керек.

Шешуі:

Алынған сызықтық дифференциалдық теңдеуді шешу үшін тұрақтыны вариациялау әдісін қолданамыз.

немесе

-біртекті сызықтық дифференциалдық теңдеу.

Енді тұрақты с-ны қандайда бір х-қа тәуелді функция деп аламыз, яғни

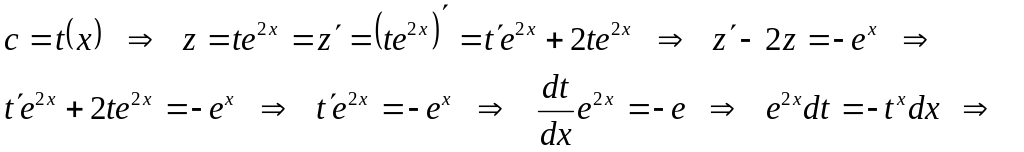
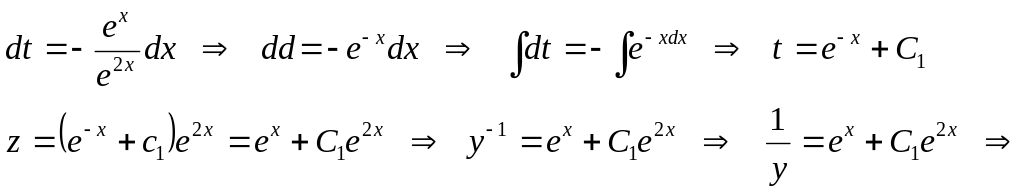
- Бернулли теңдеуінің жалпы шешімі. ▲

6. Толық дифференциалды теңдеулер. Егер теңдеуі шартын қанағаттандырса, яғни теңдеудің сол жағы қайсыбір функциясының дифференциалы болса, онда ол толық дифференциалды теңдеу деп аталады.

Егер теңдеудің сол жағы қайсыбір функциясының толық дифференциалы емес болса, яғни

онда теңдеудің барлық мүшесін оған көбейткенде толық дифференциалды теңдеуге айналатындай, функциясынын табуға болады. Сондағы алынған теңдеудің шешімі бастапқы берілген теңдеудің шешімімен бірдей болады. Бұл функциясы интегралдаушы көбейткіш деп аталады.

1) 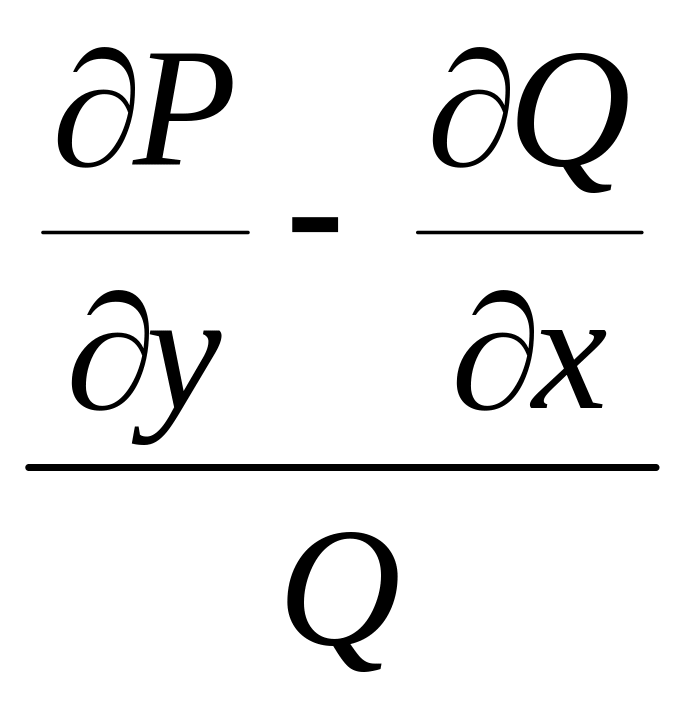функциясы тек х-тен тəуелді болса, оны М(х) деп белгілесек, онда интегралдаушы көбейткіш функциясы болады.

2) функциясы тек у-тен тəуелді болса, оны М(у) деп белгілесек, онда интегралдаушы көбейткіш функциясы түрінде алынады.

198. дифференциалдық теңдеудің жалпы интегралын табу керек.

Шешуі: Мұнда

яғни толық дифференциалды теңдеу болады 

Толық дифференциал

екені белгілі. Сондықтан

.

Олай болса, немесе - жалпы интеграл. ▲

199. ydx − xdy + ln хdx = 0 теңдеуінің жалпы интегралын табу керек.

Шешуі: (у + lnx)dx − xdy = 0 , мұндағы Р(х, y)= у + lnx , Q(х, y)= − х

, яғни

тек х-тен тəуелді, демек интегралдаушы көбейткішті өрнегімен табамыз:

(у + lnx)dx − xdy = 0

Сонымен (у + lnx)dx − dy = 0 теңдеуін алдық, мұндағы Р(х, y)= (у + lnx) , Q(х, y)= − . Енді дербес туындыларын тексерейік:

ал

, яғни

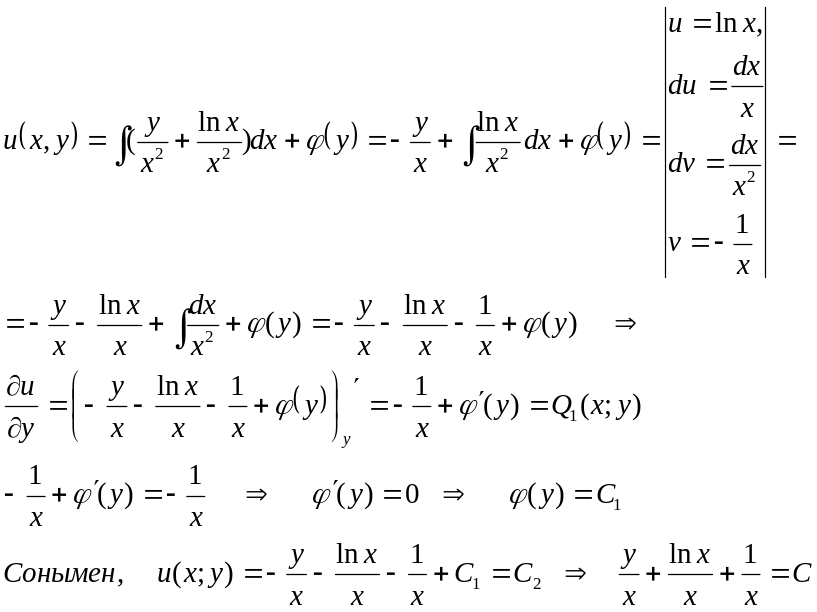
у+lnx+1=Сx - ізделінді жалпы шешім. ▲

Берілген теңдеулер түрлерін анықтап, олардың шешуін екі əдіспен де көрсету керек:

200. Ж:

201. (2x + ye^xy )dx + (1+ xe^xy )dy = 0 Ж: x² + y + e^xy = C

202. sin (x+y) dx+xcos(x+y)(dx+dy) =0 Ж: x sin (x + y)= C

203. dx +(y ³ + ln x)dy = 0 Ж: 4 y ln x + y ⁴ = C

204. 2x(1+ )dx − dy = 0 Ж: x² +2/3 (x² − y)^3/2= C

205. 3х²(1+lny)dx=(2y-x³/y)dy Ж: x ³ + x ³ ln y − y ² = C

206. (2 x ² y ² + 7 )dx + 2 x ³ ydy = 0 Ж: x ³ y ² + 7 x = C

207. 13) (e^y + ye^x +3)dx= (2−xe^y −e^x )dy Ж: xe^y + ye^x +3x−2y =C

208. Ж: x ³ y + x ² − y ² = Cxy

209. Ж: x + arctg = C

210. (2x³−ху² )dx + (2у ³−х ² у)dy = 0 Ж: х⁴-х²у²+у⁴=С

211. е^уdx+(xe^y-2y)dy=0 Ж: хe^y-у²=С

212. yx^y-1dx+x^y lnxdy=0 Ж: х^y =С

Теңдеулердің әуелі интегралдаушы көбейткішін тауып, кейін жалпы шешімін табу керек:

213. (x ² − 3 y ² )dx + 2 xydy = 0 Ж:

214. (sin x + e ^y )dx + cosx dy = 0 Ж: =e^−y; e^−y cosx=C+x

215. (xsiny+ y)dx+(x²cosy+xlnx)dy=0 Ж:

216. (x ² − y )dx + xdy = 0 Ж:

217. 2xtgydx+ (x² − sin y)dy = 0 Ж:

218. dx +(y ³ − ln x)dy = 0 Ж:

219. (1 + xy )dx − xdy = 0 Ж: x ² +

220. (e ^{2 x} − y ² )dx + ydy = 0 Ж: =e^−2х; у²=(С-2х)е^2х

221. (1+3x² sin y)dx− xctgydy= 0 Ж:

222. y ² dx + (yx − 1)dy = 0 Ж:

223. (x²+y)dx-xdy=0 Ж:

224. (x²+y²+2x)dx+2ydy=0 Ж: (x²+y²)e^x=C

225. (xcosy-ysiny)dy+(xsiny+ycosy)dx=0 Ж: (xsiny+ycosy-siny)e^x=C