6 Өріс теориясының элементтері
Егер
кеңістіктің әрбір нүктесіне
скалярлық функцияның мәні сәйкес келсе,
онда оны скалярлық
өріс
дейді.
Мысалы,
егер
функциясы кеңістіктегі V облысының
әрбір нүктесінде температураны анықтаса,
онда оны температураның скалярлық
өрісі
дейді.
скалярлық
өріс бір тек қана бір берілген С мәнін
қабылдайтын нүктелер жиынын деңгейлік
бет дейді, оның теңдеуі
.
Мысалы,
функциясының берілген скалярлық өрісінің
деңгейлік сызығы
шеңберлер тобы болады.
Егер
кеңістіктің әрбір
нүктесінде
векторының анықталған мәні сәйкес келсе, онда векторлық өріс берілді дейді.
Скаляр немесе векторлық өріс t - уақытына байланыссыз болса, онда оны станционарлық, ал байланысты болса, станционарсыз деп атайды.
Векторлық
сызық деп әрбір
нүктесінде бағыты сәйкес
векторымен бағыттас болатын қисық
сызығын айтады. Векторлық сызық
дифференциалдық теңдеулер жүйесімен анықталады.
скалярлық өрістің градиенті деп
векторын
айтады да, қысқаша
символымен белгілейді, мұндағы
- Гамильтон
операторы
немесе набла
дейді.
Өріс градиенті бет деңгейіне жүргізілген нормаль бағытымен функцияның өсу жағына қарай бағытталады және оның өсу жылдамдығының ең үлкен шамасы өріс градиентінің ұзындығының тең, яғни
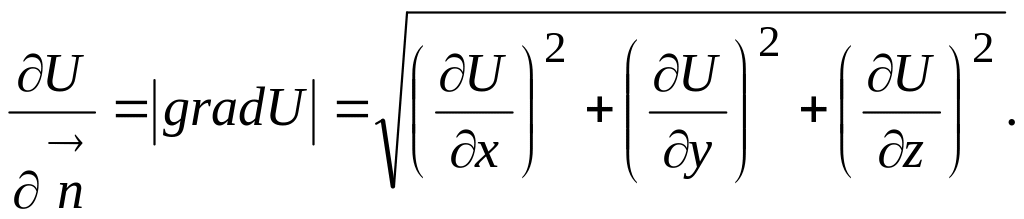
векторлық
өрістің дивергенциясы
деп
скаляр шамасын айтады.
векторлық
өрістің құйыны
(роторы)
деп
векторын айтады.
Бірлік
нормаль бағытындағы
беті бойынша өтетін
векторының ағыны
деп
интегралын айтады.
векторының
L сызығы бойынша алынған сызықты интеграл
формуласымен
анықталады, мұндағы
векторы L қисығына жүргізілген жанама
вектор.
Егер L
қисығы тұйық болса, онда сызықты
интегралды
векторлық өрісінің иірімі
(циркуляциясы)
деп атайды:
Егер L қисығы бетін қоршаған тұйық қисық болса, онда Стокс формуласы орындалады және оның формуласы
немесе
мұндағы векторы бетіне жүргізілген сыртқы нормалы, оның бағытымен қарағанда L контурымен айналу бағыты сағат тіліне қарсы алынады.
Егер V көлемін қоршаған бетін тұйық, ал оған жүргізілген сыртқы нормаль бірлік векторы болса, онда Гаусс-Остраградский формуласы орындалады және оның формуласы
немесе
Егер
өрістің әрбір нүктесінде
болса, онда
векторлық өрісін құбырлық
(соленоидалды) өріс дейді.
Бұл жағдайда кез келген тұйық бет арқылы
өтетін вектор ағыны нөлге тең.
Егер
яғни
болса, онда
векторлық өрісін дәрменді (потенциалды)
өріс дейді, мұндағы U – скалярлық функция.
Берілген бір байланысты облыста
- өрісі дәрменді болу үшін
теңдігінің орындалуы қажетті және
жеткілікті. Бұл жағдайда U – дәрмені
бар және оны
теңдеуімен анықтайды. Егер U – дәрмені бір мәнді функция болса, онда
мұндағы
АВ доғасы L қисығының бойынан алынады,
- кез келген сандар.
Егер векторлық өріс бір мезгілде дәрменді және құбырлы өріс болса, онда
және дәрменді U функциясы гармониялық функция болады, яғни Лаплас теңдеуін қанағаттандырады.
немесе
мұндағы
- Лаплас операторы.
478.
векторлық өрісінің дивергенциясын табу
керек.
Ж:
479.
векторлық өрісінің құйының (роторын)
табу керек.
Шешуі.
▲
480. Стокс
формуласының көмегімен
векторлық өрісінің MNP
үшбұрыш контуры бойынша иірімін
(циркуляциясын) табу керек, мұндағы
Шешуі.
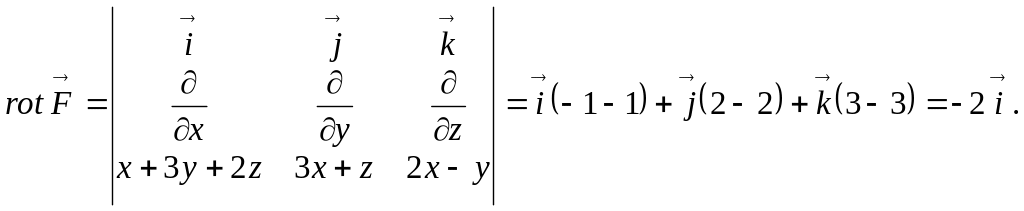
Стокс
формуласы бойынша
MNP
үшбұрышынан тұратын L контуры
жазықтығында жатады, осыдан
▲
481. Стокс
формуласының көмегімен
векторлық өрісінің АВС үшбұрыш контуры
бойынша иірімін (циркуляциясын) табу
керек, мұндағы
Ж:
1.
482. Стокс
формуласының көмегімен
векторлық өрісінің
шеңбері бойынша иірімін (циркуляциясын)
табу керек. Ж:
483.
векторлық өрісі дәрменді (потенциалды)
немесе құбырлы (соленоидалды) бола ма
тексеру керек. Дәрменді өріс болған
жағдайда оны дәрменін (потенциалын)
табу керек.
Шешуі. Векторлық өрістің дәрменділігін тексерейік:
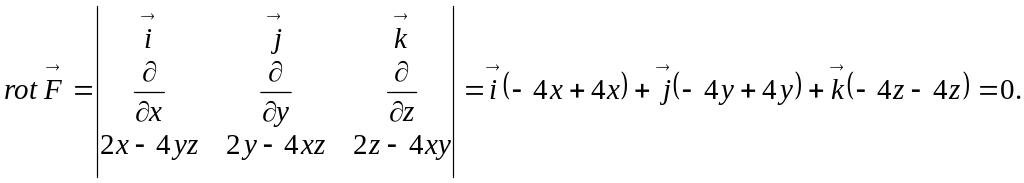
векторлық өрісі дәрменді. Енді өрістің дәрменін табайық.
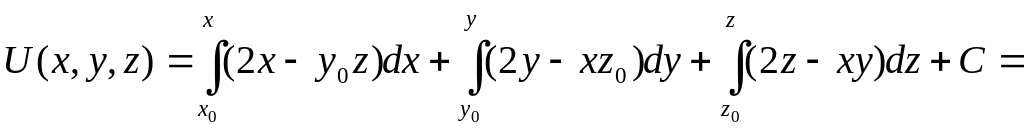
деп
алсақ, онда
Енді
өріс құбырлы бола ма, тексерейік:
Берілген өріс құбырлы емес. ▲
өрісі дәрменді немесе құбырлы
өріс бола ма, тексеру керек. Дәрменді
өріс болған жағдайда дәрменін табу
керек.
484.
Ж: Өріс
дәрменді, бірақ құбырлы емес
485.
Ж:
Өріс
әрі дәрменді, әрі құбырлы (гармоникалық
өріс)
486.
Ж:
Өріс
дәрменді емес, бірақ құбырлы.
өрісі және
жазықтығы мен координат жазықтықтарымен
шектелген пирамида
беті берілсін. Гаусс-Остроградский
формуласының көмегімен
өрісінің ағынын есептеу керек.
487.
Шешуі.
Сонымен, 5.3 Сурет бойынша интегралдар шектерін қояйық:
▲