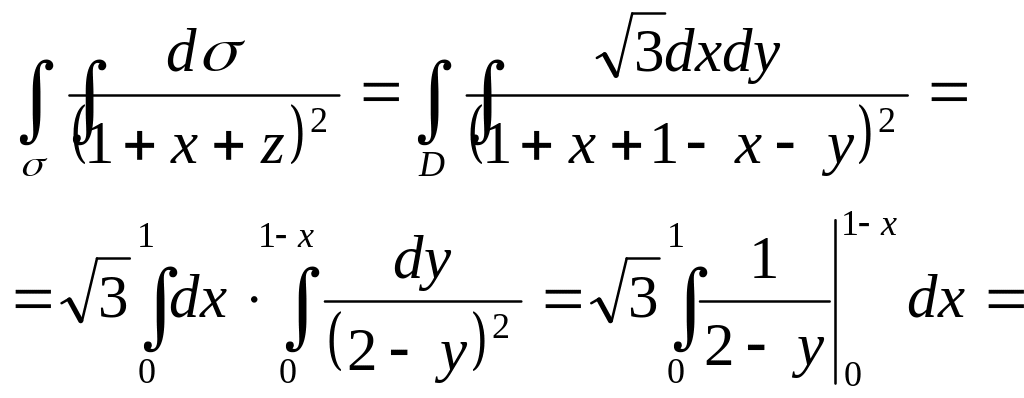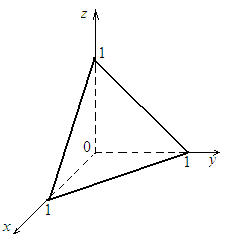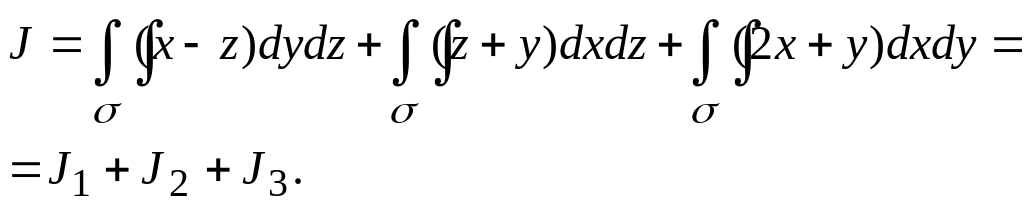- •Математика 2 Есептер мен жаттығулар
- •Isbn 978-601-266-055-7
- •1 Көп аЙнымалылы функция
- •1.1 Көп айнымалылы функцияның анықталу облысы
- •1.2 Көп айнымалылы функцияның туындылары мен дифференциалдары
- •1.3 Бетке жүргізілген жанама жазықтық және нормаль түзу
- •1.4 Екі айнымалылы функцияның экстремумы
- •1.1 Сурет
- •2 Дифференциалдық теңдеулер
- •2.1 Бірінші ретті дифференциалдық теңдеулер
- •2 Сурет
- •2.2 Жоғарғы ретті дифференциалдық теңдеулер
- •1. Кейбір реті төмендетілетін дифференциалдық теңдеулер.
- •2.3 Дифференциалдық теңдеулер жүйесі
- •3 Қос интеграл
- •3.1 Тік бұрышты координаттар жүйесіндегі қос интегралдар
- •3.1 Сурет
- •3.2 Сурет
- •3.3 Сурет
- •3.4 Сурет
- •3.5 Сурет
- •3.6 Сурет
- •3.2 Қос интегралда айнымалыларды алмастыру
- •3.7 Сурет
- •3.3 Қос интегралдың қолданылуы
- •3.9 Сурет
- •3.10 Сурет
- •3.11 Сурет
- •3.13 Сурет
- •3.14 Сурет
- •3.15 Сурет
- •4 Үштік интегралдар
- •4.1 Сурет
- •4.2 Сурет
- •4.3 Сурет
- •4.4 Сурет
- •4.6 Сурет
- •5 Қисық сызықты және беттік интегралдар
- •5.1 Доға ұзындығы және координаттар бойынша қисық сызықты интегралдар
- •5.2 Беттік интегралдар
- •6 Өріс теориясының элементтері
- •5.3 Сурет
5.2 Беттік интегралдар
1. Бет
ауданы бойынша беттік интегралдар (І
текті беттік интегралдар).
![]() үзіліссіз функциясы болсын және
үзіліссіз функциясы болсын және
![]() формуласымен
беті берілсін.
Бет
ауданы бойынша беттік интеграл ( не І
текті
беттік интеграл)
деп
формуласымен
беті берілсін.
Бет
ауданы бойынша беттік интеграл ( не І
текті
беттік интеграл)
деп
![]()
мұндағы
![]() -
бетінің k-ші элементінің ауданы,
-
бетінің k-ші элементінің ауданы,
![]() нүктесі осы элементке тиісті,
нүктесі осы элементке тиісті,
![]() функциясы
бетінің әрбір нүктесінде анықталады.
функциясы
бетінің әрбір нүктесінде анықталады.
Егер бет теңдеуімен берілсе, онда І текті беттік интеграл
![]()
формуласымен есептеледі.
468.
![]() интегралын есептеу керек, мұндағы
интегралын есептеу керек, мұндағы
![]() :
:
![]() жазықтығының І октанттағы бөлігі.
жазықтығының І октанттағы бөлігі.
Шешуі. Жазықтық
теңдеуін түрлендірейік:
![]() .
Бұдан
.
Бұдан
![]()
![]() .
.
бетінің Оху жазықтығына проекциясы х+у=1, x=0, y=0 түзулерімен шектелген D үшбұрышы болады (5.1 Сурет). Осы үшбұрышта х 0-ден 1-ге дейін өзгереді.
|
5.1 Сурет |
▲
469.
![]() интегралын есептеу керек, мұндағы
беті
интегралын есептеу керек, мұндағы
беті
![]() конусының
конусының
![]() және
және
![]() жазықтықтарының арасындағы бөлігі.
жазықтықтарының арасындағы бөлігі.
Шешуі.
![]() ,
,
![]()
Сонда
берілген интеграл
![]()
Интегралдау
облысы D:
![]() дөңгелегі болғандықтан
дөңгелегі болғандықтан
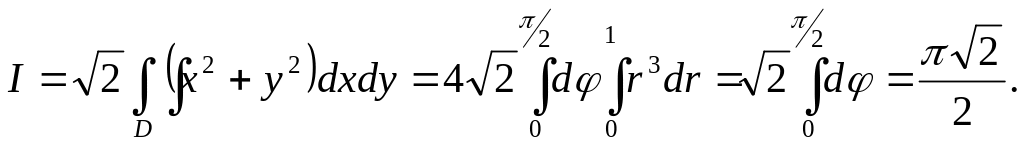 .
▲
.
▲
470.
![]() бетінің
бетінің
![]() цилиндрімен шектелген бөлігінің ауданын
есептеу керек.
цилиндрімен шектелген бөлігінің ауданын
есептеу керек.
Шешуі.
![]() ,
бұдан
,
бұдан
![]() ,
ал
,
ал
![]()
![]() .
.
![]() :
:
![]() дөңгелегі болады. Полярлық координаттар
жүйесіне көшсек:
дөңгелегі болады. Полярлық координаттар
жүйесіне көшсек:
![]() ,
,
онда
![]() .
▲
.
▲
471.
![]() интегралын есептеу керек, мұндағы
беті:
интегралын есептеу керек, мұндағы
беті:
![]() жазықтығының бірінші октанттағы
бөлігі. Ж:
жазықтығының бірінші октанттағы
бөлігі. Ж:
![]() .
.
472.
![]() интегралын есептеу керек, мұндағы
беті:
интегралын есептеу керек, мұндағы
беті:
![]() параболоидының
параболоидының
![]() жазықтығымен қиғандағы бөлігі. Ж:
жазықтығымен қиғандағы бөлігі. Ж:
![]() .
.
473.
![]() интегралын есептеу керек, мұндағы
беті:
интегралын есептеу керек, мұндағы
беті:
![]() параболоидының
параболоидының
![]() және
және
![]() жазықтықтарымен қиғандағы бөлігі.
жазықтықтарымен қиғандағы бөлігі.
Ж:
![]()
2.
Координаттар бойынша беттік интегралдар
(ІІ текті беттік интегралдар).
![]() -үзіліссіз функциялары, L
сызығымен шектелген
беті және
бетінің әрбір
-үзіліссіз функциялары, L
сызығымен шектелген
беті және
бетінің әрбір
![]() нүктесінде оң бағытта бағытталған
нүктесінде оң бағытта бағытталған
![]() нормалі (бірлік векторы) берілсе, онда
ІІ
текті беттік интеграл
нормалі (бірлік векторы) берілсе, онда
ІІ
текті беттік интеграл
![]()
өрнектеледі.
Егер
беті
![]() теңдеуімен айқын емес түрде берілсе,
онда нормальдің бағыттаушы косинустары
теңдеуімен айқын емес түрде берілсе,
онда нормальдің бағыттаушы косинустары
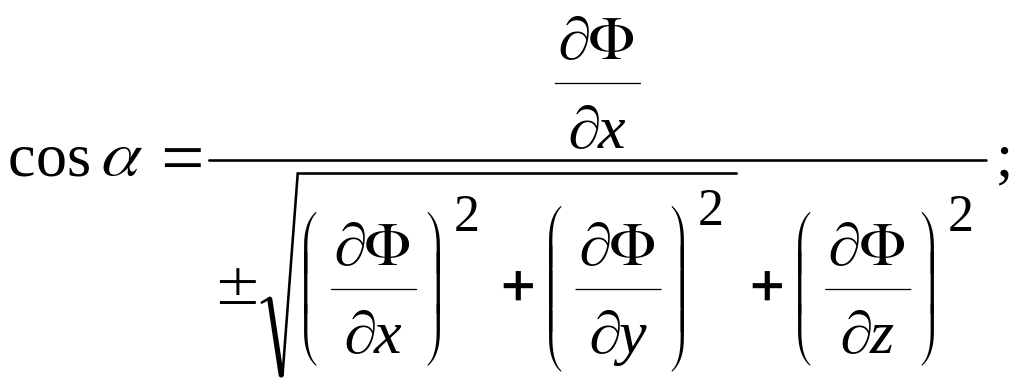
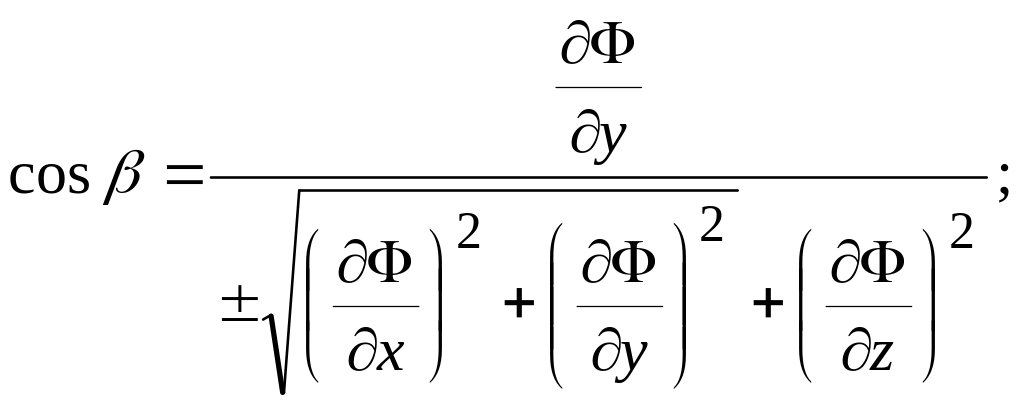
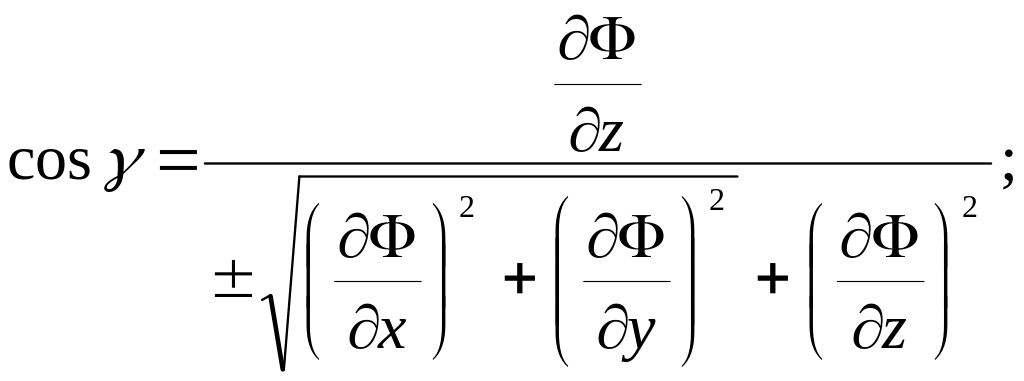
формулаларымен
анықталады, мұндағы таңба
бетінің
![]() нормалінің бағытына байланысты
анықталады.
нормалінің бағытына байланысты
анықталады.
Егер
беті
![]() немесе
немесе
![]() немесе
немесе
![]() формуласымен берілсе және
бетінің
формуласымен берілсе және
бетінің
![]() жазықтықтарындағы проекцияларын сәйкес
жазықтықтарындағы проекцияларын сәйкес
![]() деп белгілесек, онда ІІ текті беттік
интеграл
деп белгілесек, онда ІІ текті беттік
интеграл
![]()
![]()
![]()
формулаларымен есептеледі.
474.
![]() интегралын есептеу керек, мұндағы
беті
интегралын есептеу керек, мұндағы
беті
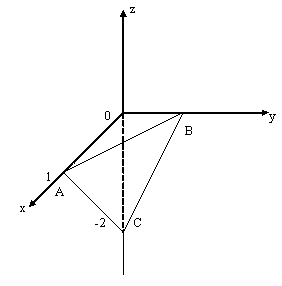
![]() жазықтығының координат жазықтықтарымен
қиғандағы бөлігі, нормаль бағыты Ох
осімен сүйір бұрыш жасайды (5.2 Сурет).
жазықтығының координат жазықтықтарымен
қиғандағы бөлігі, нормаль бағыты Ох
осімен сүйір бұрыш жасайды (5.2 Сурет).
5.2 Сурет |
Шешуі.
|
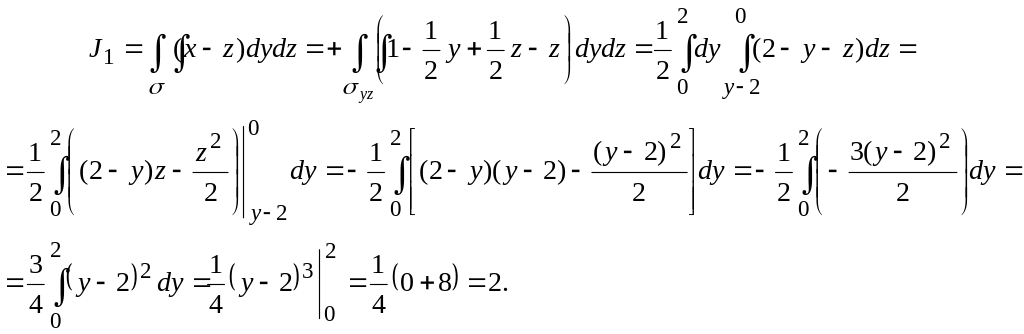
![]() интегралын
есептейік.
интегралын
есептейік.
![]()
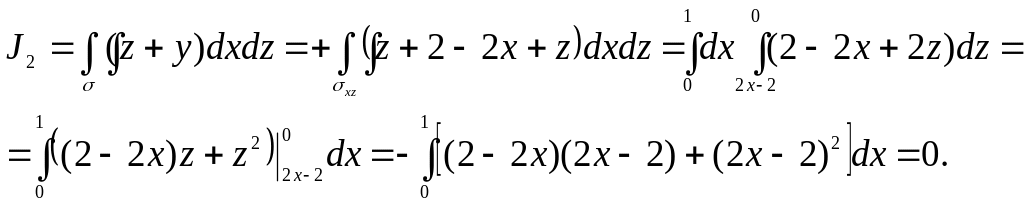
![]() интегралын
есептейік.
интегралын
есептейік.
![]()
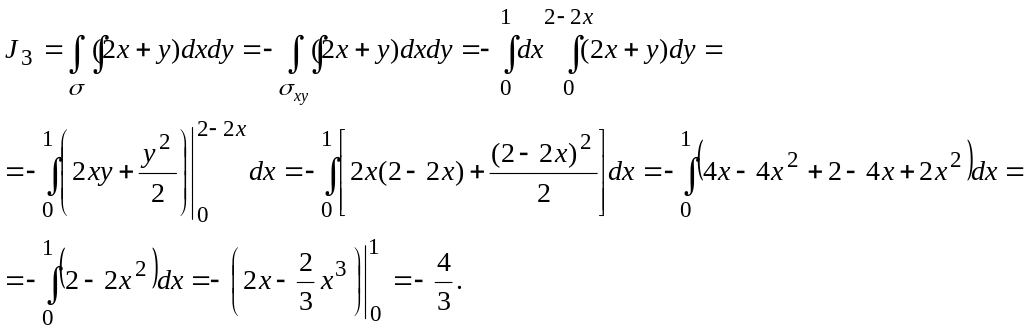
Сонымен
![]() ▲
▲
475.
![]() интегралын есептеу керек, мұндағы
беті
интегралын есептеу керек, мұндағы
беті
![]() жазықтығының координаттар жазықтығымен
қиғандағы бөлігі.
жазықтығының координаттар жазықтығымен
қиғандағы бөлігі.
Ж: 21.
476.
![]() интегралын есептеу керек, мұндағы
беті
интегралын есептеу керек, мұндағы
беті
![]() эллипсоидының бірінші октанттағы
бөлігі. Ж:
эллипсоидының бірінші октанттағы
бөлігі. Ж:
![]()
477.
![]() интегралын есептеу керек, мұндағы
беті
интегралын есептеу керек, мұндағы
беті
![]() жазықтығының бірінші октанттағы бөлігі.
Ж:
жазықтығының бірінші октанттағы бөлігі.
Ж:
![]()