5 Қисық сызықты және беттік интегралдар

5.1 Доға ұзындығы және координаттар бойынша қисық сызықты интегралдар

1. Доға ұзындығы бойынша қисық сызықты интегралдар (І текті қисық сызықты интегралдар). функциясы АВ доғасының нүктелерінде анықталған және үзіліссіз болсын.

АВ доғасын кез келген жолмен нүктелерімен n элементар доғаларға бөлейік. доғасының ұзындығы болсын. Әр элементар доғадан кез келген бір нүктеден таңдап алып, функциясының мәндерін сәйкес аудандарына көбейтейік . функциясы үшін АВ доға ұзындығы бойынша интегралдық қосынды деп

қосындысын айтады.

Доға ұзындығы бойынша (не І текті) қисық сызықты интеграл деп интегралдық қосындының -дағы шегін айтады.

мұндағы dS – доға дифференциалы.

а) Егер АВ қисығы формуласымен берілсе, онда І текті қисық сызықты интеграл

формуласымен есептеледі.

ә) Егер АВ қисығы параметрлік теңдеумен берілсе онда

Кеңістікте үш айнымалылы функциясының І текті қисық сызықты интегралы берілсін. Егер кеңістіктегі қисық теңдеуімен берілсе, онда

Егер болса, онда - І текті қисық сызықты интегралы тығыздығы болатын АВ қисығының массасына тең болады (физикалық мағынасы).

Егер болса, онда - І текті қисық сызықты интегралы жасаушылары Oz осіне параллель болатын, жоғарыдан қисығымен, төменнен Оху жазықтығымен шектелген цилиндрлік беттің ауданына тең болады (геометриялық мағынасы).

І т е к т і қ и с ы қ с ы з ы қ т ы и н т е г р а л д ы ң н е г і з г і қ а с и е т т е р і:

1⁰. І текті қисық сызықты интеграл интегралдау жолының бағытына тәуелсіз болады, яғни

2⁰.

3⁰.

4⁰. Егер С нүктесі АВ қисығында жатса, онда

428. интегралын есептеу керек, мұндағы АВ – түзуінің нүктесінен нүктесіне дейінгі бөлігі.

Шешуі. АВ түзуінің теңдеуі болады.

Осыдан ▲

429. интегралын есепте, егер доғасы,

Шешуі.

▲

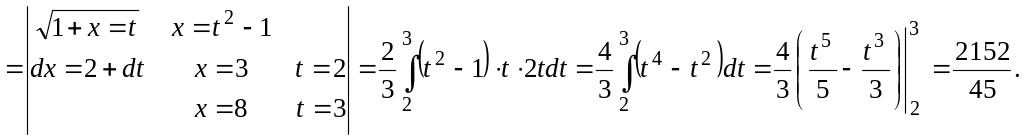430. интегралын есепте, мұндағы үшбұрышының контуры

Шешуі.

АВ теңдеуі: ОВ теңдеуі: ОА теңдеуі: ▲

431. интегралын есептеу керек, мұндағы ОА – түзуінің нүктесі мен нүктесінің арасындағы бөлігі. Ж:

432. интегралын есептеу керек, мұндағы АВ: теңдеуімен берілген жарты кубтық параболаның доғасы, нүктесінен нүктесіне дейін. Ж:

433. интегралын есептеу керек, мұндағы АВ - шеңбердің бөлігі. Ж:

434. интегралын есептеу керек, мұндағы L: шеңбердің контуры. Ж:

435. интегралын есептеу керек, мұндағы L: винттік сызығының бірінші айналымы.

Ж:

436. интегралын есептеу керек, мұндағы шеңберінің бөлігі. Ж:

437. интегралын есептеу керек, мұндағы түзуінің нүктесінен нүктесіне дейінгі бөлігі. Ж:

2. Координаттар бойынша қисық сызықты интегралдар (ІІ текті қисық сызықты интегралдар). және функциялары АВ доғасының нүктелерінде үзіліссіз болсын.

функциялары үшін координаттар бойынша интегралдық қосынды деп

қосындысын айтады.

Координаттар бойынша (не ІІ текті) қисық сызықты интеграл деп интегралдық қосындының және -дағы шегін айтады:

.

ІІ текті қисық сызықты интеграл - айнымалы күштің АВ қисық сызықты жолмен жүрген жұмысы болады (механикалық мағынасы).

ІІ т е к т і қ и с ы қ с ы з ы қ т ы и н т е г р а л д ы ң н е г і з г і қ а с и е т т е р і:

1. ІІ текті қисық сызықты интеграл интегралдау жолының бағытын ауыстырғанда таңбасын қарама-қарсыға өзгертеді, яғни

- .

2. .

(Қалған қасиеттері І текті қисық сызықты интегралдың қасиеттеріне ұқсас болады).

а) Егер АВ қисығы , формуласымен берілсе, онда ІІ текті қисық сызықты интеграл

.

ә) Егер АВ қисығы параметрлік теңдеумен берілсе, онда

Кеңістікте үш айнымалылы функцияларының ІІ текті қисық сызықты интегралы берілсін. Егер кеңістіктегі қисық теңдеуімен берілсе, онда

Тұйық сызық бойынша ІІ текті қисық сызықты интегралы берілсе, онда интегралдау жолы сағат тіліне қарама-қарсы бағытта алынады (оң бағыт деп саналады).

438. интегралын есептеу керек, мұндағы нүктесінен нүктесіне дейінгі түзудің бөлігі.

Шешуі. АВ түзуінің теңдеуі

немесе болады. , осыдан

▲

439. интегралын есептеу керек, мұндағы АВ: параболасының доғасы, нүктесінен нүктесіне дейін.

Шешуі.

▲

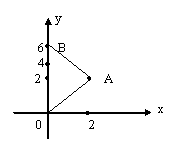
440. интегралын есептеу керек, мұндағы L контуры сағат тіліне қарсы бағыттағы

Шешуі. Интегралдау контурын үшке бөлеміз.

ОА аралығында х 0-ден 2-ге дейін өзгереді. АВ аралығында х 2-ден 0-ге дейін өзгереді,

ВО аралығында у 6-дан 0-ге дейін өзгереді. ,

.

Сонымен,

. ▲

441. интегралын есептеу керек , мұндағы

.

Шешуі.

▲

442. интегралын есептеу керек, мұндағы ОА түзуінің О(0;0) нүктесінен А(2;1) нүктесіне дейінгі бөлігі. Ж: 4/3.

443. интегралын есептеу керек, мұндағы АВ түзуінің

А(2;-2) нүктесінен В(-2; 2) нүктесіне дейінгі бөлігі. Ж: .

444. интегралын есептеу керек, мұндағы L: ОАВ- сынық сызығы, Ж:

445. интегралын есептеу керек, мұндағы L – сағат тіліне қарсы бағыттағы Ох осінен жоғары орналасқан параболасының бөлігі. Ж: 4.

446. интегралын есептеу керек, мұндағы L: түзулерінен құралған тіктөртбұрыш контуры. Ж: 1.

447. интегралын есептеу керек, мұндағы L: шеңберінің бірінші ширегі (сағат тіліне қарсы бағыт бойынша). Ж:

448. интегралын есептеу керек, мұндағы L: параболаларымен шектелген контур (сағат тіліне қарсы бағыт бойынша). Ж:

449. интегралын есептеу керек, мұндағы ОА: шеңберінің бірінші ширегі (сағат тіліне қарсы бағыт бойынша). Ж:

450. интегралын есептеу керек, егер Ж:

3. ІІ текті қисық сызықты интегралдың интегралдау жолына тәуелсіздігі. Функцияны оның толық дифференциалы арқылы табу. функциялары және олардың бірінші ретті дербес туындылары D облысында және осы облыста толығымен жататын С қисық сызығында үзіліссіз болсын.

интегралы интегралдау жолына тәуелсіз болуы үшін шартының орындалуы қажетті және жеткілікті.

Осы шарт орындалғанда D облысында жатқан кез келген L тұйық контуры бойынша алынған қисық сызықты интеграл нөлге тең болады, яғни

.

шарты орындалғанда интеграл астындағы өрнек қандай да бір функциясының толық дифференциалына тең болады, яғни

функциясы (алғашқы функциясы)

немесе

формуласымен табылады, мұндағы кез келген тұрақты сан, ал интегралы, мұндағы

формуласымен есептеледі.

451. интегралын есептеу керек.

Шешуі.

осыдан

Онда

▲

452. болса, алғашқы функциясын табу керек.

Шешуі. деп аламыз. Сонда

▲

453. интегралын есептеу керек. Ж: 20,5.

454. интегралын есептеу керек. Ж:

455. интегралын есептеу керек.

Ж: 198.

алғашқы функциясын оның толық дифференциалы арқылы табу керек.

456. Ж:

457. Ж:

458. Ж:

459. Ж:

4. Грин формуласы. Егер функциялары және дербес туындылары D облысында және оның L шекарасында үзіліссіз болса, онда

болады және оны Грин формуласы дейді, әрі мұнда L контуры бойынша бағыт D облысы сол жақта болатындай етіп таңдап алынады.

460. Грин формуласының көмегімен интегралын есептеу керек, мұндағы L – төбелері болатын тұйық үшбұрыш контуры.

Шешуі.

Сонда мұндағы D облысы -

АВ түзуінің теңдеуі

ВС түзуінің теңдеуі

▲

461. Грин формуласының көмегімен интегралын есептеу керек, мұндағы L: шеңбері.

Шешуі. Сонда

Осыдан

Полярлық координаттар жүйесіне көшеміз:

▲

462. Грин формуласының көмегімен

D облысының L шекарасы бойынша қисық сызықты интегралын қос интегралға түрлендіру керек. Ж:

463. Грин формуласының көмегімен интегралын есептеу керек, мұндағы L: -тіктөртбұрыш контуры. Ж: 8.

5. Ауданды есептеу. Тұйық L сызығымен шектелген фигураның ауданы

формуласымен есептеледі. Мұнда интегралдау L контуры бойынша бағыт D облысы сол жақта болатындай етіп таңдап алынады.

464. астроидымен шектелген фигураның ауданын табу керек.

Шешуі.

Осыдан,

▲

465. эллипсімен шектелген фигураның ауданын табу керек. Ж: .

466. параболаларымен шектелген фигураның ауданын табу керек. Ж:

467. кардиоидамен шектелген фигураның ауданын табу керек. Ж: