4.4 Сурет
Ал тікбұрышты координаттардан
формулаларының
көмегімен
сфералық координаттарға көшкенде
якобиан
болады (4.5 Сурет). Сондықтан
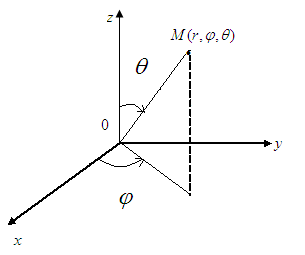
4.5 Сурет
404.
интегралын есептеу керек, мұндағы V
облысы
цилиндрімен және
жазықтықтарымен шектелген.
Шешуі.
Цилиндрлік координаталарға көшейік.
Бұл жағдайда
немесе
Сондықтан
▲
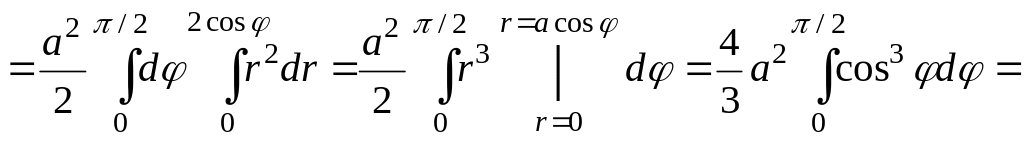
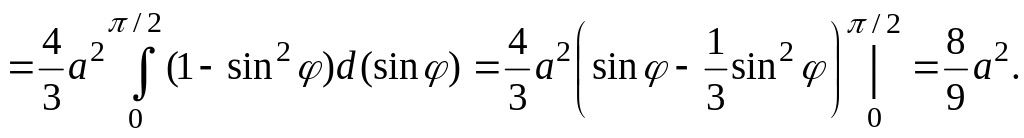405.
интегралын есептеу керек, мұндағы үш
өлшемді V
облысы
шарымен шектелген.
Шешуі.
Сфералық координаттар жүйесіне көшейік.
Бұл жағдайда
Сондықтан
▲
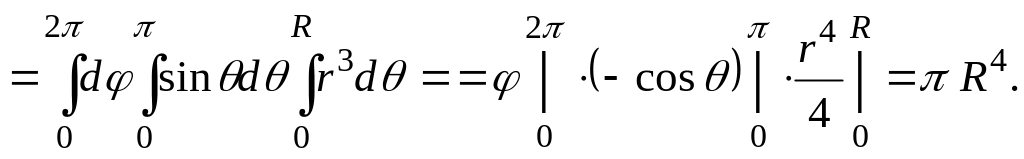406.
интегралын есептеу керек, мұндағы V
денесі
цилиндрімен және
жазықтықтарымен шектелген.
Ж:
407.
интегралын есептеу керек, мұндағы V
денесі
цилиндрімен,
конусымен және
жазықтығымен шектелген. Ж:
408.
интегралын есептеу керек, мұндағы V
денесі
цилиндрімен және
жазықтықтарымен шектелген. Ж:
409.
интегралын есептеу керек, мұндағы V
– шар:
Ж:
410.
интегралын есептеу керек, мұндағы V
– шар:
Ж:
411.
интегралын есептеу керек, мұндағы V
денесі
сферасыен және
жазықтықтарымен шектелген.
Ж:
3. Үштік интегралдың механикада қолданылуы. V денесінің көлемі
формуласымен есептеледі.
Тығыздығы
болатын V
денесінің массасы
,
ал
жазықтықтарына қарағандағы статикалық
моменттері сәйкесінше
формуласымен
есептелінеді. Біртекті дене үшін
Дененің ауырлық центрінің координаттары
формулаларымен анықталады.
осьтеріне
және О
нүктесіне қарағандағы инерция моменттері
(екпіндік қарымдары) сәйкес
формулаларымен есептеледі.
412.
параболоидымен және
жазықтығымен шектелген дененің көлемін
табу керек.
Шешуі.
Берілген дене жоғарыдан
жазықтығымен, ал төменнен
параболоидымен шектелген. Оның
жазықтығындағы проекциясы
теңсіздігімен анықталатын дөңгелек.
Бұл жағдайда цилиндрлік координаттарға
көшсек параболоидтың
болады. Осыдан
▲
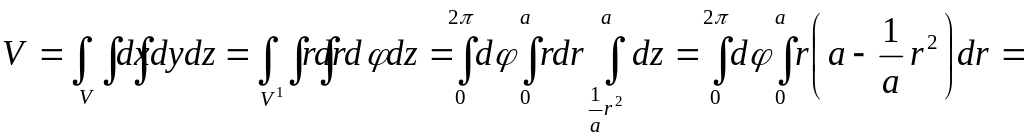
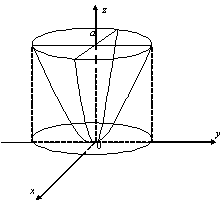
4.6 Сурет
413. Тығыздығы
тұрақты
жарты шарының ауырлық центрінің
координаттарын табу керек.
Шешуі.
Жарты шар симметриялы дене болғандықтан
Дене жоғарыдан
бетімен, төменнен
жазықтығымен шектелген, ал оның Оху
жазықтығындағы проекциясы
дөңгелегі болады.
Сфералық
координаттарға көшсек, онда
болады. Осыдан
.
▲
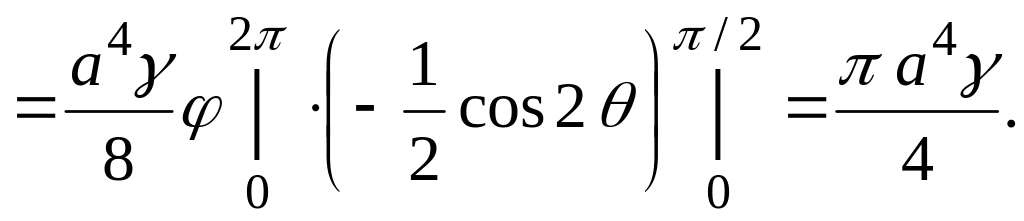
414.
конустық бетімен
жазықтығымен шектелген, дененің
координаттық осьтеріне және бас нүктеге
қарағандағы инерция моменттерін табу
керек
.
Шешуі. Дене жоғарыдан жазықтығымен, төменнен конустық бетімен шектелген. Оның Оху жазықтығындағы проекциясы дөңгелегі болады.
Инерция моменттерін цилиндрлік координаттарға көшу арқылы есептейміз.
▲
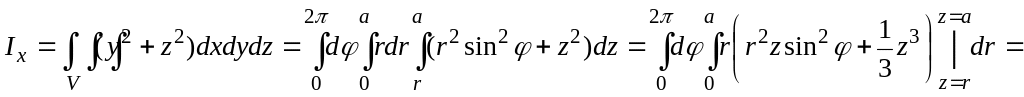
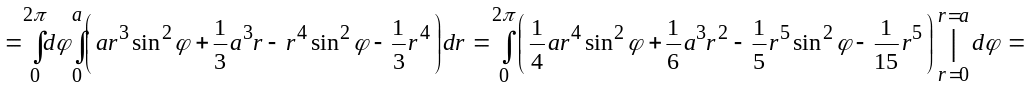
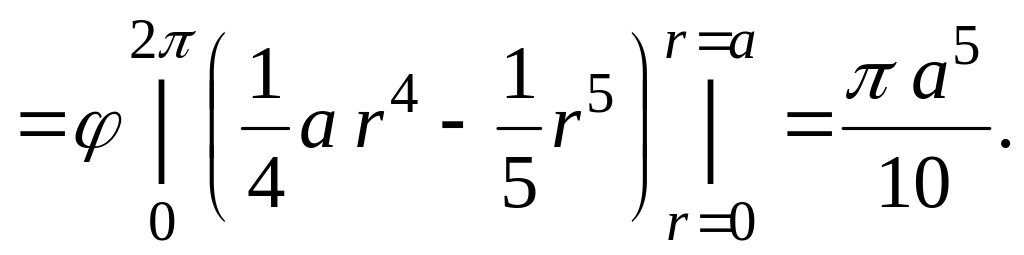
415.
беттерімен шектелген дененің көлемін
табу керек. Ж:
416.
беттерімен шектелген дененің көлемін
табу керек. Ж:
417.
жазықтықтарымен шектелген дененің
көлемін табу керек. Ж:
4,5.
418.
беттерімен шектелген дененің көлемін
табу керек. Ж:
419.
беттерімен шектелген дененің көлемін
табу керек. Ж:
420. Тығыздығы
функциясымен анықталған
параллелипипедінің массасын табу
керек.
Ж:
421.
жазықтықтарымен шектелген, тығыздығы
болатын пирамиданың массасын табу
керек. Ж:
422.
параболоидымен және
жазықтығымен шектелген біртекті дененің
ауырлық центрін табу керек. Ж:
423.
жазықтығымен шектелген біртекті дененің
ауырлық центрін табу керек. Ж:
424.
жазықтықтарымен шектелген дененің
ауырлық центрін табу керек
Ж:
425. Біртекті
шарының координаттық остеріне және
оның бас нүктесіне қарағандағы инерция
моменттерін (екпіндік қарымдарын)
есептеу керек
Ж:
426.
жазықтықтарымен шектелген дененің
координаттық осьтеріне және оның бас
нүктесіне қарағандағы инерция моменттерін
есептеу керек
Ж:
427.
цилиндрімен
және
жазықтықтарымен шектелген дененің
координаттық осьтеріне және оның бас
нүктесіне қарағандағы инерция моменттерін
(екпіндік қарымдарын) есептеу керек
Ж:
