4 Үштік интегралдар
1. Тік
бұрышты координаттар жүйесіндегі үштік
интегралдар.
кеңістігіндегі тұйық
облыста анықталған
функциясы берілсін. Үш өлшемді
облысын кез келген жолмен n
қарапайым облыстарға бөлейік. Осы
қарапайым облыстардың көлемдерін
ал оларға сәйкес диаметрлерін
арқылы белгілейік, мұндағы облыстардың
диаметрі
деп осы облыстың шекарасындағы (бетіндегі)
екі нүктенің ара қашықтықтарының ең
үлкенін айтады.
Әрбір
қарапайым облыстардан кез келген бір
нүктеден таңдап алып, осы нүктелердегі
берілген функциялардың мәндерін сәйкес
көлемдеріне көбейтіп қоссақ
өрнегі шығады. Осы қосынды
функциясының
облысындағы интегралдық
қосындысы
деп аталады.
Егер
осы интегралдық қосындысының
шегі бар және ол шек үш өлшемді облыстың
n
қарапайым облыстарға қалай бөлгенінен
де, әрбір қарапайым облыстардан
нүктесінің қалай алғанынанда тәуелсіз
болса, онда осы шек
функциясының
облысындағы үштік
интегралы
деп аталады да былай белгіленеді:
Егер
үш өлшемді
облысында
болса, онда
үштік интегралы тығыздығы
болатын
денесінің массасына
тең болады (үштік интегралдың физикалық
мағынасы).
Үштік интегралдың негізгі қасиеттері қос интегралдың негізгі қасиеттері сияқты болады.
Интегралдау
облысы
теңсіздіктерімен анықталсын, мұндағы
үзіліссіз функциялар. Осы
облысында
функциясының үштік интегралы
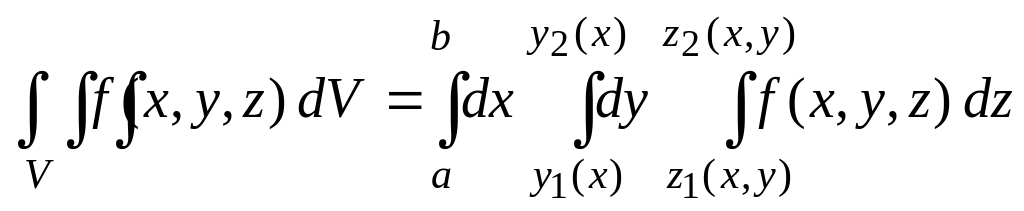
формуласымен анықталады.
395.
интегралын есептеу керек, мұндағы
денесі
теңсіздіктерімен анықталады.
Шешуі.
▲
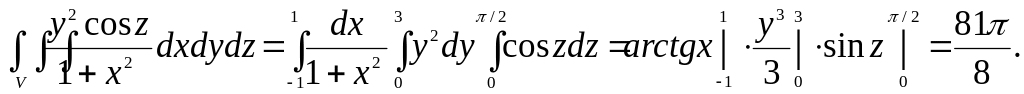396.
интегралын есептеу керек, мұндағы
денесі
теңсіздіктерімен анықталады.
Шешуі.
▲
397.
интегралын есептеу керек, мұндағы үш
өлшемді
денесі координаттар жазықтықтары және
жазықтығымен шектелген (4.1 Сурет).
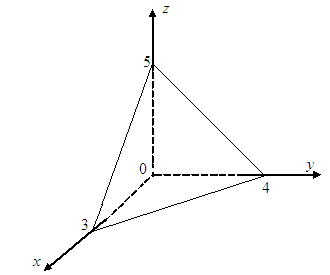
4.1 Сурет
Шешуі.
денесі жоғарыдан
ал төменнен
жазықтығымен шектелген.
денесінің
жазықтығындағы проекциясы
түзулерімен шектелген үшбұрыш. Сонымен
▲
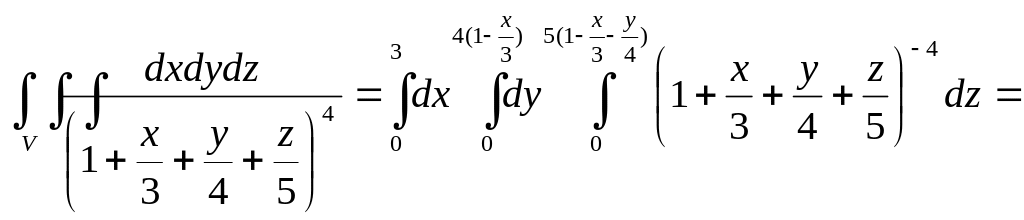
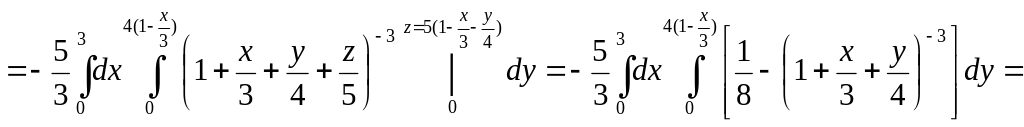
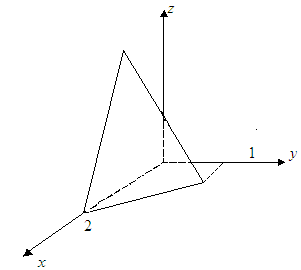
4.2 Сурет
398.
интегралын есептеу керек, мұндағы
денесі
жазықтықтарымен шектелген (4.2 Сурет).
Шешуі.
денесі жоғарыдан
төменнен
жазықтығымен шектелген.
денесінің
жазықтығындағы проекциясы
түзулерімен шектелген, яғни
(4.3
Сурет).
Сонымен
.
▲
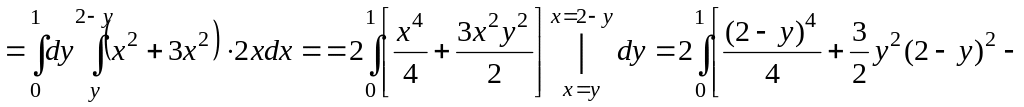
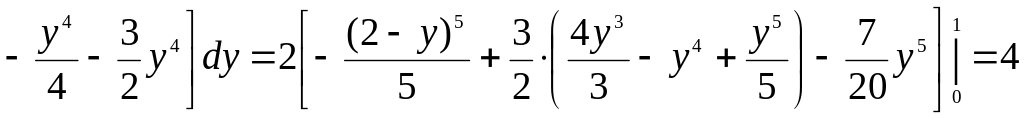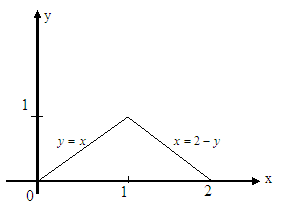
4.3 Сурет
399.
интегралын есептеу керек, мұндағы
денесі
теңсіздіктерімен анықталған. Ж:
400.
интегралын есептеу керек, мұндағы
денесі
теңсіздіктерімен анықталған. Ж:
-2,25.
401.
интегралын есептеу керек, мұндағы
денесі
теңсіздіктерімен анықталған. Ж:
402.
интегралын есептеу керек, мұндағы
денесі
жазықтықтарымен шектелген. Ж:
403.
интегралын есептеу керек, мұндағы
денесі
конустық
бетімен және
жазықтықтарымен шектелген. Ж:
2.
Үштік интегралда айнымалыларды алмастыру.
Үштік
интегралда
координаталарынан
формулаларының көмегімен
координатасына көшу
формуласымен жүзеге асады, мұндағы
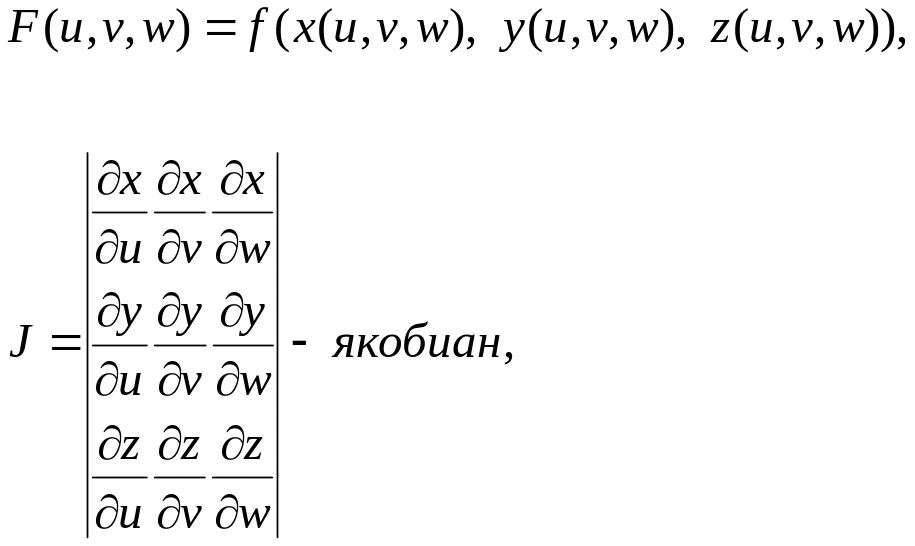
ал
-
үш өлшемді
аймағында үзіліссіз, әрі үзіліссіз
бірінші ретті дербес туындылары бар
функциялар.
Дербес жағдайда тікбұрышты координаттардан
формулаларының
көмегімен
цилиндрлік координаттарға көшкенде
якобиан
болады (4.4 Сурет). Сондықтан
