3.10 Сурет
Сондықтан
,
ал интегралдау
облысы
теңсіздіктерімен шектелген (3.11 Сурет).
Сонымен
▲
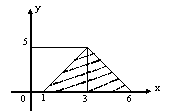
3.11 Сурет
371.
параболоиды және
жазықтығымен шектелген дененің көлемін
табу керек (3.12 Сурет).
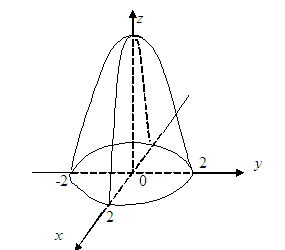
3.12 Сурет
Шешуі.
Жоғарыдан
параболоидымен, төменнен
жазықтығымен шектелген дененің көлемі
Интегралымен
анықталады, мұндағы
облысы
шеңберімен шектелген. Бұл жағдайда
формулаларының көмегімен полярлық
координаттар жүйесіне көшеміз.
болғандықтан
▲
Берілген беттермен шектелген денелердің көлемдерін табу керек:
372.
(бірінші октантта орналасқан). Ж:
12.
373.
Ж:
374.
Ж:
24.
375.
(бірінші октантта орналасқан).
Ж:
376.
Ж:
3. Беттің ауданын есептеу. Егер бет теңдеуімен берілсе, онда оның ауданы
формуласымен анықталады, мұндағы облысы берілген беттің Оху жазықтығындағы проекциясы.
Егер
бет
теңдеуімен берілсе, онда оның ауданы
формуласымен
анықталады, мұндағы
облысы берілген беттің
жазықтығындағы проекциясы.
Егер
бет
теңдеуімен берілсе, онда оның ауданы
формуласымен
анықталады, мұндағы
облысы берілген беттің
жазықтығындағы проекциясы.
377.
сферасының
цилиндрінің ішіндегі бөлігінің бетінің
ауданын табу керек
(3.13 Сурет).
Шешуі. Сфера теңдеуінен
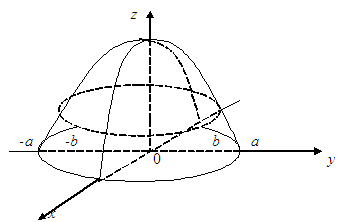
3.13 Сурет
Интегралдау
облысы
дөңгелегі болады. Осыдан
Полярлық
координаттар жүйесіне көшсек, онда
дөңгелектің теңдеуі
болғандықтан
.
▲
378.
конусының
цилиндрінің ішіндегі бөлігінің бетінің
ауданын табу керек. Ж:
379.
параболоидының
цилиндрімен қиғандағы бөлігінің бетінің
ауданын табу керек. Ж:
380.
жазықтығының координат жазықтықтарымен
шектелген бөлігінің ауданын табу
керек. Ж:
381.
цилиндрін
жазықтықтарымен қиғандағы бөлігінің
ауданын табу керек
Ж:
382.
бетін
жазықтықтарымен қиғандағы бөлігінің
ауданын табу керек. Ж:
4. Қос
интегралдың механикада қолдануы.
жазықтығында аумағы
облысы,
ал тығыздығы
болатын пластинаның массасы:
Ох және Оу осьтеріне қарағандағы статикалық моменттері:
формулаларымен анықталады.
Пластинаның
ауырлық
центрінің координаттары
формулаларымен анықталады.
Ох, Оу осьтеріне және координата бас нүктесіне қарағандағы инерция моменттері
формулаларымен анықталады.
Ескерту:
Біртекті пластина үшін
,
сондықтан
деп
алуға болады.
383.
эллипсін
түзуімен қиғанда пайда болатын сегменттің
ауырлық центрін табу керек
(3.14 Сурет).
Шешуі.
▲
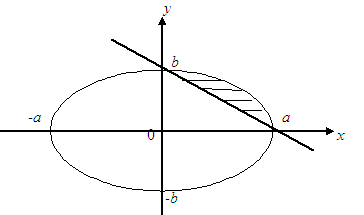
3.14 Сурет
384.
сызықтарымен шектелген пластинаның
Ох, Оу
остеріне, координаттар жүйесінің бас
нүктесіне қарағанда инерция моменттерін
табу керек
(3.15 Сурет).
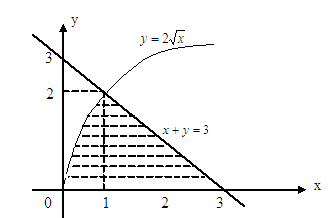
3.15 Сурет
Шешуі.
▲
385. Тығыздығы
тең
түзулерімен шектелген үшбұрышты түрде
берілген пластинаның массасын, статикалық
моменттерін, ауырлық центрін табу керек.
Ж:
386.
параболаларымен шектелген біртекті
пішіннің ауырлық центрін табу
керек. Ж: 0,4.
387.
сызықтарымен шектелген біртекті пішіннің
ауырлық центрін табу керек. Ж:
388.
параболасымен және
түзуінің қиылысынан пайда болған
біртекті пішіннің ауырлық центрін табу
керек. Ж:
389.
шеңберімен және
түзуімен шектелген біртекті пішіннің
ауырлық центрін табу керек. Ж:
390.
кардиоидасымен шектелген біртекті
пішіннің ауырлық центрін табу
керек. Ж:
391.
түзулерімен шектелген біртекті пішіннің
осьтеріне және координаттар жүйесінің
бас нүктесіне қарағандағы инерция
моменттерін есептеу керек. Ж:
392.
шеңберімен шектелген біртекті сақинаның
осьтеріне және координаттар жүйесінің
бас нүктесіне қарағандағы инерция
моменттерін есептеу керек.
Ж:
393.
параболасымен,
түзуімен шектелген біртекті пішіннің
остеріне және координаттар жүйесінің
бас нүктесіне қарағандағы инерция
моменттерін есептеу керек. Ж:
394.
кардиоидасының
осьтеріне және координаттар жүйесінің
бас нүктесіне қарағандағы инерция
моменттерін есептеу керек. Ж:
