3.7 Сурет
349.
Полярлық координаталар жүйесіне көшу
арқылы
интегралын есептеу керек, мұндағы D
облысы
шеңберімен шектелген
Шешуі.
D
облысы
радиусы
тең, центрі
болатын дөңгелек болғандықтан полярлық
координаталарға көшеміз.
шеңбері полярлық координаттар жүйесінде
формуласы арқылы анықталады.
болғандықтан
▲
350.
интегралын есептеу керек, мұндағы
облысы
шеңберлерімен шектелген.
Шешуі.
облысы радиустары
ке
және
-ге
тең, ал центрлері координаттар жүйесінің
бас нүктесі болатын екі шеңбердің
арасындағы сақина болғандықтан полярлық
координаттарға көшеміз. Бұл шеңберлер
полярлық координаттар жүйесінде
және
формулалары арқылы анықталады. Сондықтан
болғандықтан
▲
351.
интегралын есептеу керек, мұндағы
облысы
эллипсімен шектелген.
Шешуі.
деп алсақ, онда
эллипсінің полярлық координаттар
жүйесіндегі теңдеуі
Якобиан
ал
болғандықтан
▲
352.
интегралын есептеу керек, мұндағы
облысы
түзулермен шектелген.
Шешуі.
немесе
деп алсақ, онда
ал
якобиан
болады.
Сонымен
▲
Полярлық координаттарға көшу арқылы қос интегралды есептеу керек:
353.
мұндағы
облысы
шеңберімен шектелген. Ж:
354.
мұндағы
облысы
дөңгелегінің бірінші ширегі. Ж:
355.
мұндағы
облысы
және
шеңберлерімен шектелген. Ж:
356.
мұндағы
облысы
жарты шеңберімен, ОХ осімен шектелген
. Ж:
357.
интегралын есептеу керек, мұндағы
облысы
пен
және
мен
гиперболасымен шектелген.
Ж:
Ескерту.
3.3 Қос интегралдың қолданылуы
1. Жазық фигуралардың аудандарын есептеу. облысымен шектелген жазық фигураның ауданы
формуласымен анықталады.
Егер
облысы
теңсіздіктерімен шектелсе, онда
Егер
облысы полярлық координаттар жүйесінде
теңсіздіктермен шектелсе, онда
358.
және
сызықтармен шектелген жазық фигураның
ауданын табу керек.
Шешуі. Берілген сызықтардың қиылысу нүктелерін табамыз
Олар
және
нүктелері (3.8 Сурет). Сонымен
болғандықтан
▲
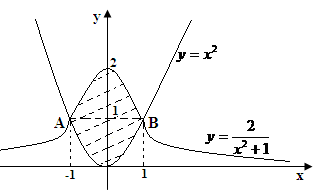
3.8 Сурет
359.
Полярлық координаттар жүйесіне көшу
арқылы
қисық сызығымен шектелген жазық фигураның
ауданын табу керек
.
Шешуі.
формулалары арқылы полярлық координаттар
жүйесіне көшсек
немесе
мұндағы
болғандықтан
Яғни
0-ден
ке
дейін өзгеретіндегі фигураның ауданы
берілген фигураның ауданының жартысына
тең болады (3.9 Сурет).
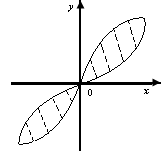
3.9 Сурет
Сонымен
▲
Берілген сызықтармен шектелген жазық фигуралардың аудандарын табу керек.
360.
Ж:
361.
Ж:
362.
Ж:
363.
Ж:
364.
(эллипс). Ж:
365.
Ж:
366.
Ж: 
367.
Ж:
368.
Ж:
369.
Ж:
2.
Денелердің көлемдерін есептеу. Жоғарыдан
бетімен, төменнен
жазықтығымен, бүйір жағынан
облысының шекарасы арқылы өтетін OZ
осіне
параллель болатын цилиндр бетімен
шектелген дененің көлемі
формуласымен есептеледі.
370.
бетімен,
,
жазықтықтарымен шектелген дененің
көлемін табу керек.
Шешуі.
Берілген дене жоғарыдан
бетімен, төменнен
жазықтығымен, ал бүйір жағынан
және
жазықтықтарымен шектелген (3.10 Сурет).
