12. Введення до оцінки складності алгоритмів

Одну і ту ж задачу можна вирішити багатьма способами, відповідно, може бути багато алгоритмів, які приводять до однакового результату за умов однакових вихідних даних.

Що може бути мірою якості алгоритму? Як один алгоритм можна вважати кращим за інший?

Складність – одна із характеристик алгоритму.

Який із алгоритмів кращий: простіший, чи складніший?

Нехай А — алгоритм розв'язання деякого класу задач, а N — розмірність окремої задачі цього класу. N може бути, наприклад, розмірністю оброблюваного масиву, числом вершин оброблюваного графа тощо,

Позначимо функцію fA(N), що дає верхню межу максимального числа основних операцій (додавання, множення і т. д.), які повинен виконати алгоритм А, розв'язуючи задачу розмірності N.

Тоді алгоритм А є поліноміальним, якщо fA(N) зростає не швидше, ніж деякий поліном від N. В іншому разі А — експоненціальний алгоритм.

Приклад: функції типу kn, kn², kn³,…, де k – коефіцієнт – поліноміальні; а функції виду kⁿ, nⁿ, n!.. - експоненціальні

У випадку традиційної Машини Т’юринга, яка ще має назву детермінованої (ДМТ), запис на стрічку, перехід каретки і зміна стану відбуваються однозначно визначено в залежності від стану машини і зчитаного нею символу.

У випадку недетермінованої Машини Т’юринга (НМТ) комбінація поточного стану машини та зчитаного символу на стрічці можуть допускати декілька переходів. Наприклад, якщо НМТ знаходиться у деякому стані 1 і зчитує символ “X”, то вона може як записати на стрічку символ Z і перейти в стан 2, так і записати на стрічку символ Y і перейти в стан 3.

Яким чином можна уявити НМТ? Існує два варіанти:

• Можна допустити, що НМТ є “виключно вдалою” і вона завжди обирає той перехід, який приводить до вирішення задачі.

• Можна уявити, що у випадку недетермінованого переходу (коли комбінація символу на стрічці і стану НМТ допускають декілька переходів) створюється копія машини (чи декілька копій, в залежності від кількості переходів), які далі функціонують паралельно.

Якщо ДМТ має єдиний шлях обчислень, то НМТ має “дерево обчислень”.

Алгоритми, складність яких є експоненціальною для ДМТ можуть мати поліноміальну складність для НМТ.

За своїми обчислювальними можливостями (здатністю вирішувати задачі) ДМТ і НМТ є еквівалентними.

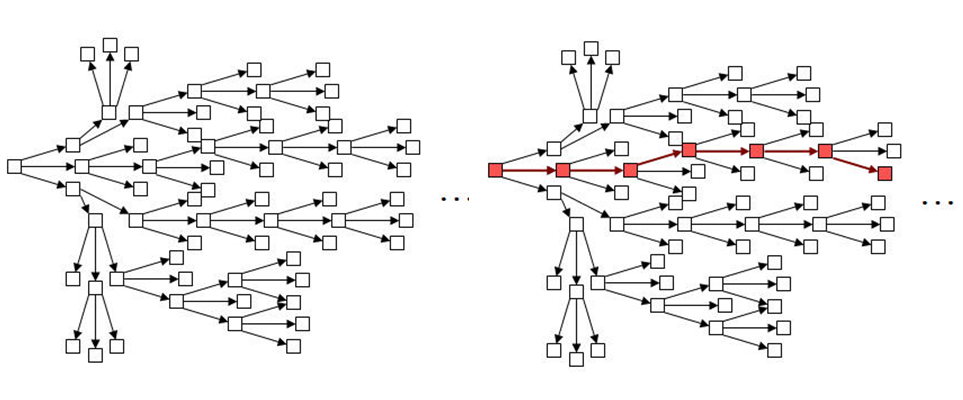
Рисунок 1.1 – Представлення НМТ у вигляді дерева варіантів

13. Визначення порядку складності алгоритму

До класу складності P належать задачі, які вирішуються за поліноміальний час за допомогою ДМТ

Що означає, що для стрічки ДМТ, у якій заповнено N комірок, необхідно здійснити не більше ніж T(N) переходів, де T(N) – деякий поліном від N

Згідно з О-нотацією, наступні задачі відносяться до класу складності P:

• Фіксований час: O(1)

• Лінійний час: O(N)

• Час за ступенем Y: O(N^Y)

• Логарифмічний час: О(log N)

Клас складності алгоритмів NP визначається аналогічно до P, але для НМТ:

До класу складності NP належать задачі, які вирішуються за поліноміальний час за допомогою НМТ

Згідно з О-нотацією, наступні задачі відносяться до класу складності NP:

• Експоненціальний час: O(Y^N)

• Час обчислення факторіалу: O(N!)

Задача перевірки, чи є число N розрядністю b складеним, НМТ вирішує за допомогою наступного алгоритму:

• 1. Обрати недетерміновано ціле число m, 1<m<N

• 2. Поділити націло N на m, залишок позначити через a

• 3. Якщо a=0, то повернути результат “ТАК”, інакше повернути “НІ”

Для наведеного алгоритму визначною частиною є час виконання ділення, який є поліноміальним – необхідно O(b²) кроків

Якщо для вирішення цієї задачі використовується ДМТ, то алгоритм слід модифікувати наступним чином:

• Від m := 2, доки m<N:

  • Поділити націло N на m, залишок позначити через a

  • Якщо a=0, то повернути результат “ТАК” і закінчити виконання, інакше m := m + 1

Як можна побачити, алгоритм для ДМТ буде експоненціальним, оскільки необхідно O(b²2^b) кроків

14. О-нотація для оцінки складності алгоритмів.

15. Фіксований час О(1).

16. Лінійний час О(N).

17. Квадратичний час О(N2).

18. Логарифмічний час О(log N) та О(N log N).

19. Час факторіалу О(N!).

Для позначення складності виконується так звана О-нотація (від англ. «order» – порядок), згідно з якою алгоритми бувають різного порядку складності:

• О(1) – алгоритм першого порядку складності – завжди займає один і той самий час на виконання;

• О(N) – алгоритм N-ного порядку складності – час зростає лінійно, пропорційно до N;

• O(N²) – алгоритм порядку складності N² – час зростає квадратично;

• O(log N) – алгоритм логарифмічного порядку складності – час зростає логарифмічно;

• O(N log N) – логарифмічно за певною основою;

• O(N!) – алгоритм порядку складності N! – час зростає у факторіальній залежності.

На рис. 1.2 подано схематичне зображення різних порядків складності.

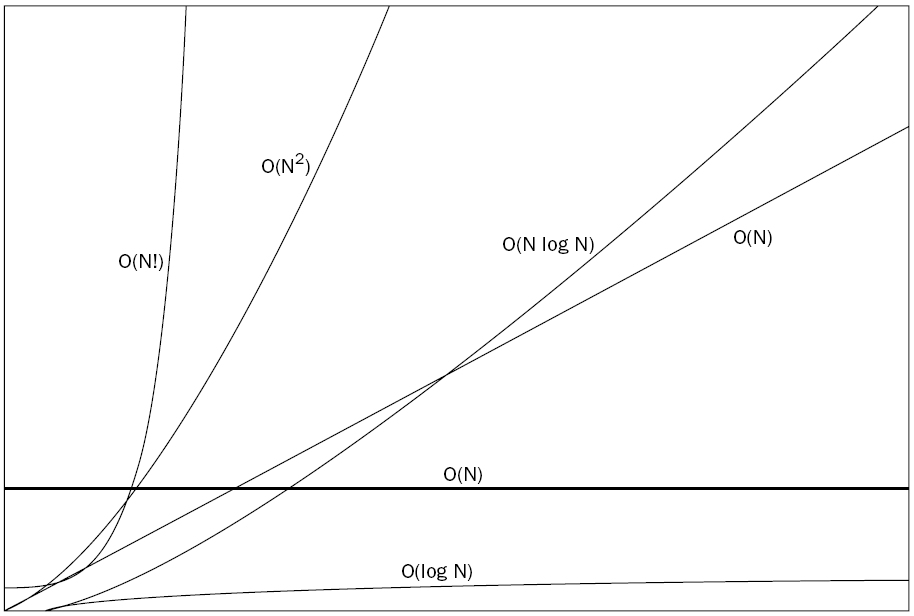
Рисунок 1.2 – Схематичне представлення різних порядків складності алгоритмів

Для деяких алгоритмів порядок складності не є фіксованим і залежить від значень вихідних даних, у такому разі можна визначити найгірший і найкращий випадки, кожен із яких може мати своє значення порядку складності.

При оцінці складності приймаються саме елементарні операції, наприклад, операція додавання є елементарною, а от операція визначення факторіалу – ні. Крім того, складність може визначатися не лише за обчислювальними ресурсами, а, наприклад, за обсягом пам’яті, яка необхідна алгоритму для його виконання.