Арифметика великих чисел
Сучасні ЕОМ працюють з числами обмеженої точності і діапазону значень, які вони можуть приймати. Наприклад, здійснити точний розрахунок 40! уже неможливо, якщо розрахунок здійснюється з використанням стандартних типів даних.
Рисунок 9.2 – Результат розрахунку факторіалу
Вирішення проблеми полягає у використанні так званої “арифметики довільної точності”, що основана на “великих числах”, які обмежуються не розрядністю ЕОМ, а обсягами доступної пам’яті
Крім того, якщо для представлення дійсних чисел використовується плаваюча кома, то під “великими числами” розуміють, насамперед великі цілі числа (big integers).
Існує група задач, що вимагають використання чисел, розрядність яких перевищує стандартні типи даних ЕОМ:
Цілочисельні розрахунки з використанням функцій, результат яких швидко зростає (факторіал, числа Фібоначчі і т.д.)
Точні наукові розрахунки
Криптографічні алгоритми
В окремих ситуаціях, навіть під час використання досить типових прикладних алгоритмів, можливе переповнення типів данних у результаті виконання операцій множення, підведення до ступеня і т.д. У такому разі, якщо оптимізацією порядку розрахунків вирішити проблему не вдається, то слід використовувати великі числа
Оскільки для великих чисел розрядність заздалегідь не визначена (вона може змінюватись у широкому діапазоні в залежності від задачі та вхідних даних), то для їх зберігання використовуються динамічні структури даних, насамперед, масиви
Зберігання великих чисел у масиві передбачає зберігання кожної окремої цифри числа (часто з цією метою використовуються масиви символів або байтів).
У чому проблема використання байтів для представлення великих чисел у десятковій системі числення?
Проблема нераціональності використання простору: один байт – 256 можливих значень, число у десятковій формі – 10 можливих значень.
Зайві витрати простору: (256-10)/256*100% = 99,7% (!!!)
Якщо використовується 32-бітний тип даних, то витрати пам’яті становлять (65536 – 10) / 65536 * 100% = 99,98% (!!!)
Яким чином можна вирішити проблему?
Реалізація великих чисел
Масив:
int[] digit = new int[10000];
Приклад програми розрахунку факторіалу довільної розмірності:
static void Main(string[] args)
{
const int Limit = 1000;
const int Base = 10;
int[] digit = new int[Limit+1];
int carry, d;
int last;
char[] text = new char[Limit+1];
char[] tdigit = new char[] { '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' };
digit[1] = 1;
last = 1;
for (int n = 1; n <= 365; n++)
{
carry = 0;
for (int i = 1; i <= last; i++)
{
d = digit[i] * n + carry;
digit[i] = d % Base;
carry = d / Base;
}
while (carry > 0)
{
if (last >= Limit)
throw new Exception("Overflow!");
last++;
digit[last] = carry % Base;
carry = carry / Base;
}
}
for (int i = 1; i <= last; i++)
{
text[Limit - i + 1] = tdigit[digit[i]];
}
string s = new String(text);
s = s.TrimStart('\0');
Console.WriteLine(s);
}
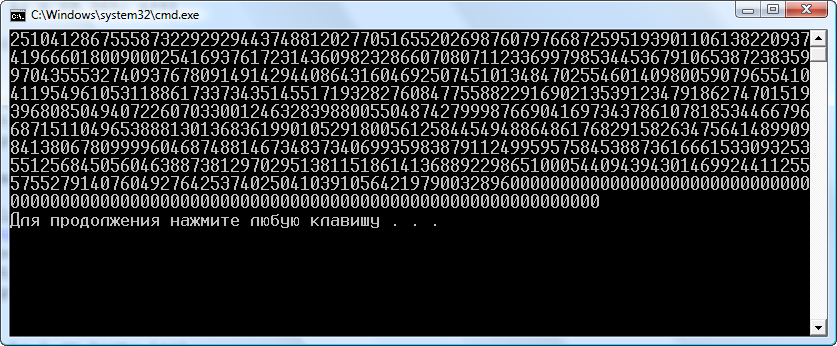
Рисунок 9.4 - Розрахунок для n = 365