Форма Бекуса-Наура для запису регулярних виразів
Форма Бекуса-Наура (БНФ) – формальна система для опису синтаксису.
Часто використовується для запису регулярних виразів. Приклад:
Синтаксичний аналіз регулярних виразів
Використання регулярних виразів здійснюється у три етапи: синтаксичний аналіз; компіляція; використання для перевірки відповідності рядкам вхідних даних.
Синтаксичний аналіз – процес перевірки відповідності наведеного синтаксису граматичним правилам.
Процес синтаксичного аналізу також має назву “парсинг” (parsing). Для синтаксичного аналізу регулярних виразів, як правило, будується нисхідний синтаксичний аналізатор (top down parser).
Компіляція регулярних виразів
Компіляція регулярного виразу – перетворення його на недетермінований кінцевий автомат.
Приклад компіляці для виразу “(a|b)*bc” (повторення нуль чи більше раз символу а чи b, за якими йдуть символи b та c).
Інструменти для спрощення роботи з регулярними виразами
Regulator - безкоштовний інструмент для побудови та перевірки регулярних виразів
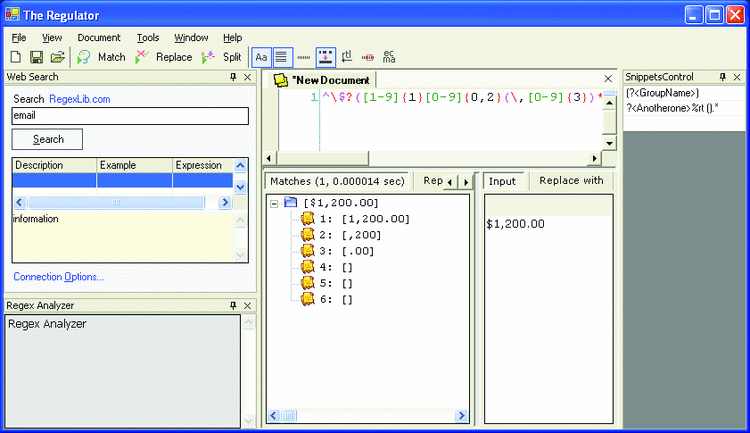
Рисунок 8.4 – Графічний інтерфейс програми Regulator
Зіставлення рядків з регулярними виразами.
В процесі зіставлення рядку з регулярним виразом відбувається виконання скомпільованого кінцевого автомату над вхідним рядком.
Приклад реалізації регулярного виразу в C# (пошук у файлі коректних адрес електронної пошти).
12. Використання регулярних виразів для автоматизації типових задач.
Приклад регулярного виразу для заміни дати формату мм/дд/рр на формат дд/мм/рр
using System;
using System.Globalization;
using System.Text.RegularExpressions;
public class Class1
{
public static void Main()
{
string dateString = DateTime.Today.ToString("d",
DateTimeFormatInfo.InvariantInfo);
string resultString = MDYToDMY(dateString);
Console.WriteLine("Converted {0} to {1}.", dateString, resultString);
}
static string MDYToDMY(string input)
{
return Regex.Replace(input,
"\\b(?<month>\\d{1,2})/(?<day>\\d{1,2})/(?<year>\\d{2,4})\\b",
"${day}-${month}-${year}");
}
}
Приклад видалення всіх символів із рядку, що не є буквенно-цифровими за винятком символів "@", "-" та ".“
using System;
using System.Text.RegularExpressions;
public class Example{
static string CleanInput(string strIn)
{
// Replace invalid characters with empty strings.
return Regex.Replace(strIn, @"[^\w\.@-]", "");
}
}
Алгоритми систем числення
Перелік питань:
Введення до систем числення.
Двійкова система числення.
Шістьнадцяткова система числення.
Системи числення з нетрадиційними основами.
Перетворення між різними системами числення.
Арифметика чисел з плаваючою комою.
Точність операцій з плаваючою комою.
Арифметика великих чисел.
Введення до систем числення
Система числення - сукупність прийомів та правил найменування й позначення чисел.
Позиційна - система числення, в якій значення кожної цифри залежить від місця в послідовності цифр у записі числа.
Непозиційна - система числення, в якій значення кожної цифри в довільному місці послідовності цифр, яка означає запис числа, не змінюється.
Щоб визначити число, недостатньо знати тип і алфавіт системи числення. Для цього необхідно ще додати правила, які дають змогу за значеннями цифр встановити значення числа.
Найпростішим способом запису натурального числа є зображення його за допомогою відповідної кількості паличок або рисочок. Таким способом можна користуватися для невеликих чисел.
Наступним кроком було винайдення спеціальних символів (цифр). У непозиційній системі кожен знак у запису незалежно від місця означає одне й те саме число. Добре відомим прикладом непозиційної системи числення є римська система, в якій роль цифр відіграють букви алфавіту: І - один, V - п'ять, Х - десять, С - сто, Z - п'ятдесят, D - п'ятсот, М - тисяча. Наприклад, 324 = СССХХІV. У непозиційній системі числення незручно й складно виконувати арифметичні операції.
Поширений приклад непозиційної системи числення – римська система числення, де замість цифр використовуються латинські букви (таблиця 10.1).
Таблиця 10.1 – Цифри римської системи числення
Римська цифра |
Десяткове значення |
I |
1 |
V |
5 |
X |
10 |
L |
50 |
C |
100 |
D |
500 |
M |
1000 |
Наприклад, VII = 5 + 1 + 1 = 7. Тут символи V і I означають 5 і 1, відповідно, незалежно від місця їх у числі.
Загальноприйнятою в сучасному світі є десяткова позиційна система числення, яка з Індії через арабські країни прийшла в Європу. Основою цієї системи є число десять. Основою системи числення називається число, яке означає, у скільки разів одиниця наступного розрядку більше за одиницю попереднього.
Загальновживана форма запису числа є насправді не що інше, як скорочена форма запису розкладу за степенями основи системи числення, наприклад:
130678=1*105+3*104+0*103+6*102+7*101+8
Тут 10 є основою системи числення, а показник степеня - це номер позиції цифри в записі числа (нумерація ведеться зліва на право, починаючи з нуля). Арифметичні операції у цій системі виконують за правилами, запропонованими ще в середньовіччі. Наприклад, додаючи два багатозначних числа, застосовуємо правило додавання стовпчиком. При цьому все зводиться до додавання однозначних чисел.