6. Визначення дерева

Дерево - одна з найпоширеніших структур даних. Формально дерево визначається як скінченна множина Т з однієї або більше вершин (вузлів, nodes), яке задовольняє наступним вимогам:

1. існує один виокремлений вузол - корень (root) дерева

2. інші вузли (за виключенням кореня) розподілені серед m ≥ 0 непересічних множин T₁...T_m і кожна з цих множин в свою чергу є деревом. Дерева T₁...T_m мають назву піддерев (subtrees) даного кореня.

Графічне зображення дерева представлено на рис. 7.5.

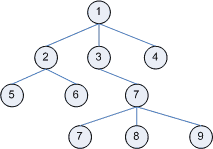
Рисунок 7.5 – Графічне зображення дерева

З цього визначення випливає, що кожна вершина є в свою чергу коренем деякого піддерева. Кількість піддерев вершини має назву ступеня (degree) цієї вершини. Вершина ступеню нуль має назву кінцевої (terminal) або листа (leaf). Некінцева вершина також має назву вершини розгалуження (branch node). Нехай x - довільна вершина дерева з коренем r. Тоді існує єдиний шлях з r до x. Усі вершини на цьому шляху називаються предками (ancestors) x; якщо деяка вершина y є предком x, то x називається нащадком (descendant) y. Нащадки та предки вершини x, що не співпадають з нею самою, називаються власними нащадками та предками. Кожну вершину x, в свою чергу, можна розглядати як корень деякого піддерево, елементами якого є вершини-нащадки x. Якщо вершини x є предком y та не існує вершин поміж ними (тобто x та y з'єднані одним ребром), а також існують предки для x (тобто x не є коренем), то вершина x називається батьком (parent) до y, а y - дитиною (child) x. Коренева вершина єдина не має батьків. Вершини, що мають спільного батька, називаються братами (siblings). Вершини, що мають дітей, називаються внутрішніми (internal). Глибиною вершини x називається довжина шляху від кореня до цієї вершини. Максимальна глибина вершин дерева називається висотою.

Лісом (forest) називають множину дерев, які не перетинаються.

Найчастіше дерева в інформатиці зображують з коренем, який знаходиться зверху (говорять, що дерево в інформатиці "росте вниз").

Важливими операціями на деревах є:

• обхід вершин в різному порядку;

• перенумерація вершин;

• пошук елемента;

• додавання елемента у визначене місце в дереві;

• видалення елемента;

• видалення цілого фрагмента дерева;

• додавання цілого фрагмента дерева;

• трансформації (повороти) фрагментів дерева;

• знаходження кореня для будь-якої вершини.

Найбільшого розповсюдження ці структури даних набули в тих задачах, де необхідне маніпулювання з ієрархічними даними, ефективний пошук в даних, їхнє структуроване зберігання та модифікація.

Існують різні сфери використання та способи представлення дерев.

Графічне представлення дерева у вигляді множини представлено на рисунку 7.6.

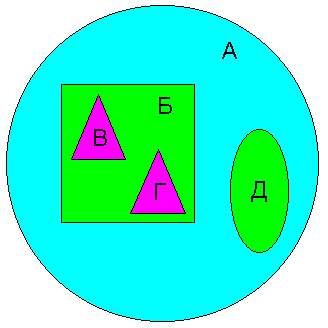
Рисунок 7.6 – Графічне представлення дерева у вигляді множини

Більш формально представлення дерева у вигляді множини можна сприймати наступним чином: вершина Б є дочірньою по відношенню до вершини А в тому разі, якщо діапазон чисел вершини Б лежить всередині діапазону вершини А.

Представлення дерева у вигляді вкладених дужок:

(V0(V1(V2(V5)(V6))(V3)(V4))(V7(V8)(V9(V10))))

Представлення дерева у вигляді графа (рисунок 7.7).

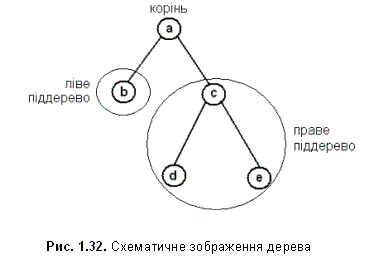
Рисунок 7.7 – Представлення дерева у вигляді графа

Представлення дерева у вигляді списку з уступами (рисунок 7.8).

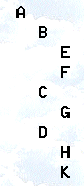
Рисунок 7.8 – Представлення дерева у вигляді списку з уступами

Представлення дерева у вигляді десяткової системи Д’юі (рисунок 7.9)

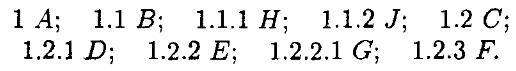
Рисунок 7.9 – Представлення дерева у вигляді десяткової системи Д’юі

Представлення дерева у вигляді діаграми Венна (рисунок 7.10)

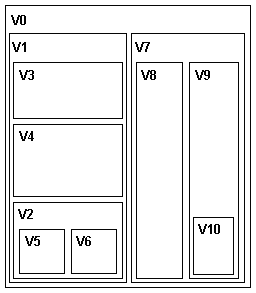
Рисунок 7.10 – Представлення дерева у вигляді діаграми Венна

Обхід дерева

Обхід дерева – одна з найпоширеніших операцій з деревами.

Передбачає відвідування усіх вершин дерева, при цьому кожна вершина відвідується один раз.

Існують різні способи здійснення обходу дерева: обхід у глибину з використанням рекурсії, обхід у глибину без використання рекурсії, обхід у ширину та ін.