Упорядкування масивів: сортування вибором; сортування вставкою; бульбашкове сортування; сортування методом Шелла; метод швидкого сортування.
Сортування – процес перестановки об’єктів у певному порядку.
Основне призначення сортування – полегшення пошуку об’єктів.
Існує велика кількість алгоритмів сортування, одного «найкращого» до нинішнього часу не винайдено. Вибір підходящого алгоритму залежить від характеру даних, їх розподілу, пам’яті, у якій вони зберігаються.
Наприклад, поширеним є поділ алгоритмів сортування на:
внутрішні – сортування масивів і даних в оперативній пам’яті;
зовнішні – сортування даних у файлах.
На рис. 6.1 умовно представлено сортування масиву, на рис. 6.2 – сортування файлу.
Рисунок 6.1 – Сортування масиву
Рисунок 6.2 – Сортування файлу
За зміною порядку елементів розрізняють:
стійке сортування – при виконанні алгоритму на відсортованому наборі даних порядок елементів не змінюється;
нестійке сортування – при виконанні алгоритму на відсортованому наборі даних порядок елементів змінюється.
Ключ – елемент даних, за яким здійснюється сортування. Для ключа має використовуватися такий тип даних, для якого існує спосіб визначення порядку елементів.
Складність виконання алгоритму – кількість операцій, а також обсяг додаткової пам’яті, необхідної для його виконання.
Найпростіший алгоритм сортування водночас є неефективним (нерозумним), його складність О(n3):
using System;
using System.Collections.Generic;
using System.Text;
namespace SortApplication
{
class Program
{
static void swap(int[] arr, int i, int j)
{
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
static void stupidSort(int[] arr)
{
int i = 0;
while (i < arr.Length - 1)
{
if (arr[i + 1] < arr[i])
{
swap(arr, i, i + 1);
i = 0;
}
else
{
i++;
}
}
}
static void Main(string[] args)
{
int[] testArr = { 44, 55, 12, 42, 94, 18, 06, 67};
stupidSort(testArr);
foreach (int i in testArr)
{
Console.Write("{0} ", i);
}
Console.ReadLine();
}
}
}
Інший варіант нерозумного сортування – сортування Акульшина: генеруються всі можливі перестановки масиву, для яких здійснється перевірка правильного порядку. Складність: О (n × n!).
Алгоритм сортування вставками
Основна ідея алгоритму полягає в тому, щоб поступово впорядковувати масив, вставляючи нові елементи у вже впорядковану частину (рис. 6.3). Складність алгоритму – О (n2).
Рисунок 6.3 – Схематичне представлення роботи алгоритму сортування простими вставками
Код програми:
using System;
using System.Collections.Generic;
using System.Text;
namespace SortingApplication
{
class Program
{
static void insertSort(int[] a)
{
int i, j, value;
for (i = 1; i < a.Length ; i++)
{
value = a[i];
for (j = i - 1; (j >= 0) && (a[j] > value); j--)
{
a[j + 1] = a[j];
}
a[j + 1] = value;
}
}
static void Main(string[] args)
{
int[] testArr = {44, 55, 12, 42, 94, 18, 06, 67};
insertSort(testArr);
foreach (int i in testArr)
{
Console.Write("{0} ", i);
}
Console.ReadLine();
}
}
}
Результат виконання програми (рис. 6.4).
Рисунок 6.4 – Результат виконання програми
Особливості алгоритму – простий і наглядний в реалізації, однак ресурсоємний.
Модифікований варіант даного алгоритму – сортування бінарними вставками оснований на тому, що у вже відсортованій частині масиву елементи можна включати, виконуючи бінарний пошук.
Алгоритм бульбашкового сортування
Алгоритм бульбашкового сортування передбачає повторні проходи по масиву, який сортується. За кожен прохід елементи порівнюються попарно і якщо порядок серед двох елементів невірний, то здійснюється обмін елементів. Проходи по масиву виконуються до тих пір, доки не стане зрозуміло, що обміни елементів вже не потрібні, тобто масив відсортований.
Свою назву алгоритм отримав за принципом роботи – у процесі його виконання елемент, який стоїть не на власному місці, «спливає» до необхідної позиції наче бульбашка у воді.
Схематично робота алгоритму представлена на рис. 11.3.
Складність алгоритму – О(n2).
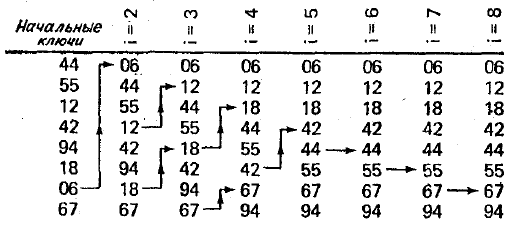
Рисунок 6.5 – Схематичне представлення роботи алгоритму бульбашкового сортування
Код програми, яка виконує бульбашкове сортування:
using System;
using System.Collections.Generic;
using System.Text;
namespace SortApplication
{
class Program
{
static void swap(int[] arr, int i, int j)
{
int t = arr[i];
arr[i] = arr[j];
arr[j] = t;
}
static void bubbleSort(int[] arr)
{
for (int i = arr.Length - 1; i > 0; i--)
{
for (int j = 0; j < i; j++)
{
if (arr[j] > arr[j + 1])
{
swap(arr, j, j + 1);
}
}
}
}
static void Main(string[] args)
{
int[] testArr = {44, 55, 12, 42, 94, 18, 06, 67};
bubbleSort(testArr);
foreach (int i in testArr)
{
Console.Write("{0} ", i);
}
Console.ReadLine();
}
}
}
Модифікації алгоритму:
виявлення проведених обмінів;
шейкер-сортування.
Алгоритм сортування за методом Шелла
Ідея алгоритму – необхідно порівнювати елементи, які знаходяться не тільки поряд, а і на відстані один від одного. Спочатку порівнюються і сортуються між собою ключі, які стоять на певній відстані d. Після цього процедура повторюється для деяких менших значень d, і так до тих пір, доки d не стане рівним одному, у такому разі робота методу буде ідентична сортуванню простими вставками.
Схематично робота алгоритму представлена на рис. 6.6.
Складність алгоритму: O(n log n)
Рисунок 6.6 – Схематичне представлення роботи алгоритму
Код програми:
using System;
using System.Collections.Generic;
using System.Text;
namespace SortApplication
{
class Program
{
static void shellSort(int[] arr)
{
int j;
int step = arr.Length / 2;
while (step > 0)
{
for (int i = 0; i < (arr.Length - step); i++)
{
j = i;
while ((j >= 0) && (arr[j] > arr[j + step]))
{
int tmp = arr[j];
arr[j] = arr[j + step];
arr[j + step] = tmp;
j--;
}
}
step = step / 2;
}
}
static void Main(string[] args)
{
int[] testArr = {44, 55, 12, 42, 94, 18, 06, 67};
shellSort(testArr);
foreach (int i in testArr)
{
Console.Write("{0} ", i);
}
Console.ReadLine();
}
}
}
Особливості алгоритму – за звичайних обставин кількість порівнянь є меншою, ніж у алгоритмів сортування вставками та бульбашкового сортування.
Алгоритм швидкого сортування
Алгоритм швидкого сортування або алгоритм сортування Хоара – найшвидший серед відомих алгоритмів сортування загального призначення. Розроблений англійським інформатиком Чарльзом Хоаром. Швидшими за нього є лише спеціалізовані алгоритми, які побудовані з урахуванням специфіки даних, для яких вони використовуються.
Ідея алгоритму основана на принципі «поділяй і володарюй»:
Обираємо деякий елемент, який буде називатися опорним елементом.
Здійснюємо операцію поділу масиву: реорганізуємо його таким чином, щоб всі елементи менші чи рівні опорному були зліва від нього, а всі більші – справа.
Рекурсивно за цим же алгоритмом впорядковуємо списки елементів, які знаходяться зліва і справа від опорного.
Складність алгоритму: в середньому – О(n log n), найгірший випадок – О (n2).
Код програми:
using System;
using System.Collections.Generic;
using System.Text;
namespace SortApplication
{
class Quicksort
{
public static void qsort(int[] items)
{
qs(items, 0, items.Length - 1);
}
static void qs(int[] items, int left, int right)
{
int i, j;
int x, y;
i = left; j = right;
x = items[(left + right) / 2];
do
{
while ((items[i] < x) && (i < right))
{
i++;
}
while ((x < items[j]) && (j > left))
{
j--;
}
if (i <= j)
{
y = items[i];
items[i] = items[j];
items[j] = y;
i++; j--;
}
} while (i <= j);
if (left < j)
{
qs(items, left, j);
}
if (i < right)
{
qs(items, i, right);
}
}
}
class Program
{
static void Main(string[] args)
{
int[] testArr = {44, 55, 12, 42, 94, 18, 06, 67};
Quicksort.qsort(testArr);
foreach (int i in testArr)
{
Console.Write("{0} ", i);
}
Console.ReadLine();
}
}