Пошук екстремуму функцій одної змінної: метод золотого перетину; метод парабол.
Припустимо, що нам задано інтервал, на якому слід здійснити пошук мінімуму функції. Розмістимо на цьому інтервалі дві точки симетрично до його центру і здійснено обчислення функції у них:
Рисунок 5.1 – Золотий перетин
Якщо f(x1) < f(x2), то права частина вилучається і мінімум слід шукати на лівій частині інтервалу:
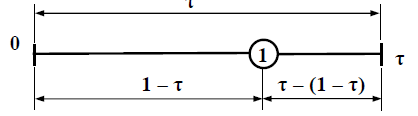
Рисунок 5.2 – Пошук на лівій частині інтервалу
Оскільки одна точка і обчислене значення вже є, то на відрізку слід встановити наступну точку (також симетрично) і повторити ітерацію:
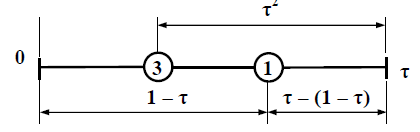
Рисунок 5.3 – Повторення ітерації
Визначення координат кожної наступної точки здійснюється, виходячи із наступного співвідношення: τ / 1 = (1 – τ) / τ, звідки випливає, що 1 – τ = τ2 Далі можна визначити τ = (-1 ± √5)/2, позитивне значення: τ = 0,61803…
Таким чином використовуючи значення τ, або (1 – τ), помножене на довжину інтервалу, можна визначити координати наступної точки.
Назву цей метод отримав із-за принципом поділу інтервалу який має назву “золотий перетин” і часто використовується у мистецтві, архітектурі і т.д.
Метод парабол
Метод парабол дозволяє апроксимувати функцію поліномом і отримати краще наближення до значення екстремуму.
Опис алгоритму:
Обираємо на досліджуваному інтервалі три точки u1, u2, u3, такі, що u1 < u2 < u3
Будуємо параболу: Q(u) = a0 + a1 (u - u1) + a2 (u - u1)(u - u2), графік якої проходить через точки (u1,f(u1)), (u2,f(u2)), (u3,f(u3)). Коефіцієнти ak, k = 1, 2, 3 знаходяться із системи рівнянь: Q(u1) = f(u1), Q(u2) = f(u2), Q(u3) = f(u3), звідки:
Точку u мінімуму Q(u) знаходять, прирівнявши його похідну до нуля:
Отримана точка приймається за наступне наближення, інші дві точки обираються із відповідних точок інтервалу [u1, u3]
Пошук екстремуму функцій багатьох змінних: метод координатного спуску; метод найскорішого спуску.
Пошук екстремуму (мінімуму) функції багатьох змінних F( x1, x2,.., xk)за методом координатного спуску полягає у почерговому пошуку мінімуму по координаті x1, далі по координаті x2 і т.д. Пошук здійснюється з однаковим кроком, який зменшується після знаходження наближених значень по всім координатам для уточнення рішення.
У загальному випадку, для того, щоб знайти точку x* локального мінімуму функції F(x(k)), складають послідовність точок (наближених рішень) {x(k)}, яка сходиться до точки x*.
Крок обирається таким чином, щоб:
xn+1(k)=xn(k) + h (1)
при
F (xn+1(k))<F (xn(k)) (2)
та
xn+1(k)=xn(k) – h (3)
при
F (xn+1(k))>F (xn(k)) (4)
Обчислення припиняють, коли досягається задана точність: |xn+1(k) – xn(k)| < e
Для пошуку екстремуму по одній координаті використовуються ті ж методи, що й для пошуку екстремуму однієї змінної (наприклад, метод золотого перетину).
Метод найскорішого спуску (градієнтів)
Метод найскорішого спуску для пошуку мінімуму функції багатьох змінних реалізує ітераційну процедуру руху до мінімуму функції із довільно обраної точки початкового наближення у напрямку найбільш сильного зменшення функції.
Цей напрямок є протилежним вектору градієнта, який формується із похідних функції по всім її аргументам.
Приклад: вектор градієнта функції f (x, y, z) = 2x + 3y2 – sin z буде (2, 6y, -cos z)
Алгоритм:
Обчислюються складові вектору градієнту в черговій i-й точці (Xi)
Складається функція f[Xi - a grad f(Xi)] однієї змінної a.
Здійснюється пошук мінімуму f[Xi - a grad f(Xi)] → min a
Визначаються координати чергової точки:
Якщо умова зупинки (|xn+1(k) – xn(k)| < e) не виконується, то переходять на крок 1.
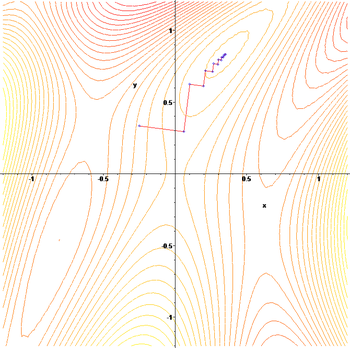
Рисунок 5.4 – Графічне представлення методу градієнтів
Приклад програмного коду: http://is.gd/b9TAi