Чисельне інтегрування: метод трапецій; метод Сімпсона; метод Сімпсона з оцінкою погрішності.
Інтеграл:
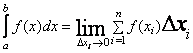
Можна
замінити:
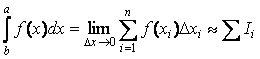
1.
Метод прямокутників: замінюємо графік
функції F(x) горизонтальною лінією,
обчислюємо інтеграл як площу прямокутників
,
де h – крок інтегрування, y0 – значення
функції при x0
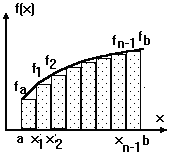
Рисунок 4.2 – Чисельне інтегрування методом прямокутників
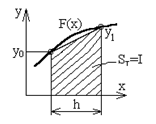
Рисунок 4.3 – Розрахунок площі прямокутника і трапеції
2.
Метод трапецій: здійснюємо аналогічну
заміну, але прямою, яка проходить через
дві точки (x0, y0) та (x0 + h, y1), обчислюємо
інтеграл як площу трапеції
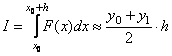
Метод Сімпсона
Замінюємо графік функції F(x) квадратичною параболою, яка проходить через три точки з координатами (х0,у0), (х0+h,у1), (х0+2h,у2). Розрахункову формулу для обчислення елементу інтегральної суми визначають, виходячи із лінійної інтерполяції:
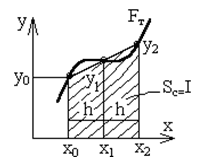
Рисунок 4.4 – Графічне представлення методу Сімпсона
Загальні функції по методам:
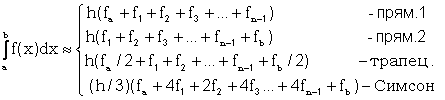
Вирішення рівнянь з одним невідомим: метод простих ітерацій; метод Ньютона; метод парабол.
Існує формула для вирішення квадратного рівняння, рівняння третього ступеня.
Як щодо рівняння четвертого ступеня? П’ятого?
Для вирішення багатьох рівнянь, аналітичне рішення яких є складним, громіздким, або взагалі неможливим, на допомогу приходять чисельні методи.
Метод простих ітерацій.
При вирішенні рівняння методом простих ітерацій використовується запис його у вигляді x = f(x). Задаються початкове значення аргументу x0 та наближення ε. Перше наближення x1 знаходиться із виразу x1 = f(x0), друге – x2 = f(x1) і т.д. У загальному випадку i+1 наближення знаходиться по формулі xi + 1 = f(xi). Зазначена процедура повторюється, доки |f(xi) > ε |. Умова сходимості метода ітерацій: |f'(x)|<1.
Опис алгоритму: доки | f(xi) > ε виконувати xi+1 =f(xi).
Алгоритми вирішення системи лінійних рівнянь, пошуку екстремуму функції
Перелік питань
Вирішення системи лінійних рівнянь методом Гауса.
Пошук екстремуму функцій одної змінної: метод золотого перетину; метод парабол.
Пошуку екстремуму функцій багатьох змінних: метод координатного спуску; метод найскорішого спуску.
Вирішення системи лінійних рівнянь методом Гауса
Представимо систему лінійних рівнянь наступним чином:
Далі, здійснюючи елементарні перетворення, приведемо матрицю до трикутного вигляду:
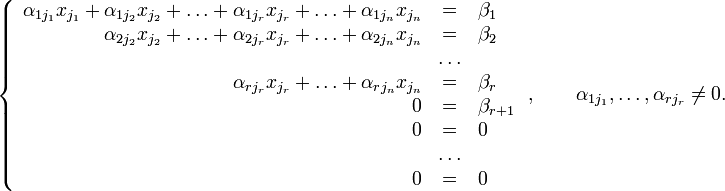
Далі, починаючи з найнижчого рівняння слід визначати корінь, підставляти його у вище рівняння і т.д. до останнього.
Процес елементарних перетворень здійснюється наступним чином: із другого рівняння віднімається перше, помножене на таке число, щоб зник коефіцієнт при x1. Потім таким же чином віднімемо перше рівняння із третього, четвертого і т.д. Тоді будуть виключені всі коефіцієнти першого стовбця, які знаходяться нижче головної діагоналі. Далі, використовуючи друге рівняння, виключаються коефіцієнти другого стовбця і т.д.
Опис алгоритму
На першому етапі (прямий хід) матрицю приводять до трикутної форми, чи визначають, що система не є сумісною. Робиться це наступним чином: серед елементів першого стовпця обирають ненульовий, переміщують його у крайнє верхнє положення перестановкою рядків і віднімають отриманий після перестановок перший рядок із інших, помножив його на величину, яка дорівнює відношенню першого елемента кожного із цих рядків до першого елемента першого рядку, обнуляючи стовбець під ним. Після того, як вказані перетворення здійснені, перший рядок і перший стовпець подумки викреслюють і продовжують до тих пір, доки не залишиться матриця нульового розміру. Якщо на якійсь з ітерацій серед елементів першого стовпця не знайшовся нульовий, то переходять до наступного.
На другому етапі (зворотній хід) слід виразити рішення системи рівнянь. Процедура починається з останнього рівняння, із якого виражають базисну змінну і підставляють у вище рівняння, піднімаючись таким чином нагору.
Приклад роботи алгоритму
Необхідно вирішити наступну систему лінійних рівнянь:
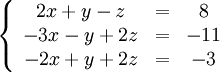
Обнулимо коефіцієнти біля x у другому та третьому рядках. Для цього помножимо перший рядок на 2/3 та 1 відповідно і складемо з першим рядком:
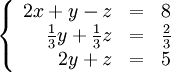
Аналогічно поступимо із коефіцієнтом при y у третьому рядку (множимо другий рядок на -6 і складаємо з третім):
Таким чином система приведена до трикутного вигляду.
На зворотньому ході вирішемо рівняння, починаючи з нижнього:
z = -1
y = 3
x = 2
Приклад коду
using System;
public class Gaussian
{
public static void Main()
{
int n = 0;
string data;
Console.WriteLine("\n****** Gaussian Eminination ******");
//input # of equations
Console.Write("Input number of euqations:");
data = Console.ReadLine();
n = int.Parse(data);
double[,] a = new double[n, n];
double[] b = new double[n];
double x, sum;
//input matrix coefficients
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
{
Console.Write("Input matrix coefficients a[" + i + "," + j + "]=");
data = Console.ReadLine();
a[i, j] = double.Parse(data);
}
//input right-hand side vector
for (int i = 0; i < n; i++)
{
Console.Write("Input right-hand side vecotr b[" + i + "]=");
data = Console.ReadLine();
b[i] = double.Parse(data);
}
Console.WriteLine("Coefficient matrix:");
printMatrix(a, n);
Console.WriteLine("\nRigh-hand side vector:");
printVector(b, n);
//convert to upper triangular form
for (int k = 0; k < n - 1; k++)
{
try
{
for (int i = k + 1; i < n; i++)
{
x = a[i, k] / a[k, k];
for (int j = k + 1; j < n; j++)
a[i, j] = a[i, j] - a[k, j] * x;
b[i] = b[i] - b[k] * x;
}
}
catch (DivideByZeroException e)
Console.WriteLine(e.Message);
}
/* back substitution */
b[n - 1] = b[n - 1] / a[n - 1, n - 1];
for (int i = n - 2; i >= 0; i--)
{
sum = b[i];
for (int j = i + 1; j < n; j++)
sum = sum - a[i, j] * b[j];
b[i] = sum / a[i, i];
}
Console.WriteLine("Solution:");
printVector(b, n);
} // Main()
public static void printMatrix(double[,] a, int n)
{
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
Console.Write(a[i, j].ToString("F4") + "\t");
Console.WriteLine();
}
Console.WriteLine();
}
public static void printVector(double[] b, int n)
{
for (int i = 0; i < n; i++)
Console.Write(b[i].ToString("F4") + "\t");
Console.WriteLine("\n");
}
}