4. Алгоритми чисельних методів, апроксимації функцій, інтегрування та вирішення рівнянь з одним невідомим

Перелік питань

1. Чисельні методи.

2. Особливості вирішення задач чисельними методами, точність та коректність рішень.

3. Апроксимації функцій: лінійна інтерполяція; інтерполяційний многочлен Ньютона.

4. Чисельне інтегрування: метод трапецій; метод Сімпсона; метод Сімпсона з оцінкою погрішності.

5. Вирішення рівнянь з одним невідомим: метод простих ітерацій; метод Ньютона; метод парабол.

1. Чисельні методи

Чисельні методи — методи наближеного або точного розв'язування задач, які ґрунтуються на побудові послідовності дій над скінченною множиною чисел.

У програмуванні та алгоритмізації чисельні методи – це математичний інструментарій, за допомогою якого математична задача формулюється у вигляді, зручному для розв’язання на комп’ютері. У такому разі говорять про перетворення математичної задачі в обчислювальну задачу. При цьому послідовність виконання необхідних арифметичних і логічних операцій визначається алгоритмом її розв’язання. Алгоритм повинен бути ітеративним (рекурсивним) і складатися з відносно невеликих блоків, які багаторазово виконуються для різних вхідних даних.

Основні риси чисельних методів:

• передбачають проведення великої кількості рутинних арифметичних обчислень за допомогою рекурсивних співвідношень, які використовуються для організації ітерацій (повторюваних циклів обчислень із зміненими початковими умовами для поліпшення результату);

• направлені на локальне спрощення задачі (наприклад, лінеаризація нелінійних обчислень);

• залежать від близкості початкового наближення

2. Особливості вирішення задач чисельними методами, точність та коректність рішень

Використання чисельних методів має певні особливості.

Зокрема, у процесі вирішення задачі виникає похибка, викликана наступними причинами:

Неточний математичний опис задачі, зокрема, вихідні дані.

Неточний метод, який використовується для задачі (використання чисельних методів само собою передбачає обмежену кількість розрахунків, а не нескінченну, яка необхідна для отримання точного результату, однак неможлива на сучасних ЕОМ).

При введенні даних і виконанні обчислень за допомогою ЕОМ відбуваються округлення.

Відповідно похибка буває:

p1 - Така, що не можна усунути:

• викликана неточністю числових даних, які входять у математичний опис задачі;

• є наслідком невідповідності математичного опису задачі реальності – похибка математичної моделі.

p2 - Похибка метода

p3 - Похибка обчислення

Повна похибка: p0 = p1 + p2 + p3.

Повна похибка визначає різницю між фактично отриманим і точним рішенням задачі.

3. Апроксимації функцій: лінійна інтерполяція; інтерполяційний многочлен Ньютона.

Апроксимація функцій – типова прикладна сфера використання чисельних методів, полягає у заміні оригінальної функції наближеною.

Потреба в апроксимації виникає найчастіше у ситуаціях, коли розрахунок оригінальної функції є трудомістким, а апроксимований (наближений) варіант є прийнятним.

Лінійна інтерполяція (метод хорд) – використовується у ситуаціях, коли функція лінійно залежить від параметрів. Полягає у інтерполяції P1(x) = ax + b функції f, що задана в двух точках x0 и x1 відрізку [a, b].

Виходячи з формули прямої:

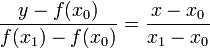
Отримаємо для

Рисунок 4.1 – Приклад кусково-лінійної інтерполяції

Приклад коду для виконання лінійної інтерполяції

static double interpolate(double x0, double y0, double x1, double y1, double x)

{

return y0 * (x - x1) / (x0 - x1) + y1 * (x - x0) / (x1 - x0);

}

Пояснення: у вигляді параметрів задаються значення двох відомих аргументів і результатів функції (відповідно x0, x1 та y0, y1), а також значення аргументу (x), для якого необхідно здійснити інтерполяцію

Інтерполяційний многочлен Ньютона

У ситуації, коли лінійна інтерполяція не дає очікуваних результатів, слід застосувати інші (нелінійні) методи, одним за найпоширеніших серед яких є інтерполяційний многочлен Ньютона.

Якщо дано k+1 точок даних: (де значення xj не повторюються)

То комбінація поліномів Ньютона буде являтися інтерполяцією функції:

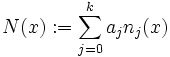
де:

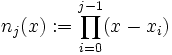
якщо